江苏省扬州市2021年中考数学试卷
试卷更新日期:2021-06-22 类型:中考真卷
一、单选题
-
1. 实数100的倒数是( )A、100 B、 C、 D、2. 把图中的纸片沿虚线折叠,可以围成一个几何体,这个几何体的名称是( )
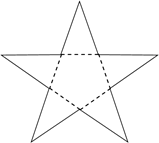 A、五棱锥 B、五棱柱 C、六棱锥 D、六棱柱3. 下列生活中的事件,属于不可能事件的是( )A、3天内将下雨 B、打开电视,正在播新闻 C、买一张电影票,座位号是偶数号 D、没有水分,种子发芽4. 不论x取何值,下列代数式的值不可能为0的是( )A、 B、 C、 D、5. 如图,点A、B、C、D、E在同一平面内,连接 、 、 、 、 ,若 ,则 ( )
A、五棱锥 B、五棱柱 C、六棱锥 D、六棱柱3. 下列生活中的事件,属于不可能事件的是( )A、3天内将下雨 B、打开电视,正在播新闻 C、买一张电影票,座位号是偶数号 D、没有水分,种子发芽4. 不论x取何值,下列代数式的值不可能为0的是( )A、 B、 C、 D、5. 如图,点A、B、C、D、E在同一平面内,连接 、 、 、 、 ,若 ,则 ( )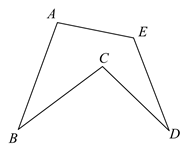 A、 B、 C、 D、6. 如图,在 的正方形网格中有两个格点A、B,连接 ,在网格中再找一个格点C,使得 是等腰直角三角形,满足条件的格点C的个数是( )
A、 B、 C、 D、6. 如图,在 的正方形网格中有两个格点A、B,连接 ,在网格中再找一个格点C,使得 是等腰直角三角形,满足条件的格点C的个数是( ) A、2 B、3 C、4 D、57. 如图,一次函数 的图像与x轴、y轴分别交于点A、B,把直线 绕点B顺时针旋转 交x轴于点C,则线段 长为( )
A、2 B、3 C、4 D、57. 如图,一次函数 的图像与x轴、y轴分别交于点A、B,把直线 绕点B顺时针旋转 交x轴于点C,则线段 长为( ) A、 B、 C、 D、8. 如图,点P是函数 的图像上一点,过点P分别作x轴和y轴的垂线,垂足分别为点A、B,交函数 的图像于点C、D,连接 、 、 、 ,其中 ,下列结论:① ;② ;③ ,其中正确的是( )
A、 B、 C、 D、8. 如图,点P是函数 的图像上一点,过点P分别作x轴和y轴的垂线,垂足分别为点A、B,交函数 的图像于点C、D,连接 、 、 、 ,其中 ,下列结论:① ;② ;③ ,其中正确的是( )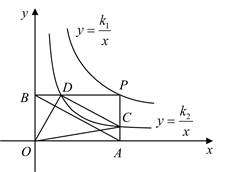 A、①② B、①③ C、②③ D、①
A、①② B、①③ C、②③ D、①二、填空题
-
9. 2021年扬州世界园艺博览会以“绿色城市,健康生活”为主题,在某搜索引擎中输入“扬州世界园艺博览会”约有3020000个相关结果,数据3020000用科学记数法表示为.10. 计算: .11. 在平面直角坐标系中,若点 在第二象限,则整数m的值为.12. 已知一组数据:a、4、5、6、7的平均数为5,则这组数据的中位数是.13. 扬州雕版印刷技艺历史悠久,元代数学家朱世杰的《算学启蒙》一书曾刻于扬州,该书是中国较早的数学著作之一,书中记载一道问题:“今有良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之?”题意是:快马每天走240里,慢马每天走150里,慢马先走12天,试问快马几天追上慢马?答:快马天追上慢马.14. 如图是某圆柱体果罐,它的主视图是边长为 的正方形,该果罐侧面积为 .
 15. 如图,在 中, ,点D是 的中点,过点D作 ,垂足为点E,连接 ,若 , ,则 .
15. 如图,在 中, ,点D是 的中点,过点D作 ,垂足为点E,连接 ,若 , ,则 .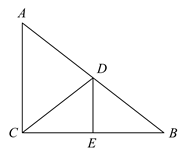 16. 如图,在 中,点E在 上,且 平分 ,若 , ,则 的面积为.
16. 如图,在 中,点E在 上,且 平分 ,若 , ,则 的面积为.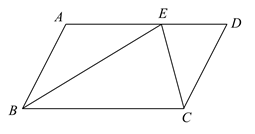 17. 如图,在 中, ,矩形 的顶点D、E在 上,点F、G分别在 、 上,若 , ,且 ,则 的长为.
17. 如图,在 中, ,矩形 的顶点D、E在 上,点F、G分别在 、 上,若 , ,且 ,则 的长为.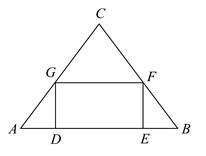 18. 将黑色圆点按如图所示的规律进行排列,图中黑色圆点的个数依次为:1,3,6,10,……,将其中所有能被3整除的数按从小到大的顺序重新排列成一组新数据,则新数据中的第33个数为.
18. 将黑色圆点按如图所示的规律进行排列,图中黑色圆点的个数依次为:1,3,6,10,……,将其中所有能被3整除的数按从小到大的顺序重新排列成一组新数据,则新数据中的第33个数为.
三、解答题
-
19. 计算或化简:(1)、 ;(2)、 .20. 已知方程组 的解也是关于x、y的方程 的一个解,求a的值.21. 为推进扬州市“青少年茁壮成长工程”,某校开展“每日健身操”活动,为了解学生对“每日健身操”活动的喜欢程度,随机抽取了部分学生进行调查,将调查信息结果绘制成如下尚不完整的统计图表:
抽样调查各类喜欢程度人数分布扇形统计图
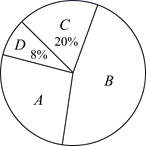
A.非常喜欢 B.比较喜欢 C.无所谓 D.不喜欢
抽样调查各类喜欢程度人数统计表
喜欢程度
人数
A.非常喜欢
50人
B.比较喜欢
m人
C.无所谓
n人
D.不喜欢
16人
根据以上信息,回答下列问题:
(1)、本次调查的样本容量是;(2)、扇形统计图中表示A程度的扇形圆心角为 ,统计表中 ;(3)、根据抽样调查的结果,请你估计该校2000名学生中大约有多少名学生喜欢“每日健身操”活动(包含非常喜欢和比较喜欢).22. 一张圆桌旁设有4个座位,丙先坐在了如图所示的座位上,甲、乙2人等可能地坐到①、②、③中的2个座位上. (1)、甲坐在①号座位的概率是;(2)、用画树状图或列表的方法,求甲与乙相邻而坐的概率.23. 为保障新冠病毒疫苗接种需求,某生物科技公司开启“加速”模式,生产效率比原先提高了20%,现在生产240万剂疫苗所用的时间比原先生产220万剂疫苗所用的时间少0.5天,问原先每天生产多少万剂疫苗?24. 如图,在 中, 的角平分线交 于点D, .
(1)、甲坐在①号座位的概率是;(2)、用画树状图或列表的方法,求甲与乙相邻而坐的概率.23. 为保障新冠病毒疫苗接种需求,某生物科技公司开启“加速”模式,生产效率比原先提高了20%,现在生产240万剂疫苗所用的时间比原先生产220万剂疫苗所用的时间少0.5天,问原先每天生产多少万剂疫苗?24. 如图,在 中, 的角平分线交 于点D, .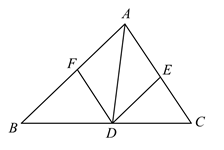 (1)、试判断四边形 的形状,并说明理由;(2)、若 ,且 ,求四边形 的面积.25. 如图,四边形 中, , , ,连接 ,以点B为圆心, 长为半径作 ,交 于点E.
(1)、试判断四边形 的形状,并说明理由;(2)、若 ,且 ,求四边形 的面积.25. 如图,四边形 中, , , ,连接 ,以点B为圆心, 长为半径作 ,交 于点E. (1)、试判断 与 的位置关系,并说明理由;(2)、若 , ,求图中阴影部分的面积.26. 如图,在平面直角坐标系中,二次函数 的图像与x轴交于点. 、 ,与y轴交于点C.
(1)、试判断 与 的位置关系,并说明理由;(2)、若 , ,求图中阴影部分的面积.26. 如图,在平面直角坐标系中,二次函数 的图像与x轴交于点. 、 ,与y轴交于点C.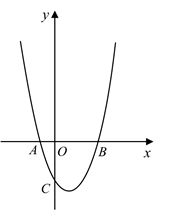 (1)、 , ;(2)、若点D在该二次函数的图象上,且 ,求点D的坐标;(3)、若点P是该二次函数图象上位于x轴上方的一点,且 ,直接写出点P的坐标.27. 在一次数学探究活动中,李老师设计了一份活动单:
(1)、 , ;(2)、若点D在该二次函数的图象上,且 ,求点D的坐标;(3)、若点P是该二次函数图象上位于x轴上方的一点,且 ,直接写出点P的坐标.27. 在一次数学探究活动中,李老师设计了一份活动单:已知线段 ,使用作图工具作 ,尝试操作后思考:
( 1 )这样的点A唯一吗?
( 2 )点A的位置有什么特征?你有什么感悟?
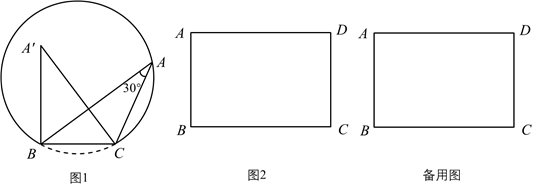
“追梦”学习小组通过操作、观察、讨论后汇报:点A的位置不唯一,它在以 为弦的圆弧上(点B、C除外),…….小华同学画出了符合要求的一条圆弧(如图1).
 (1)、小华同学提出了下列问题,请你帮助解决.
(1)、小华同学提出了下列问题,请你帮助解决.①该弧所在圆的半径长为;
② 面积的最大值为;
(2)、经过比对发现,小明同学所画的角的顶点不在小华所画的圆弧上,而在如图1所示的弓形内部,我们记为 ,请你利用图1证明 ;(3)、请你运用所学知识,结合以上活动经验,解决问题:如图2,已知矩形 的边长 , ,点P在直线 的左侧,且 .①线段 长的最小值为;
②若 ,则线段 长为.
28. 甲、乙两汽车出租公司均有50辆汽车对外出租,下面是两公司经理的一段对话:甲公司经理:如果我公司每辆汽车月租费3000元,那么50辆汽车可以全部租出.如果每辆汽车的月租费每增加50元,那么将少租出1辆汽车.另外,公司为每辆租出的汽车支付月维护费200元.
乙公司经理:我公司每辆汽车月租费3500元,无论是否租出汽车,公司均需一次性支付月维护费共计1850元.
说明:①汽车数量为整数;
②月利润=月租车费-月维护费;
③两公司月利润差=月利润较高公司的利润-月利润较低公司的利润.
在两公司租出的汽车数量相等的条件下,根据上述信息,解决下列问题:
(1)、当每个公司租出的汽车为10辆时,甲公司的月利润是元;当每个公司租出的汽车为辆时,两公司的月利润相等;(2)、求两公司月利润差的最大值;(3)、甲公司热心公益事业,每租出1辆汽车捐出a元 给慈善机构,如果捐款后甲公司剩余的月利润仍高于乙公司月利润,且当两公司租出的汽车均为17辆时,甲公司剩余的月利润与乙公司月利润之差最大,求a的取值范围.