初中数学苏科版九年级下册5.1 二次函数概念 同步练习
试卷更新日期:2021-06-22 类型:同步测试
一、单选题
-
1. 若函数 是关于x的二次函数,则m的值是( )A、2 B、-1或3 C、3 D、2. 下列函数中是二次函数的为( )A、y=3x-1 B、y=3x2-1 C、y=(x+1)2-x2 D、y=x3+2x-33. 下列 关于x的函数中,一定是二次函数的是( )A、 B、 C、 D、4. 在某种病毒的传播过程中,每轮传染平均1人会传染x个人,若最初2个人感染该病毒,经过两轮传染,共有y人感染.则y与x的函数关系式为( )A、 B、 C、 D、5. 若y=(m﹣1) 是关于x的二次函数,则m的值为( )A、﹣2 B、﹣2或1 C、1 D、不存在6. 若 是二次函数,且开口向上,则m的值为( )A、 B、 C、 D、07. 当函数 是二次函数时, 的取值为( )A、 B、 C、 D、8. 如果函数 是二次函数,则m的取值范围是( )A、 B、m=2 C、m=-2 D、m为全体实数9. 据省统计局公布的数据,安徽省2019年第二季度GDP总值约为7.9千亿元人民币,若我省第四季度GDP总值为y千亿元人民币,平均每个季度GDP增长的百分率为x , 则y关于x的函数表达式是( )A、y=7.9(1+2x) B、y=7.9(1-x)2 C、y=7.9(1+x)2 D、y=7.9+7.9(1+x)+7.9(1+x)210. 如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是(
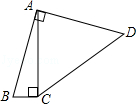 A、y= B、 y= C、 y= D、y=
A、y= B、 y= C、 y= D、y=二、填空题
-
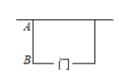
11. 已知函数y=(m﹣2) ﹣2是关于x的二次函数,则m= .12. 农机厂第一个月水泵的产量为50(台),第三个月的产量y(台)与月平均增长率x之间的关系表示为 .13. 若函数 是关于x的二次函数,则m的值为 .14. 用一根长为80cm的铁丝,把它弯成一个矩形,设矩形的面积为ycm2 , 一边长为xcm,则y与x的函数表达式为(化为一般式)15. 如图,用长为16m的篱笆,一面利用墙(墙足够长)围成一块留有一扇1m宽的门的长方形花圃.设花圃的宽AB为xm,面积为ym2 , 则y与x的函数表达式为 .
 16. 若函数 为关于 的二次函数,则 的值为.17. 如果二次函数 (m为常数)的图象有最高点,那么m的值为 .18. 矩形周长等于40,设矩形的一边长为 ,那么矩形面积 与边长 之间的函数关系式为.19. 若 是二次函数,则m=.20. 一台机器原价50万元,如果每年的折旧率是x,两年后这台机器的价格为y万元,则y与x的函数关系式为 .
16. 若函数 为关于 的二次函数,则 的值为.17. 如果二次函数 (m为常数)的图象有最高点,那么m的值为 .18. 矩形周长等于40,设矩形的一边长为 ,那么矩形面积 与边长 之间的函数关系式为.19. 若 是二次函数,则m=.20. 一台机器原价50万元,如果每年的折旧率是x,两年后这台机器的价格为y万元,则y与x的函数关系式为 .三、计算题
-
21. 一个二次函数y=(k﹣1) . 求k值.
四、解答题
-
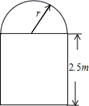
22. 当m为何值时,函数 是二次函数.23. 如果函数y=(m﹣3) +mx+1是二次函数,求m的值.24. 一条隧道的横截面如图所示,它的上部是一个半圆,下部是一个矩形,矩形的一边长为 米.如果隧道下部的宽度大于 米但不超过 米,求隧道横截面积 (平方米)关于上部半圆半径 (米)的函数解析式及函数的定义域.
 25. 已知y=(m-2) +3x+6是二次函数,求m的值,并判断此抛物线的开口方向,写出对称轴及顶点坐标.26. 已知函数y=(9k2﹣1)x2+2kx+3是关于x的二次函数,求不等式 的解集.27. 已知y=(m﹣1)x 是关于x的二次函数,求m的值.28. 若函数y=(a-1)x(b+1)+x2+1是二次函数,试讨论a、b的取值范围。
25. 已知y=(m-2) +3x+6是二次函数,求m的值,并判断此抛物线的开口方向,写出对称轴及顶点坐标.26. 已知函数y=(9k2﹣1)x2+2kx+3是关于x的二次函数,求不等式 的解集.27. 已知y=(m﹣1)x 是关于x的二次函数,求m的值.28. 若函数y=(a-1)x(b+1)+x2+1是二次函数,试讨论a、b的取值范围。
29. 已知函数 y=(m﹣1) +3x为二次函数,求m的值.30. 已知y=(m﹣2)x +3x+6是二次函数,求m的值.五、综合题
-
31. 小李家用 长的篱笆围成一个一边靠墙(墙足够长)的矩形菜园,如图.
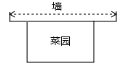 (1)、写出这块菜园的面积 与垂直于墙的边长 之间的函数解析式;
(1)、写出这块菜园的面积 与垂直于墙的边长 之间的函数解析式;
(2)、直接写出 的取值范围.
32. 已知函数y=(m﹣2)x2+mx﹣3(m为常数).(1)、当m时,该函数为二次函数;
(2)、当m时,该函数为一次函数.
33. 若y=(m﹣3) 是二次函数,
(1)、求m的值.
(2)、求出该图象上纵坐标为﹣6的点的坐标.
34. 根据下面的条件列出函数解析式,并判断列出的函数是否为二次函数:(1)、如果两个数中,一个比另一个大5,那么,这两个数的乘积p是较大的数m的函数;
(2)、一个半径为10cm的圆上,挖掉4个大小相同的正方形孔,剩余的面积S(cm2)是方孔边长x(cm)的函数;
(3)、有一块长为60m、宽为40m的矩形绿地,计划在它的四周相同的宽度内种植阔叶草,中间种郁金香,那么郁金香的种植面积S(cm2)是草坪宽度a(m)的函数.
35. 已知函数y=(m2-m)x2+(m-1)x+2-2m.
(1)、若这个函数是二次函数,求m的取值范围.(2)、若这个函数是一次函数,求m的值.(3)、这个函数可能是正比例函数吗?为什么?
36. 李明准备进行如下操作实验,把一根长40 cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.(1)、要使这两个正方形的面积之和等于58 cm2 , 李明应该怎么剪这根铁丝?(2)、李明认为这两个正方形的面积之和不可能等于48 cm2 , 你认为他的说法正确吗?请说明理由.37. 某公司销售一种新型节能电子小产品,现准备从国内和国外两种销售方案中选择一种进行销售:①若只在国内销售,销售价格y(元/件)与月销量x(件)的函数关系式为y=﹣ x+150,成本为20元/件,月利润为W内(元);②若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳 x2元的附加费,月利润为W外(元).(1)、若只在国内销售,当x=1000(件)时,y=(元/件);(2)、分别求出W内、W外与x间的函数关系式(不必写x的取值范围);(3)、若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求a的值.38. 某商场购进一种单价为40元的商品,如果以单价60元售出,那么每天可卖出300个,根据销售经验,每降价1元,每天可多卖出20个,假设每个降价x(元),每天销售y(个),每天获得利润W(元).(1)、写出y与x的函数关系式;(2)、求出W与x的函数关系式(不必写出x的取值范围)39. 一经销商按市场价收购某种海鲜1000斤放养在池塘内(假设放养期内每个海鲜的重量基本保持不变),当天市场价为每斤30元,据市场行情推测,此后该海鲜的市场价每天每斤可上涨1元,但是平均每天有10斤海鲜死去.假设死去的海鲜均于当天以每斤20元的价格全部售出.(1)、用含x的代数式填空:①x天后每斤海鲜的市场价为元;
②x天后死去的海鲜共有斤;死去的海鲜的销售总额为元;
③x天后活着的海鲜还有斤;
(2)、如果放养x天后将活着的海鲜一次性出售,加上已经售出的死去的海鲜,销售总额为y1 , 写出y1关于x的函数关系式;(3)、若每放养一天需支出各种费用400元,写出经销商此次经销活动获得的总利润y2关于放养天数x的函数关系式.40. 已知两个变量x,y之间的关系式为y=(a﹣2)x2+(b+2)x﹣3.(1)、当时,x,y之间是二次函数关系;(2)、当时,x,y之间是一次函数关系.
-