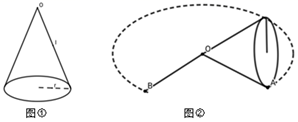
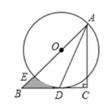
初中数学苏科版九年级上册2.7-2.8 弧长、扇形及圆锥同步练习

试卷更新日期：2021-06-22 类型：同步测试

进入出卷网下载

一、单选题

1. 如图，从一张腰长为 $90 cm$ ，顶角为 $120 °$ 的等腰三角形铁皮 $O A B$ 中剪出一个最大的扇形 $O C D$ ，用此剪下的扇形铁皮围成一个圆锥的侧面（不计损耗），则该圆锥的底面周长为（）

A、 $60 π cm$ B、 $50 π cm$ C、 $40 π cm$ D、 $30 π cm$

查看试题解析
2. 如图，在Rt△ABC中，∠A＝90°，BC＝ $4 \sqrt{2}$ ．以BC的中点O为圆心的⊙O分别与AB ， AC相切于D ， E两点，则 $\overset{⌢}{D E}$ 的长为（　　）

A、 $\frac{π}{2}$ B、π C、2π D、4π

查看试题解析
3. 如图，正六边形ABCDEF内接于⊙O ，边长AB＝2，则扇形AOB的面积为（　　）

A、 $\frac{π}{3}$ B、 $\frac{2 π}{3}$ C、π D、 $\frac{4 π}{3}$

查看试题解析
4. 如图，一块直角三角板的60°角的顶点A落在⊙O上，两边分别交⊙O于B，C两点，若⊙O的半径是1，则 $\overset{⌢}{B C}$ 的长是（）

A、 $\frac{π}{3}$ B、 $\frac{π}{2}$ C、 $\frac{2 π}{3}$ D、 $\frac{5 π}{6}$

查看试题解析
5. 某扇形的圆心角为 $150 °$ ，其弧长为 $20 π cm$ ，则此扇形的面积是（）

A、 $120 π cm$ B、 $480 π {cm}^{2}$ C、 $240 π {cm}^{2}$ D、 $240 {cm}^{2}$

查看试题解析
6. 如图，已知圆锥侧面展开图的扇形面积为65 $π$ cm2，扇形的弧长为10 $π$ cm，则圆锥母线长是（）

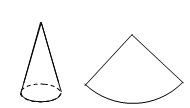A、5cm B、10cm C、12cm D、13cm

查看试题解析
7. 如图，在纸上剪一个圆形和一个扇形的纸片，使之恰好能围成一个圆锥模型，若圆的半径r＝1，扇形的半径为R，扇形的圆心角等于90°，则R的值是（）

A、R＝2 B、R＝3 C、R＝4 D、R＝5

查看试题解析
8. 如图所示，矩形纸片ABCD中，AB＝4cm，把它分割成正方形纸片ABFE和矩形纸片EFCD后，分别裁出扇形ABF和半径最大的圆，恰好能作为一个圆锥的侧面和底面，则底面圆的直径的长为（）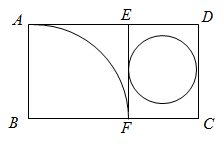

A、2cm B、3cm C、4cm D、5cm

查看试题解析
9. 有一条弧的长为2πcm ，半径为2cm ，则这条弧所对的圆心角的度数是（）

A、90° B、120° C、180° D、135°

查看试题解析
10. 已知一个圆锥的侧面展开图是一个半圆，则该圆锥的母线与底面半径所成角的度数是（）

A、 $15 °$ B、 $30 °$ C、 $45 °$ D、 $60 °$

查看试题解析

二、填空题

11. 在一个圆中60度的圆心角所对的弧长为 $\frac{2}{3} π$ ，则该圆的直径为

查看试题解析
12. 在半径为12的圆中， $60 °$ 圆心角所对的弧长是.

查看试题解析
13. 如图，⊙O是△ABC的外接圆，半径是2，∠BAC＝60°，则 $\overset{⌢}{B C}$ 的长是．

查看试题解析
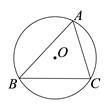14. 一个圆锥的底面半径r=6，母线l=10，则这个圆锥的侧面积是

查看试题解析
15. 用半径为12cm，圆心角为60°的扇形纸片围成一个圆锥的侧面(接缝忽略不计)，则该圆锥底面圆的半径为cm

查看试题解析
16. 圆锥的底面圆的半径是3，其母线长是9，则圆锥侧面展开图的扇形的圆心角度数是.

查看试题解析
17. 已知扇形的圆心角为60°，弧长为2πcm，则扇形的面积为cm² ．（计算结果保留π）

查看试题解析
18. 将半径为12，圆心角为 $120 °$ 的扇形围成一个圆锥侧面，则此圆锥的高为．

查看试题解析
19. 如图，用圆心角为 $120 °$ 半径为6的扇形围成一个圆锥的侧面（接缝忽略不计），则这个圆锥的高是.

查看试题解析
20. 如图将⊙O沿弦AB折叠， $\overset{⌢}{A B}$ 恰好经过圆心O，若⊙O的半径为3，则 $\overset{⌢}{A B}$ 的长为．

查看试题解析

三、解答题

21. 一个圆锥的母线长为 $10,$ 底面半径为 $5$ ，求这个圆锥的侧面积和全面积.

查看试题解析
22. 已知半径为6的扇形面积为 $12 π$ ，求此扇形圆心角的角度.

查看试题解析
23. 如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形，若圆锥的底面圆的半径 $r = 2 cm$ ，扇形的圆心角 $θ = 120 °$ ，求该圆锥的母线长 $l$ ．

查看试题解析
24. 如图，将弧长为 $6 π$ ，圆心角为120°的扇形纸片 $A O B$ 围成圆锥形纸帽，使扇形的两条半径 $O A$ 与 $O B$ 重合（接缝粘连部分忽略不计），求圆锥的底面圆半径及圆锥的侧面积．

查看试题解析
25. 如图所示，在 Rt△ABC中，∠C=90°，AC=4 ，BC=3 .求以直角边所在直线为轴，把△ABC 旋转一周得到的圆锥的侧面积.

查看试题解析
26. 如图①是山东舰徽的构图，采用航母 $45$ 度破浪而出的角度，展现山东舰作为中国首艘国产舰母横空出世的气势，将舰徽中第一条波浪抽象成几何图形，则是一条长为 $10 π$ 的弧，若该弧所在的扇形是高为 $12$ 的圆锥侧面展开图(如图②)，则该圆锥的母线长 $A B$ 为多少?

查看试题解析
27. 如图，⊙A、⊙B、⊙C两两不相交，且半径都是2cm，图中的三个扇形（即三个阴影部分）的面积之和是多少？弧长的和为多少?

查看试题解析
28. 如图， $A B C D$ 为正方形， $A B = 4$ ，以点 $A$ 为圆心， $A B$ 为半径画弧得到扇形 $A B D$ ，现将该扇形围成一圆锥的侧面，求该圆锥底面圆的半径.

查看试题解析
29. 如图从一块半径为 $1 m$ 的圆形铁皮上剪出一个圆心角为 $90^{\circ}$ 的扇形，再把此扇形围成一个圆锥，求圆锥的底面半径.

查看试题解析
30. 小明同学用纸板制作了一个圆锥形漏斗模型，如图所示，它的底面半径 $O B = 3 c m$ ，高 $O C = 4 c m$ ，求这个圆锥形漏斗的侧面积．

查看试题解析
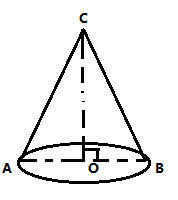31. 如图是一纸杯，它的母线AC和EF延长后形成的立体图形是圆锥，该圆锥的侧面展开图形是扇形OAB．经测量，纸杯上开口圆的直径是6cm，下底面直径为4cm，母线长为EF=8cm．求扇形OAB的圆心角及这个纸杯的表面积（面积计算结果用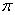表示）．

查看试题解析
32. 如图，AE是半圆O的直径，弦AB=BC=2 $\sqrt{2}$ ，弦CD=DE=2，连结OB，OD，求图中两个阴影部分的面积和．

查看试题解析
33.
如图，在Rt△ABC中，∠C=90°，∠BAC=30°，BC=1，以B为圆心，BA为半径画弧交CB的延长线于点D，求弧AD的长

查看试题解析

四、作图题

34. 一个等腰Rt△ABC如图所示，将它绕着直线AC旋转一周，形成一个几何体.

(1)、画出这个几何体的三视图.

(2)、依据图中的测量数据，计算这个几何体的表面积.

查看试题解析

五、综合题

35. 如图，已知圆柱底面的直径 $B C = 8$ ，圆柱的高 $A B = 10$ ，在圆柱的侧面上，过点 $A$ ， $C$ 嵌有一圈长度最短的金属丝.

(1)、现将圆柱侧面沿 $A B$ 剪开，所得的圆柱侧面展开图是______.

A、； B、； C、； D、

(2)、求该长度最短的金属丝的长.

查看试题解析
36. 某灯具厂生产一批台灯罩，如图的阴影部分为灯罩的侧面展开图.已知半径 $O A = 24 cm$ ， $O C = 12 cm$ ， $∠ A O B = 135 °$ .（计算结果保留 $π$ ）

(1)、若要在灯罩的上下边缘镶上花边（花边的宽度忽略不计），至少需要多长的花边？

(2)、求灯罩的侧面积（接缝处忽略不计）.

查看试题解析
37. 已知，如图，扇形AOB的圆心角为120°，半径OA为6cm.

(1)、求扇形AOB的弧长和扇形面积；

(2)、若把扇形纸片AOB卷成一个圆锥无底纸盒，求这个纸盒的高OH.

查看试题解析
38. 如图①，已知圆锥的母线长l=16cm，若以顶点O为中心，将此圆锥按图②放置在平面上逆时针滚动3圈后所形成的扇形的圆心角θ=270°.

(1)、求圆锥的底面半径；

(2)、求圆锥的表面积.

查看试题解析
39. 如图，在Rt△ABC中，∠C=90°，AC=BC，点O在AB上，以O为圆心，OA为半径作⊙O，与BC相切于点D，且交AB于点E。

(1)、连结AD，求证：AD平分∠CAB；

(2)、若BE= $\sqrt{2}$ -1，求阴影部分的面积。

查看试题解析
40. 一个圆锥的高为3 $\sqrt{3}$ cm，侧面展开图是半圆，求：

(1)、圆锥母线长与底面半径的比；

(2)、圆锥的全面积．

查看试题解析

初中数学苏科版九年级上册2.7-2.8 弧长、扇形及圆锥 同步练习

一、单选题

二、填空题

三、解答题

四、作图题

五、综合题

初中数学苏科版九年级上册2.7-2.8 弧长、扇形及圆锥同步练习