初中数学苏科版九年级上册2.6正多边形与圆同步练习

试卷更新日期：2021-06-22 类型：同步测试

进入出卷网下载

一、单选题

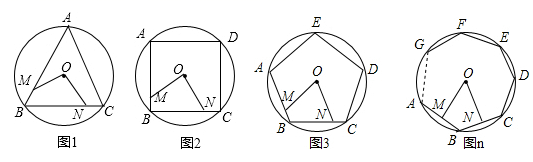
1. 在正六边形ABCDEF的中，若BE=10，则这个正六边形外接圆半径是（）

A、 $\frac{5}{2}$ B、5 C、 $\frac{5}{2} \sqrt{3}$ D、5 $\sqrt{3}$

查看试题解析
2. 已知正六角形的边心距为 $\sqrt{3}$ ，则它的周长是（）

A、6 B、12 C、6 $\sqrt{3}$ D、12 $\sqrt{3}$

查看试题解析
3. 已知圆内接正六边形的半径为2，则该内接正六边形的边心距为（）

A、2 B、1 C、 $\sqrt{3}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
4. 如图，五边形 $A B C D E$ 是 $⊙ O$ 的内接正五边形， $A F$ 是 $⊙ O$ 的直径，则 $∠ B D F$ 的度数是（）

A、18° B、36° C、 $54 °$ D、72°

查看试题解析
5. 如图，正六边形ABCDEF内接于于⊙O，连接BD，则∠CBD的度数是（）

A、30° B、45° C、60° D、90°

查看试题解析
6. 如图，四边形ABCD为⊙O的内接正四边形，△AEF为⊙O的内接正三角形，若DF恰好是同圆的一个内接正n边形的一边，则n的值为（）

A、8 B、10 C、12 D、15

查看试题解析
7. 若⊙O的内接正n边形的边长与⊙O的半径相等，则n的值为（）

A、4 B、5 C、6 D、7

查看试题解析
8. 正多边形的内切圆与外接圆的半径之比为 $\frac{\sqrt{2}}{2}$ ，则这个正多边形为（）

A、正十二边形 B、正六边形 C、正四边形 D、正三角形

查看试题解析
9. 一个圆的内接正六边形与内接正方形的边长之比为（）

A、3：2 B、 $1 ： \sqrt{3}$ C、 $1 ： \sqrt{2}$ D、 $\sqrt{2} ： \sqrt{3}$

查看试题解析
10. 正方形外接圆的半径为4，则其内切圆的半径为（）

A、2 $\sqrt{2}$ B、 $\sqrt{2}$ C、1 D、 $\frac{\sqrt{2}}{2}$

查看试题解析
11. 已知正六边形 $A B C D E F$ 内接于 $⊙ O$ ，若 $⊙ O$ 的直径为 $2$ ，则该正六边形的周长是（）

A、 $12$ B、 $6 \sqrt{3}$ C、 $6$ D、 $3 \sqrt{3}$

查看试题解析
12. 已知⊙O的半径是2，一个正方形内接于⊙O，则这个正方形的边长是（）

A、2 $\sqrt{2}$ B、2 C、 $\sqrt{2}$ D、4

查看试题解析
13. 半径为 $a$ 的圆的内接正六边形的边心距是（）

A、 $\frac{a}{2}$ B、 $\frac{\sqrt{2} a}{2}$ C、 $\frac{\sqrt{3} a}{2}$ D、 $a$

查看试题解析
14. 边长为6的正三角形的外接圆的周长为（）

A、 $\sqrt{3} π$ B、 $2 \sqrt{3} π$ C、 $3 \sqrt{3} π$ D、 $4 \sqrt{3} π$

查看试题解析
15. 半径为 $R$ 的圆内接正三角形的面积是（）

A、 $\frac{\sqrt{3}}{2} R^{2}$ B、 $π R^{2}$ C、 $\frac{3 \sqrt{3}}{2} R^{2}$ D、 $\frac{3 \sqrt{3}}{4} R^{2}$

查看试题解析
16. 如图，在圆内接正六边形ABCDEF中，BF，BD分别交AC于点G，H.若该圆的半径为15cm，则线段GH的长为（）

A、 $\sqrt{5}$ cm B、5 $\sqrt{3}$ cm C、3 $\sqrt{5}$ cm D、10 $\sqrt{3}$ cm

查看试题解析
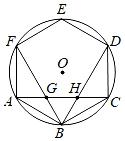17. 以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则（）

A、不能构成三角形 B、这个三角形是等腰三角形 C、这个三角形是直角三角形 D、这个三角形是钝角三角形

查看试题解析

二、填空题

18. 如图，A、B、C、D为一个正多边形的相邻四个顶点，O为正多边形的中心，若∠ADB=12°，则这个正多边形的边数为

查看试题解析
19. 如图，正五边形 $A B C D E$ 内接于 $⊙ O$ ，点 $F$ 在弧 $C D$ 上，则 $∠ B F E$ 的度数为

查看试题解析
20. 若圆内接正方形的边心距为3，则这个圆内接正三角形的边长为.

查看试题解析
21. 数学家刘徽首创割圆术，用圆内接正多边形的面积去无限逼近圆面积并以此求出圆周率.如图，正六边形 $A B C D E F$ 的边长为2，现随机向该图形内掷一枚小针，则针尖落在阴影区域的概率为.

查看试题解析
22. 如图，正五边形 $A B C D E$ 内接于 $⊙ O$ ，F是 $\overset{⌢}{C D}$ 的中点，则 $∠ C B F$ 的度数为.

查看试题解析
23. 边长等于 $4 cm$ 的正六边形的外接圆半径等于 $cm$ .

查看试题解析
24. 如图，正六边形ABCDEF内接于 $⊙ O$ ，若 $A B = 3 cm$ ，则 $⊙ O$ 的半径为.

查看试题解析
25. 我国古代数学家刘徽创造的“割圆术”，利用了圆内接正多边形和外切正多边形的面积或周长，无限逼近圆来近似估计圆的面积或周长，从而估算出π的范围.如图1，用圆内接正方形和外切正方形周长可得2 $\sqrt{2}$ <r<4，那么利用图2中的圆内接正六边形和外切正六边形周长可进一步将π的范围缩小到(结果保留根号)

查看试题解析
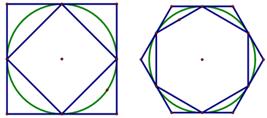26. 正六边形的半径为 $1 ，$ 则正六边形的面积为.

查看试题解析
27. 2020年3月14日是全球首个国际圆周率日（π Day）．历史上求圆周率π的方法有多种，与中国传统数学中的“割圆术”相似．数学家阿尔 $\cdot$ 卡西的计算方法是：当正整数n充分大时，计算某个圆的内接正6n边形的周长和外切正6n边形 $($ 各边均与圆相切的正6n边形 $)$ 的周长，再将它们的平均数作为2π的近似值．当n=1时，右图是⊙O及它的内接正六边形和外切正六边形．

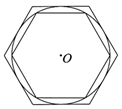(1)、若⊙O的半径为1，则⊙O的内接正六边形的边长是；

(2)、按照阿尔 $\cdot$ 卡西的方法，计算n=1时π的近似值是．（结果保留两位小数）（参考数据： $\sqrt{3} \approx 1.732$ ）

查看试题解析
28. 如图，正 $△ A B C$ 内接于半径为1cm的圆，则阴影部分的面积为。

查看试题解析
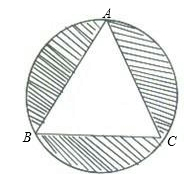29. 如图，在平面直角坐标系中，正六边形 $O A B C D E$ 的边长是2，则它的外接圆圆心 $P$ 的坐标是．

查看试题解析
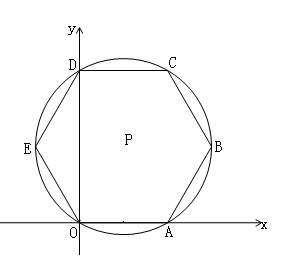30. 一个半径为4cm的圆内接正六边形的面积等于cm² ．

查看试题解析
31. 如图，正六边形ABCDEF内接于 $⊙ O$ ，半径为4，则这个正六边形的边心距OM的长为．

查看试题解析
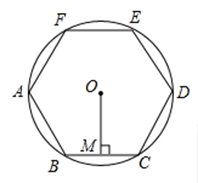32. 边长为2的正方形ABCD的外接圆半径是．

查看试题解析

三、解答题

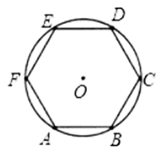
33. 如图，已知圆O内接正六边形 $A B C D E F$ 的边长为 $6 cm$ ，求这个正六边形的边心距n ，面积S ．

查看试题解析

四、综合题

34. 圆周率 $π$ 的故事
我国古代数学家刘徽通过“割圆术”来估计圆周率 $π$ 的值——“割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体，而无所失矣”，可以理解为当正多边形的边数越来越多时，该正多边形与它的外接圆越来越“接近”，这样就可以用正多边形的周长替代它的外接圆的周长，从而估算出圆周率 $π$ 的值.

(1)、对于边长为a的正方形，其外接圆半径为，根据故事中的方法，用该正方形的周长4a替代它的外接圆周长，利用公式 $C = 2 π r$ ，可以估算 $π = \frac{C}{2 r} =$ .

(2)、类比（1），当正多边形为正六边形时，估计 $π$ 的值.

查看试题解析
35. 如图，正方形ABCD内接于⊙O，E是 $\overset{⌢}{B C}$ 的中点，连接AE，DE，CE.

(1)、求证：AE=DE；

(2)、若CE=1，求四边形AECD的面积.

查看试题解析
36. 如图M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDEFG…的边AB、BC上的点，且BM＝CN，连接OM、ON

(1)、求图1中∠MON的度数

(2)、图2中∠MON的度数是，图3中∠MON的度数是

(3)、试探究∠MON的度数与正n边形边数n的关系是

查看试题解析

初中数学苏科版九年级上册2.6正多边形与圆 同步练习

一、单选题

二、填空题

三、解答题

四、综合题

初中数学苏科版九年级上册2.6正多边形与圆同步练习