初中数学苏科版九年级上册2.1-2.5 同步测试卷
试卷更新日期:2021-06-22 类型:单元试卷
一、单选题
-
1. 如图,点 , , 在 上, , ,则 的度数为( )
 A、 B、 C、 D、2. 如图,在正八边形ABCDEFGH中,连接AC,AE,则的值是( )
A、 B、 C、 D、2. 如图,在正八边形ABCDEFGH中,连接AC,AE,则的值是( ) A、1 B、 C、2 D、3. 如图,△ABC内接于⊙O,∠OBC=40°,则∠A的度数为( )
A、1 B、 C、2 D、3. 如图,△ABC内接于⊙O,∠OBC=40°,则∠A的度数为( ) A、80° B、100° C、110° D、130°4. 如图, 的圆心 的坐标为 ,半径为1,直线 的表达式为 , 是直线 上的动点, 是 上的动点,则 的最小值是( )
A、80° B、100° C、110° D、130°4. 如图, 的圆心 的坐标为 ,半径为1,直线 的表达式为 , 是直线 上的动点, 是 上的动点,则 的最小值是( )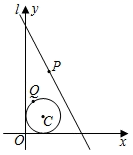 A、 B、 C、 D、5.
A、 B、 C、 D、5.如图,在⊙O中,∠ABC=130°,则∠AOC等于( )
 A、50° B、80° C、90° D、100°6. 如图是某个球放进盒子内的截面图,球的一部分露出盒子外,已知⊙O交矩形ABCD的边AD于点E,F,已知AB=EF=2,则球的半径长为( )
A、50° B、80° C、90° D、100°6. 如图是某个球放进盒子内的截面图,球的一部分露出盒子外,已知⊙O交矩形ABCD的边AD于点E,F,已知AB=EF=2,则球的半径长为( ) A、 B、 C、 D、7. 在Rt△ABC中,∠ACB = 90°,AC = 9,BC = 12,则其外接圆的半径为( )
A、 B、 C、 D、7. 在Rt△ABC中,∠ACB = 90°,AC = 9,BC = 12,则其外接圆的半径为( ) A、15 B、7.5 C、6 D、38. 如图,点A,B,C在 上,且 ,则 的度数是( )
A、15 B、7.5 C、6 D、38. 如图,点A,B,C在 上,且 ,则 的度数是( )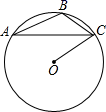 A、 B、 C、 D、9. 已知点O是 的外心,作正方形 ,下列说法:①点O是 的外心;②点O是 的外心;③点O是 的外心;④点O是 的外心.其中说法一定正确的是( )A、②④ B、①③ C、②③④ D、①③④10. 如图,圆 为 的外接圆, ,则 的度数为( )
A、 B、 C、 D、9. 已知点O是 的外心,作正方形 ,下列说法:①点O是 的外心;②点O是 的外心;③点O是 的外心;④点O是 的外心.其中说法一定正确的是( )A、②④ B、①③ C、②③④ D、①③④10. 如图,圆 为 的外接圆, ,则 的度数为( ) A、15° B、18° C、28° D、30°11. 已知四边形ABCD,下列命题:①若 ,则四边形ABCD一定存在外接圆;②若四边形ABCD内存在一点到四个顶点的距离相等,则 ;③若四边形ABCD内存在一点到四条边的距离相等,则 ,其中,真命题的个数为( )A、0 B、1 C、2 D、312. 如图,AB是⊙O的直径,BC是⊙O的切线.点D、E在⊙O上,若∠CBD=110°,则∠E的度数是( )
A、15° B、18° C、28° D、30°11. 已知四边形ABCD,下列命题:①若 ,则四边形ABCD一定存在外接圆;②若四边形ABCD内存在一点到四个顶点的距离相等,则 ;③若四边形ABCD内存在一点到四条边的距离相等,则 ,其中,真命题的个数为( )A、0 B、1 C、2 D、312. 如图,AB是⊙O的直径,BC是⊙O的切线.点D、E在⊙O上,若∠CBD=110°,则∠E的度数是( ) A、90° B、80° C、70° D、60°
A、90° B、80° C、70° D、60°二、填空题
-
13. 在平面直角坐标系中,直线y=﹣x+6分别与x轴、y轴交于点A、B两点,点C在y轴左边,且∠ACB=90°,则点C的横坐标xc的取值范围是.14. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC.若∠CAB=22.5°,CD=8cm,则⊙O的半径为 cm.
 15. 如图,在 中, , , ,P是 所在平面内一点,且满足 ,则 的最大值为.
15. 如图,在 中, , , ,P是 所在平面内一点,且满足 ,则 的最大值为.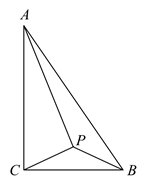 16. 已知 的半径为 , ,则点P在 的.(填“上面”“内部”或“外部”)17. 如图,在⊙O的内接四边形ABCD中,∠A=70°,∠OBC=60°,则∠ODC= .
16. 已知 的半径为 , ,则点P在 的.(填“上面”“内部”或“外部”)17. 如图,在⊙O的内接四边形ABCD中,∠A=70°,∠OBC=60°,则∠ODC= . 18. 如图,已知点 在 轴正半轴上,圆 与 轴相切于原点 ,平行于 轴的直线交圆 于 两点,点 在点 的下方,且点 的坐标是 ,则圆 的半径为.
18. 如图,已知点 在 轴正半轴上,圆 与 轴相切于原点 ,平行于 轴的直线交圆 于 两点,点 在点 的下方,且点 的坐标是 ,则圆 的半径为. 19. 如图,在圆内接四边形ABCD中, 、 、 的度数之比为 ,则 .
19. 如图,在圆内接四边形ABCD中, 、 、 的度数之比为 ,则 . 20. 如图,在平面直角坐标系中,一个圆经过 , , 三点,则该圆的圆心的坐标是.
20. 如图,在平面直角坐标系中,一个圆经过 , , 三点,则该圆的圆心的坐标是. 21. 如图,正五边形ABCDE内接于⊙O,连接BD,则∠ABD=°.
21. 如图,正五边形ABCDE内接于⊙O,连接BD,则∠ABD=°. 22. 如图, 是 的直径,点C、D是 两侧 上的点,若 ,则 .
22. 如图, 是 的直径,点C、D是 两侧 上的点,若 ,则 .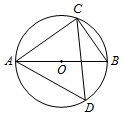 23. 如图,四边形ABCD内接于⊙O,AB是直径, , ,则 的度数为.
23. 如图,四边形ABCD内接于⊙O,AB是直径, , ,则 的度数为. 24. 在 ABC中,∠BAC=100°,AB=AC,D为 ABC形外一点,且AD=AC,则∠BDC=°.25. 如图,C、D是半圆O上两点,AB是直径,若AD=CD=2,CB=4,则半圆的半径为.
24. 在 ABC中,∠BAC=100°,AB=AC,D为 ABC形外一点,且AD=AC,则∠BDC=°.25. 如图,C、D是半圆O上两点,AB是直径,若AD=CD=2,CB=4,则半圆的半径为. 26. 如图,已知⊙O为△ABC的内切圆,D、E、F为切点,P是⊙O上异于E、F的一动点,若∠ A+∠C=x°,∠EPF=y°,则y与x的函数关系式为 .
26. 如图,已知⊙O为△ABC的内切圆,D、E、F为切点,P是⊙O上异于E、F的一动点,若∠ A+∠C=x°,∠EPF=y°,则y与x的函数关系式为 .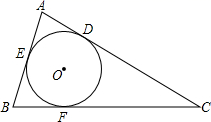
三、综合题
-
27. 如图,已知 的直径 ,弦 ,D是 的中点,过点D作 ,交 的延长线于点E.
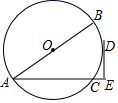 (1)、求证: 是 的切线;(2)、求 的长.28. 如图,AB=AC=6,∠BAC为锐角,CD∥AB.
(1)、求证: 是 的切线;(2)、求 的长.28. 如图,AB=AC=6,∠BAC为锐角,CD∥AB.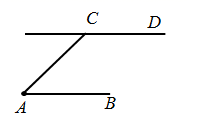 (1)、在直线CD上求作点P,使∠ABP= ∠BAC.写出作法,并说明作图理由;(2)、若∠BAC=45°,求线段PC的长.29. 如图,AB是⊙O的直径,C为⊙O上一点,M是半径OB上动点(不与O、B重合),过点M作EM⊥AB,交BC于点D,交AC的延长线于点E,点F为ED的中点,连接FC.
(1)、在直线CD上求作点P,使∠ABP= ∠BAC.写出作法,并说明作图理由;(2)、若∠BAC=45°,求线段PC的长.29. 如图,AB是⊙O的直径,C为⊙O上一点,M是半径OB上动点(不与O、B重合),过点M作EM⊥AB,交BC于点D,交AC的延长线于点E,点F为ED的中点,连接FC. (1)、求证:FC为⊙O的切线;(2)、当M为OB的中点时,若CE=8,CF=5,求⊙O的半径长.30. 如图, 是 的切线,A为切点,点B、C、D在 上,且 .
(1)、求证:FC为⊙O的切线;(2)、当M为OB的中点时,若CE=8,CF=5,求⊙O的半径长.30. 如图, 是 的切线,A为切点,点B、C、D在 上,且 .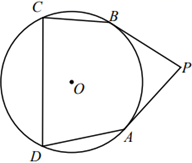 (1)、求证: 是 的切线;(2)、若 ,则 的度数为°.31. 如图,在 中,E是AD上一点,延长CE到点F,使得 .
(1)、求证: 是 的切线;(2)、若 ,则 的度数为°.31. 如图,在 中,E是AD上一点,延长CE到点F,使得 . (1)、求证: ;(2)、请用无刻度直尺与圆规在AD上求作一点P,使 .(保留作图痕迹,不写作法)32. 如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形,建立如图所示的平面直角坐标系,点C的坐标为(0,﹣1).
(1)、求证: ;(2)、请用无刻度直尺与圆规在AD上求作一点P,使 .(保留作图痕迹,不写作法)32. 如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形,建立如图所示的平面直角坐标系,点C的坐标为(0,﹣1). (1)、在如图的方格纸中把△ABC以点O为位似中心扩大,使放大前后的位似比为1:2,画出△A1B1C1(△ABC与△A1B1C1在位似中心O点的两侧,A,B,C的对应点分别是A1 , B1 , C1).(2)、利用方格纸标出△A1B1C1外接圆的圆心P,P点坐标是 , ⊙P的半径=.(保留根号)33. 如图,已知 是 的直径,点 、 在 上,点 在 外, .
(1)、在如图的方格纸中把△ABC以点O为位似中心扩大,使放大前后的位似比为1:2,画出△A1B1C1(△ABC与△A1B1C1在位似中心O点的两侧,A,B,C的对应点分别是A1 , B1 , C1).(2)、利用方格纸标出△A1B1C1外接圆的圆心P,P点坐标是 , ⊙P的半径=.(保留根号)33. 如图,已知 是 的直径,点 、 在 上,点 在 外, .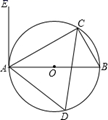 (1)、 度;(2)、求证: 是 的切线;(3)、当 时,求劣弧 的长.
(1)、 度;(2)、求证: 是 的切线;(3)、当 时,求劣弧 的长.