初中数学苏科版九年级上册2.5 直线与圆位置关系 同步练习
试卷更新日期:2021-06-22 类型:同步测试
一、单选题
-
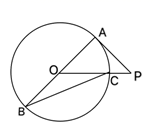
1. 如图,AB是⊙O的直径,PA切⊙O于点A,线段PO交⊙O于点C,连结BC,若∠P=40°,则∠B等于( )
 A、15° B、20° C、25° D、30°2. 已知⊙O的直径为4,点O到直线m的距离为2,则直线m与⊙O的位置关系是( )A、相交 B、相切 C、相离 D、无法判断3. 已知 的半径是 ,圆心 到同一平面内直线 的距离为 ,则直线 与 的位置关系是( )A、相交 B、相切 C、相离 D、无法判断4. ⊙O的半径为7,圆心O到直线l的距离为6,则直线l与⊙O的位置关系是( )A、相交 B、相切 C、相离 D、无法确定5. 已知⊙O的直径为12cm,如果圆心O到一条直线的距离为7cm,那么这条直线与这个圆的位置关系是( )A、相离 B、相切 C、相交 D、相交或相切6. 已知⊙O的半径为5,圆心O到直线AB的距离为6,则直线AB于⊙O的位置关系是( )A、相交 B、相切 C、相离 D、无法确定7. 已知⊙O的半径为5,直线l与⊙O相交,点O到直线l的距离为3,则⊙O上到直线l的距离为2的点共有( )A、1个 B、2个 C、3个 D、4个8. 如图,在 中,AB是直径,AC是弦,过点C的切线与AB的延长线交于点D,若 ,则 的大小为
A、15° B、20° C、25° D、30°2. 已知⊙O的直径为4,点O到直线m的距离为2,则直线m与⊙O的位置关系是( )A、相交 B、相切 C、相离 D、无法判断3. 已知 的半径是 ,圆心 到同一平面内直线 的距离为 ,则直线 与 的位置关系是( )A、相交 B、相切 C、相离 D、无法判断4. ⊙O的半径为7,圆心O到直线l的距离为6,则直线l与⊙O的位置关系是( )A、相交 B、相切 C、相离 D、无法确定5. 已知⊙O的直径为12cm,如果圆心O到一条直线的距离为7cm,那么这条直线与这个圆的位置关系是( )A、相离 B、相切 C、相交 D、相交或相切6. 已知⊙O的半径为5,圆心O到直线AB的距离为6,则直线AB于⊙O的位置关系是( )A、相交 B、相切 C、相离 D、无法确定7. 已知⊙O的半径为5,直线l与⊙O相交,点O到直线l的距离为3,则⊙O上到直线l的距离为2的点共有( )A、1个 B、2个 C、3个 D、4个8. 如图,在 中,AB是直径,AC是弦,过点C的切线与AB的延长线交于点D,若 ,则 的大小为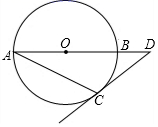 A、 B、 C、 D、9. 已知同一平面内有⊙O和点A与点B , 如果O的半径为3cm,线段OA=5cm,线段OB=3cm,那么直线AB与⊙O的位置关系为( )A、相离 B、相交 C、相切 D、相交或相切10. 如图,点B在⊙A上,点C在⊙A外,以下条件不能判定BC是⊙A切线的是( )
A、 B、 C、 D、9. 已知同一平面内有⊙O和点A与点B , 如果O的半径为3cm,线段OA=5cm,线段OB=3cm,那么直线AB与⊙O的位置关系为( )A、相离 B、相交 C、相切 D、相交或相切10. 如图,点B在⊙A上,点C在⊙A外,以下条件不能判定BC是⊙A切线的是( )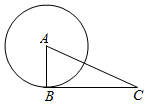 A、∠A=50°,∠C=40° B、∠B﹣∠C=∠A C、AB2+BC2=AC2 D、⊙A与AC的交点是AC中点11. 已知在 中, , 是 的中点, 的延长线上的点 满足 . 的内切圆与边 , 的切点分别为 , ,延长 分别与 , 的延长线交于 , ,则 ( )A、0.5 B、1 C、1.5 D、212. 如图,在△ABC中,∠A=50°,内切圆I与边BC、CA、AB分别相切于点D、E、F,则∠EDF的度数为( )
A、∠A=50°,∠C=40° B、∠B﹣∠C=∠A C、AB2+BC2=AC2 D、⊙A与AC的交点是AC中点11. 已知在 中, , 是 的中点, 的延长线上的点 满足 . 的内切圆与边 , 的切点分别为 , ,延长 分别与 , 的延长线交于 , ,则 ( )A、0.5 B、1 C、1.5 D、212. 如图,在△ABC中,∠A=50°,内切圆I与边BC、CA、AB分别相切于点D、E、F,则∠EDF的度数为( )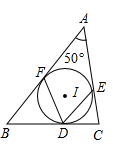 A、55° B、60° C、65° D、70°13. 如图,以点P为圆心,以下列选项中的线段的长为半径作圆,所得的圆与直线l相切的是( )
A、55° B、60° C、65° D、70°13. 如图,以点P为圆心,以下列选项中的线段的长为半径作圆,所得的圆与直线l相切的是( ) A、PA B、PB C、PC D、PD14. 若 的半径 ,点O到直线 的距离为3,下列图中位置关系正确的是( )A、
A、PA B、PB C、PC D、PD14. 若 的半径 ,点O到直线 的距离为3,下列图中位置关系正确的是( )A、 B、
B、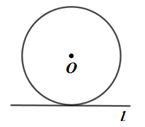 C、
C、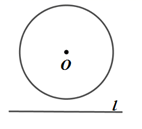 D、
D、 15. 在△ABC中,I是内心,∠BIC=130°,则∠A的度数是( )A、40° B、50° C、65° D、80°16. 以坐标原点 为圆心,1为半径作圆,直线 与 相交,则 的取值范围是( )A、 B、 C、 D、17. 如图,在平面直角坐标系中,以原点O为圆心,3为半径的半圆,直线AB:y=x+b与x轴交于点P(x , 0),若直线AB与半圆弧有公共点,则x值的范围是( )
15. 在△ABC中,I是内心,∠BIC=130°,则∠A的度数是( )A、40° B、50° C、65° D、80°16. 以坐标原点 为圆心,1为半径作圆,直线 与 相交,则 的取值范围是( )A、 B、 C、 D、17. 如图,在平面直角坐标系中,以原点O为圆心,3为半径的半圆,直线AB:y=x+b与x轴交于点P(x , 0),若直线AB与半圆弧有公共点,则x值的范围是( )
 A、﹣3≤x≤3 B、﹣3≤x≤3 C、﹣3 ≤x≤3 D、0≤x≤318. 已知圆的直径为10 cm,圆心到直线l的距离为5 cm,那么直线l和这个圆的公共点有( )A、0个 B、1个 C、2个 D、1个或2个19. 已知半径为10的⊙O和直线l上一点A,且 ,则直线l与⊙O的位置关系是( )A、相切 B、相交 C、相交或相离 D、相切或相交20. 已知圆O的直径为12 ,圆心到直线 的距离为6 ,则直线 与圆O的公共点的个数为( )A、2 B、1 C、0 D、不确定21. 平面直角坐标系中, 的圆心坐标为 ,半径为5,那么 与 轴的位置关系是( )A、相交 B、相离 C、相切 D、以上都不是
A、﹣3≤x≤3 B、﹣3≤x≤3 C、﹣3 ≤x≤3 D、0≤x≤318. 已知圆的直径为10 cm,圆心到直线l的距离为5 cm,那么直线l和这个圆的公共点有( )A、0个 B、1个 C、2个 D、1个或2个19. 已知半径为10的⊙O和直线l上一点A,且 ,则直线l与⊙O的位置关系是( )A、相切 B、相交 C、相交或相离 D、相切或相交20. 已知圆O的直径为12 ,圆心到直线 的距离为6 ,则直线 与圆O的公共点的个数为( )A、2 B、1 C、0 D、不确定21. 平面直角坐标系中, 的圆心坐标为 ,半径为5,那么 与 轴的位置关系是( )A、相交 B、相离 C、相切 D、以上都不是二、填空题
-
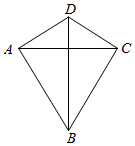
22. 圆的直径是 ,如果圆心与直线的距离是 ,那么该直线和圆的位置关系是.23. 已知 的半径3cm,圆心O到直线 的距离7cm,则直线 与 的位置关系是.24. 如图,在四边形 中, .若 ,则 的内切圆面积(结果保留 ).
 25. 已知△ABC中,⊙I为△ABC的内切圆,切点为H,若BC=6,AC=8,AB=10,则点A到圆上的最近距离等于 .
25. 已知△ABC中,⊙I为△ABC的内切圆,切点为H,若BC=6,AC=8,AB=10,则点A到圆上的最近距离等于 .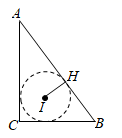 26. 一个直角三角形的两条直角边长分别为6cm、8cm,则它的内切圆的半径为cm.27. 如图,利用垂直于地面的墙面和刻度尺,可以度量出圆的半径为cm.
26. 一个直角三角形的两条直角边长分别为6cm、8cm,则它的内切圆的半径为cm.27. 如图,利用垂直于地面的墙面和刻度尺,可以度量出圆的半径为cm. 28. 已知⊙O的半径为 ,圆心O到直线L的距离为 ,则直线L与⊙O的位置关系是 .29. 如图,AB是⊙O的直径,点C在⊙O上,过点C的切线与BA的延长线交于点D,点E在弧BC上(不与点B,C重合),连接BE,CE.若∠D=40°,则∠BEC=度.
28. 已知⊙O的半径为 ,圆心O到直线L的距离为 ,则直线L与⊙O的位置关系是 .29. 如图,AB是⊙O的直径,点C在⊙O上,过点C的切线与BA的延长线交于点D,点E在弧BC上(不与点B,C重合),连接BE,CE.若∠D=40°,则∠BEC=度.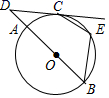 30. 《九章算术》是我国古代内容极为丰富的数学名著.书中有下面问题“今有勾八步,股十五步,问勾中容圆径几何.”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”.请你计算其结果为步.31. 已知 的两直角边分别是6和8,则其内切圆半径为 .32. 已知圆的直径是 圆心到直线 的距离是 ,那么直线 与该圆的位置关系是 .33. 已知⊙O的半径为3,圆心O到直线l的距离为m , 若m满足方程 ,则⊙O与直线l的位置关系是34. 如图,在△ABC中,AC=6cm,BC=8cm,AB=10cm,则△ABC内切圆的半径为cm.
30. 《九章算术》是我国古代内容极为丰富的数学名著.书中有下面问题“今有勾八步,股十五步,问勾中容圆径几何.”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”.请你计算其结果为步.31. 已知 的两直角边分别是6和8,则其内切圆半径为 .32. 已知圆的直径是 圆心到直线 的距离是 ,那么直线 与该圆的位置关系是 .33. 已知⊙O的半径为3,圆心O到直线l的距离为m , 若m满足方程 ,则⊙O与直线l的位置关系是34. 如图,在△ABC中,AC=6cm,BC=8cm,AB=10cm,则△ABC内切圆的半径为cm.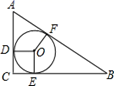 35. 如图,△ABC中,∠A=60°,若O为△ABC的内心,则∠BOC的度数为度.
35. 如图,△ABC中,∠A=60°,若O为△ABC的内心,则∠BOC的度数为度.
三、解答题
-
36. 如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O分别交CA,CB于点E,F,点G是AD的中点.求证:GE是⊙O的切线.

四、综合题
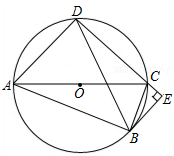
-
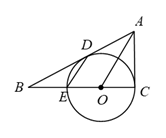
37. 如图,AB与⊙O相切于点B , AO交⊙O于点C , AO的延长线交⊙O于点D , E是 上不与B , D重合的点,sinA= .
 (1)、求∠DEB的度数;(2)、若⊙O的半径为2,点F在AB的延长线上,且BF=2 ,求证:DF与⊙O相切.38. 如图,以线段AB为直径的⊙O交线段AC于点E,点M是弧AE的中点,OM交AC于点D,∠BOE=60°,∠C=60°,BC=2 .
(1)、求∠DEB的度数;(2)、若⊙O的半径为2,点F在AB的延长线上,且BF=2 ,求证:DF与⊙O相切.38. 如图,以线段AB为直径的⊙O交线段AC于点E,点M是弧AE的中点,OM交AC于点D,∠BOE=60°,∠C=60°,BC=2 . (1)、求证:BC是⊙O的切线;(2)、求MD的长度.
(1)、求证:BC是⊙O的切线;(2)、求MD的长度.
-