初中数学浙教版八年级下学期期末复习专题11 三角形的中位线定理
试卷更新日期:2021-06-21 类型:复习试卷
一、单选题
-
1. 如图,点D和点E分别是BC和BA的中点,已知AC=4,则DE为( )
 A、1 B、2 C、4 D、82. 如图,在 中,点 , , 分别是边 , , 的中点,若 ,则四边形 的周长为( )
A、1 B、2 C、4 D、82. 如图,在 中,点 , , 分别是边 , , 的中点,若 ,则四边形 的周长为( ) A、1 B、2 C、4 D、83. 如图,在Rt△ABC中,∠ACB=90°,点D、E分别是AB、BC的中点,点F是BD的中点,若AB=5,则EF=( )
A、1 B、2 C、4 D、83. 如图,在Rt△ABC中,∠ACB=90°,点D、E分别是AB、BC的中点,点F是BD的中点,若AB=5,则EF=( ) A、 B、 C、 D、24. 已知三角形的三条中位线的长分别是 ,则这个三角形的周长为( )A、6.5 B、13 C、24 D、265. 如图,在 中, 平分 , 于点E,交 于点F,点G是 的中点,若 , ,则 的长为( ).
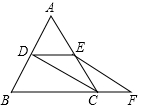
A、 B、 C、 D、24. 已知三角形的三条中位线的长分别是 ,则这个三角形的周长为( )A、6.5 B、13 C、24 D、265. 如图,在 中, 平分 , 于点E,交 于点F,点G是 的中点,若 , ,则 的长为( ). A、 B、 C、 D、6. 如图, 的对角线 与 相交于点O,且 .若E是 边的中点, , ,则 的长为( )
A、 B、 C、 D、6. 如图, 的对角线 与 相交于点O,且 .若E是 边的中点, , ,则 的长为( )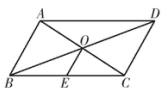 A、 B、 C、 D、7. 如图是一块等腰三角形空地ABC,已知点D,E分别是边AB,AC的中点,量得AC=12米,AB=BC=8米,若用篱笆围成四边形BCED,则需要篱笆的长是( )
A、 B、 C、 D、7. 如图是一块等腰三角形空地ABC,已知点D,E分别是边AB,AC的中点,量得AC=12米,AB=BC=8米,若用篱笆围成四边形BCED,则需要篱笆的长是( ) A、22米 B、20米 C、17米 D、14米8. 如图,在四边形 中,点P是边 上的一个动点,点Q是边 上的一个定点,连接 和 ,点E和F分别是 和 的中点,则随着点P的运动,线段 的长( )
A、22米 B、20米 C、17米 D、14米8. 如图,在四边形 中,点P是边 上的一个动点,点Q是边 上的一个定点,连接 和 ,点E和F分别是 和 的中点,则随着点P的运动,线段 的长( ) A、逐渐变大 B、逐渐变小 C、先变小再变大 D、始终不变9. 如图,要测定被池塘隔开的A,B两点的距离,可以在AB外选一点C,连接AC,BC,并分别找出它们的中点D,E,连接ED.现测得AC=42m,BC=64m,DE=26m,则AB等于( )
A、逐渐变大 B、逐渐变小 C、先变小再变大 D、始终不变9. 如图,要测定被池塘隔开的A,B两点的距离,可以在AB外选一点C,连接AC,BC,并分别找出它们的中点D,E,连接ED.现测得AC=42m,BC=64m,DE=26m,则AB等于( ) A、42m B、52m C、56m D、64m10. 如图,在四边形ABCD中,P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠EPF=140°,则∠EFP的度数是( )
A、42m B、52m C、56m D、64m10. 如图,在四边形ABCD中,P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠EPF=140°,则∠EFP的度数是( )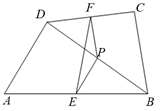 A、50° B、40° C、30° D、20°
A、50° B、40° C、30° D、20°二、填空题
-
11. 如图,任意四边形ABCD各边中点分别是E , F , G , H , 若对角线AC , BD的长都为10 cm , 则四边形EFGH的周长是cm .
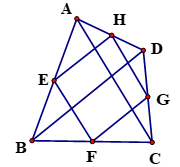 12. 如图,在菱形ABCD中,E、F分别是AC、BC的中点,如果EF=5,那么菱形ABCD的周长 .
12. 如图,在菱形ABCD中,E、F分别是AC、BC的中点,如果EF=5,那么菱形ABCD的周长 . 13. 如图,在平行四边形ABCD中,对角线AC与BD相交于点O,点E为BC边的中点,连接OE,若AB=4 ,则线段OE的长为 .
13. 如图,在平行四边形ABCD中,对角线AC与BD相交于点O,点E为BC边的中点,连接OE,若AB=4 ,则线段OE的长为 . 14. 如图,△ABC的面积是16,点D,E,F,G分别是BC,AD,BE,CE的中点,则△AFG的面积是 .
14. 如图,△ABC的面积是16,点D,E,F,G分别是BC,AD,BE,CE的中点,则△AFG的面积是 .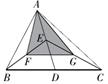 15. 在四边形ABCD中,对角线AC ⊥BD且AC=4,BD=8,E、F分别是边AB.CD的中点,则EF= .
15. 在四边形ABCD中,对角线AC ⊥BD且AC=4,BD=8,E、F分别是边AB.CD的中点,则EF= .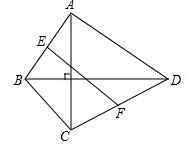 16. 如图,在 中,已知 依次连接 的三边中点, 得 ,再依次连接 的三边中点得 ,···,则 的周长为 .
16. 如图,在 中,已知 依次连接 的三边中点, 得 ,再依次连接 的三边中点得 ,···,则 的周长为 .
三、解答题
-
17. 如图,△ABC中,点D、E分别为AB、AC的中点,连接DE,线段BE、CD相交于点O,若OD=2,求OC的长.
 18. 已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点,判断四边形MENF是什么特殊平行四边形,并证明你的结论.
18. 已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点,判断四边形MENF是什么特殊平行四边形,并证明你的结论. 19. 如图,四边形ABCD是菱形,E、F、G、H分别是边AB、BC、CD、DA的中点,连接EF、FG、GH、HE.求证:四边形EFGH是矩形.
19. 如图,四边形ABCD是菱形,E、F、G、H分别是边AB、BC、CD、DA的中点,连接EF、FG、GH、HE.求证:四边形EFGH是矩形.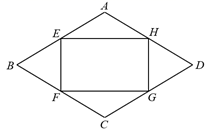 20. 我们定义:连接凸四边形一组对边中点的线段叫做四边形的“准中位线”.
20. 我们定义:连接凸四边形一组对边中点的线段叫做四边形的“准中位线”. (1)、概念理解:如图1,四边形ABCD中,F为CD的中点,∠ADB=90°,E是AB边上一点,满足DE=AE,试判断EF是否为四边形ABCD的准中位线,并说明理由.(2)、问题探究:如图2,△ABC中,∠ACB=90°,AC=6,BC=8,动点E以每秒1个单位的速度,从点A出发向点C运动,动点F以每秒6个单位的速度,从点C出发沿射线CB运动,当点E运动至点C时,两点同时停止运动.D为线段AB上任意一点,连接并延长CD,射线CD与点A,B,E,F构成的四边形的两边分别相交于点M,N,设运动时间为t.问t为何值时,MN为点A,B,E,F构成的四边形的准中位线.(3)、应用拓展:如图3,EF为四边形ABCD的准中位线,AB=CD,延长FE分别与BA,CD的延长线交于点M,N,请找出图中与∠M相等的角并证明.21. 如图,在 中, ,D为CA延长线上一点, 于点E,交AB于点F.
(1)、概念理解:如图1,四边形ABCD中,F为CD的中点,∠ADB=90°,E是AB边上一点,满足DE=AE,试判断EF是否为四边形ABCD的准中位线,并说明理由.(2)、问题探究:如图2,△ABC中,∠ACB=90°,AC=6,BC=8,动点E以每秒1个单位的速度,从点A出发向点C运动,动点F以每秒6个单位的速度,从点C出发沿射线CB运动,当点E运动至点C时,两点同时停止运动.D为线段AB上任意一点,连接并延长CD,射线CD与点A,B,E,F构成的四边形的两边分别相交于点M,N,设运动时间为t.问t为何值时,MN为点A,B,E,F构成的四边形的准中位线.(3)、应用拓展:如图3,EF为四边形ABCD的准中位线,AB=CD,延长FE分别与BA,CD的延长线交于点M,N,请找出图中与∠M相等的角并证明.21. 如图,在 中, ,D为CA延长线上一点, 于点E,交AB于点F. (1)、求证: 是等腰三角形;(2)、若 , ,求线段DE的长.22. 如图,平行四边形 的对角线交于点O,以 , 为邻边作平行四边形 , 交 于点F,连结 .
(1)、求证: 是等腰三角形;(2)、若 , ,求线段DE的长.22. 如图,平行四边形 的对角线交于点O,以 , 为邻边作平行四边形 , 交 于点F,连结 .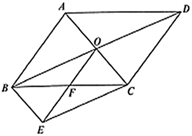 (1)、求证:F为 中点;(2)、若 , ,求平行四边形 的周长.
(1)、求证:F为 中点;(2)、若 , ,求平行四边形 的周长.