初中数学苏科版九年级上册1.1-1.2一元二次方程及求解同步练习

试卷更新日期：2021-06-21 类型：同步测试

进入出卷网下载

一、单选题

1. 用配方法解方程x²+4x+1＝0时，配方结果正确的是（）

A、（x﹣2）²＝5 B、（x﹣2）²＝3 C、（x+2）²＝5 D、（x+2）²＝3

查看试题解析
2. 将关于 $x$ 的一元二次方程 $x^{2} ﹣ p x + q = 0$ 变形为 $x^{2} = p x - q$ ，就可以将 $x^{2}$ 表示为关于 $x$ 的一次多项式，从而达到“降次”的目的，又如 $x^{3} = x \cdot x^{2} = x (p x ﹣ q) =$ …，我们将这种方法称为“降次法”，通过这种方法可以化简次数较高的代数式．根据“降次法”，已知： $x^{2} - x - 1 = 0$ ，且 $x > 0$ ，则 $x^{3} + 1$ 的值为（）

A、 $1 + \sqrt{5}$ B、 $1 - \sqrt{5}$ C、 $3 ﹣ \sqrt{5}$ D、 $3 + \sqrt{5}$

查看试题解析
3. 在平面直角坐标系xOy中，对于横、纵坐标相等的点称为“好点”．下列函数的图象中不存在“好点”的是（）

A、y＝﹣x B、y＝x+2 C、y $= \frac{2}{x}$ D、y＝x²﹣2x

查看试题解析
4. 若关于x的一元二次方程(k-1)x²+2x-2=0有实数根，则k的取值可能是（）

A、-2 B、0 C、 $\frac{1}{2}$ D、1

查看试题解析
5. 一元二次方程 $4 x^{2} - 4 x - 3 = 0$ 配方后可化为（）

A、 ${(x + \frac{1}{2})}^{2} = 1$ B、 ${(x - \frac{1}{2})}^{2} = 1$ C、 ${(x + \frac{1}{2})}^{2} = \frac{3}{4}$ D、 ${(x - \frac{1}{2})}^{2} = \frac{3}{4}$

查看试题解析
6. 若关于x的一元二次方程kx²﹣x﹣ $\frac{3}{4}$ ＝0有实数根，则实数k的取值范围是（　　）

A、k＝0 B、k≥ $- \frac{1}{3}$ C、k≥ $- \frac{1}{3}$ 且k≠0 D、k＞ $- \frac{1}{3}$

查看试题解析
7. 一元二次方程x（x﹣2）＝x﹣2的根是（　　）

A、x＝2 B、x₁＝0，x₂＝2 C、x₁＝2，x₂＝1 D、x＝﹣1

查看试题解析
8. 已知y＝kx+k﹣1的图象如图所示，则关于x的一元二次方程x²﹣x﹣k²﹣k＝0的根的情况是（）

A、无实数根 B、有两个相等或不相等的实数根 C、有两个不相等的实数根 D、有两个相等的实数根

查看试题解析
9. 已知 $x_{1}$ 、 $x_{2}$ 是关于 $x$ 的方程 $x^{2} - 2 x - m^{2} = 0$ 的两根，下列结论中不一定正确的是（）

A、 $x_{1} + x_{2} > 0$ B、 $x_{1} \cdot x_{2} < 0$ C、 $x_{1} \neq x_{2}$ D、方程必有一正根

查看试题解析
10. 一元二次方程 $2021 x^{2} - x + 2021 = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定

查看试题解析
11. 方程 $x^{3} - 4 x = 0$ 的解是（）

A、2或0 B、±2或0 C、2 D、－2或0

查看试题解析
12. 已知关于x的一元二次方程 $x^{2} - 2 \sqrt{6} x + k = 0$ 有两个相等的实数根，则k的值为（）

A、3 B、 $\pm 6$ C、6 D、 $\pm 3$

查看试题解析
13. 关于x的一元二次方程 $x^{2} - 3 x + m = 0$ 有两个不相等的实数根，则实数m的取值范围为（）

A、 $m > \frac{9}{4}$ B、 $m < - \frac{9}{4}$ C、 $m \leq - \frac{9}{4}$ D、 $m < \frac{9}{4}$

查看试题解析
14. 关于x的方程 $x^{2} ﹣ 2 x + a = 0$ （a为常数）无实数根，则点 $(a ， a + 1)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
15. 若关于x的一元二次方程x²﹣2（k﹣2）x+k²+2k＝0有两个实数根x₁ ， x₂ ，则k的最大整数值为（　　）

A、2 B、1 C、0 D、不存在

查看试题解析
16. 关于x的方程（x﹣1）（x+2）＝m²（m为常数）的根的情况，下列结论中正确的是（　　）

A、两个不相等实数根 B、两个相等实数根 C、没有实数根 D、无法判断根的情况

查看试题解析
17. 下列方程中属于一元二次方程的是（）

A、 $2 {(x + 1)}^{2} = x + 1$ B、 $\frac{1}{x^{2}} + \frac{1}{x} = 0$ C、 $a x^{2} + b x + c = 0$ D、 $x (x + 3) = x^{2} - 2$

查看试题解析
18. 关于 $x$ 的一元二次方程 $(a - 6) x^{2} - 8 x + 6 = 0$ 有实数根，则满足条件的正整数 $a$ 的个数是（）

A、6 B、7 C、8 D、9

查看试题解析
19. 用配方法解方程x²﹣10x﹣1＝0时，变形正确的是（　　）

A、（x﹣5）²＝24 B、（x﹣5）²＝26 C、（x+5）²＝24 D、（x+5）²＝26

查看试题解析
20. 若一元二次方程 $2 x^{2} - m x + 1 = 0$ 有两个不相等的实数根，则m的值可以是（）

A、3 B、2 C、1 D、0

查看试题解析

二、填空题

21. 数学活动课上，小云和小王在讨论张老师出示的一道代数式求值问题：

已知实数a，b同时满足a²+2a＝b+2，b²+2b＝a+2，求代数式 $\frac{b}{a} + \frac{a}{b}$ 的值．

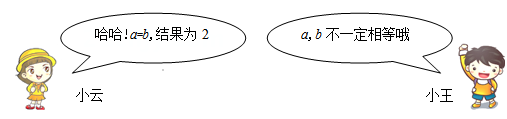
结合他们的对话，请解答下列问题：

(1)、当a＝b时，a的值是．

(2)、当a≠b时，代数式

\frac{b}{a} + \frac{a}{b}

的值是．

查看试题解析

22. 关于x的一元二次方程2x²﹣4x+m $- \frac{3}{2} =$ 0有实数根，则实数m的取值范围是．

查看试题解析
23. 如果关于x的一元二次方程kx²﹣3x+1=0有两个实数根，那么k的取值范围是．

查看试题解析
24. 已知 $x = 1$ 是方程 $x^{2} + b x - 2 = 0$ 的一个根，则方程的另一个根是．

查看试题解析
25. 若一元二次方程x²-6x+c=0有两个相等的实数根，则c=

查看试题解析
26. 已知a是方程x²+3x﹣4＝0的根，则代数式2a²+6a+4的值是．

查看试题解析
27. 一元二次方程x²﹣c＝0的一个根是2，则常数c的值是．

查看试题解析
28. 若关于x的一元二次方程x²-4x-k=0有两个不相等的实数根，则k的值可以为．（写出一个即可）

查看试题解析
29. 若关于x的一元二次方程x²-2x+c=0没有实数根．则实数c取值范围是

查看试题解析
30. 把一元二次方程5x（x-3）=6-2x化成一般形式后常数项是

查看试题解析
31. 若方程 $a x^{2} + b x + c = 0 (a \neq 0)$ ，满足 $3 a - b + \frac{1}{3} c = 0$ 则方程必有一根为．

查看试题解析
32. 若关于x的一元二次方程 $x^{2} + x - m = 0$ 有两个实数根，则m的取值范围是．

查看试题解析
33. 若关于x的一元二次方程 $x^{2} + 2 (m + 1) x + c = 0$ 有两个相等的实数根，则c的最小值是．

查看试题解析

三、计算题

34. 解方程： $\frac{1}{2}$ x²﹣x﹣1＝0．

查看试题解析

四、解答题

35. 小敏与小霞两位同学解方程3（x﹣3）＝（x﹣3）²的过程如下框：

小敏：

两边同除以（x﹣3），得

3＝x﹣3，

则x＝6．

小霞：

移项，得3（x﹣3）﹣（x﹣3）²＝0，

提取公因式，得（x﹣3）（3﹣x﹣3）＝0．

则x﹣3＝0或3﹣x﹣3＝0，

解得x₁＝3，x₂＝0．

你认为他们的解法是否正确？若正确请在框内打“√”；若错误请在框内打“×”，并写出你的解答过程．