初中数学苏科版八年级上册6.4 一次函数的实际应用 同步练习
试卷更新日期：2021-06-21 类型：同步测试
一、单选题
-
1. 把一个长为8，宽为3的长方形的宽增加x（0≤x＜5），长不变，所得长方形的面积y关于x的函数表达式为（ ）A、y＝24﹣x B、y＝8x﹣24 C、y＝8x D、y＝8x+242. 杆秤是我国传统的计重工具.如图，可以用秤砣到秤纽的水平距离，来得出秤钩上所挂物体的质量.称重时，若秤砣到秤纽的水平距离为x（单位：cm）时，秤钩所挂物重为y（单位：kg），则y是x的一次函数.下表记录了四次称重的数据，其中只有一组数据记录错误，它是（ ）
组数
1
2
3
4
x/cm
1
2
4
7
y/kg
0.80
1.05
1.65
2.30
A、第1组 B、第2组 C、第3组 D、第4组3. 为增强居民节水意识，我市自来水公司采用以户为单位分段计费办法收费，即每月用水不超过10吨，每吨收费 元；若超过10吨，则10吨水按每吨 元收费，超过10吨的部分按每吨 元收费，公司为居民绘制的水费 （元）与当月用水量 （吨）之间的函数图象如下，则下列结论错误的是（ ）
A、 B、 C、若小明家3月份用水14吨，则应缴水费23元 D、若小明家7月份缴水费30元，则该用户当月用水 吨4. 如图，某电信公司提供了A，B两种方案的移动通讯费用y（元）与通话时间x（元）之间的关系，则下列结论中正确的有（ ）
（1）若通话时间少于120分，则A方案比B方案便宜20元；（2）若通话时间超过200分，则B方案比A方案便宜12元；（3）若通讯费用为60元，则B方案比A方案的通话时间多；（4）若两种方案通讯费用相差10元，则通话时间是145分或185分.
A、1个 B、2个 C、3个 D、4个二、填空题
-
5. 甲，乙两车从 城出发前往 城．在整个行程中，甲，乙两车都以匀速行驶，汽车离开 城的距离 与时刻 的对应关系如图所示．
请根据相关信息，解答下列问题：
(1)、填表：从 城出发的时刻
到达 城的时刻
甲
5：00
乙
9：00
(2)、填空：① ， 两城的距离为 ；
②甲车的速度为 ，乙车的速度为 ；
③乙车追上甲车用了 ，此时两车离开 城的距离是 ；
④当9：00时，甲乙两车相距 ；
⑤当甲车离开 城 时，甲车行驶了 ；
⑥当乙车出发行驶 时，甲乙两车相距 ．
6. 某店家进一批应季时装共400件，要在六周内卖完，每件时装成本500元．前两周每件按1000元标价出售，每周只卖出20件．为了将时装尽快销售完，店家进行了一次调查并得出每周时装销售数量与时装价格折扣的关系如下：价格折扣
原价
9折
8折
7折
6折
5折
每周销售数量（单位：件）
20
25
40
90
100
150
为盈利最大，店家选择将时装打折销售，后四周最多盈利元．
7. 星期天小明步行从家去图书馆，中间要路过超市，小明以a米/分钟的速度匀速到达超市，再以b米/分钟的速度匀速到达图书馆，图中的折线 反映了小明从家步行到图书馆所走的路程s（米）与时间t（分钟）的函数关系，根据图象提供的信息， 的值为 ．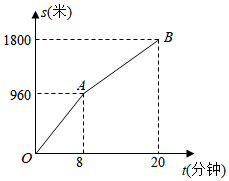
8. 甲、乙两人分别从A、B两地出发，相向而行．图中的 ， 分别表示甲、乙离B地的距离 与甲出发后所用时间 的函数关系图象，则甲出发小时与乙相遇．
9. 小张、小王两个人从甲地出发，去8千米外的乙地，图中线段OA、PB分别反映了小张、小王步行所走的路程S（千米）与时间t（分钟）的函数关系，根据图象提供的信息，小王比小张早到乙地的时间是分钟．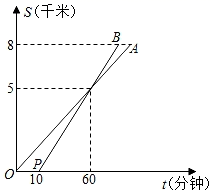
三、解答题
-
10. 世界上大部分国家都使用摄氏温度，但美国、英国等国家的天气预报仍然使用华氏温度．两种计量之间有如下对应：
摄氏温度/℃
0
10
20
30
40
华氏温度/℉
32
50
68
86
104
（Ⅰ）如果两种计量之间的关系是一次函数，设摄氏温度为x（℃）时对应的华氏温度为y（℉），请你写出华氏温度关于摄氏温度的函数表达式；
（Ⅱ）求当华氏温度为0℉时，摄氏温度是多少℃？
（Ⅲ）华氏温度的值与对应的摄氏温度的值有可能相等吗？若可能，求出此值；若不可能，请说明理由．
11. 兰州市居民用电现有两种用电收费方式：智能分时电表
普通电表
峰时（8：00﹣22：00）
谷时（22：00﹣次日8：00）
电价0.51/千瓦时
电价0.76元/千万时
电价0.26元/千瓦时
设某家庭某月用电总量为x千瓦时，其中谷时用电60千瓦时，则峰时用电（x﹣60）千瓦时，智能分时电表计价时的总价为为y1（元），普通电表计价时的总价为y2（元）.请分别写出两种电表计价时的总价与用电总量之间的函数关系式.
四、综合题
-
12. 李师傅将容量为60升的货车油箱加满后，从工厂出发运送一批物资到某地．行驶过程中，货车离目的地的路程s（千米）与行驶时间t（小时）的关系如图所示（中途休息、加油的时间不计．当油箱中剩余油量为10升时，货车会自动显示加油提醒．设货车平均耗油量为0.1升/千米，请根据图象解答下列问题：
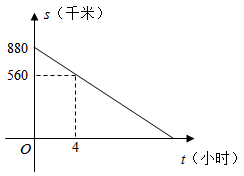(1)、直接写出工厂离目的地的路程；(2)、求s关于t的函数表达式；(3)、当货车显示加油提醒后，问行驶时间t在怎样的范围内货车应进站加油？13. 现代互联网技术的广泛应用，催生了快递行业的高速发展，小明计划给朋友快递一部分物品，经了解有甲乙两家快递公司比较合适．甲公司表示：快递物品不超过1千克的，按每千克22元收费；超过1千克，超过的部分按每千克15元收费，乙公司表示：按每千克16元收费，另加包装费3元，设小明快递物品x千克．(1)、根据题意，填写下表：快递物品重量（千克）
0.5
1
3
4
甲公司收费（元）
22
乙公司收费（元）
11
51
67
(2)、设甲快递公司收费 元，乙快递公司收费 元，分别写出 关于x的函数关系式；(3)、若小明在两家快递公司花费相同，则他的快递物品重量是千克；若他快递物品6千克，应选择快递公司（选填“甲”或“乙”）；
若他快递物品3.5千克，则选择快递公司（选填“甲”或“乙”）．
14. 某数学课外研究小组的同学们利用学校组织的校园义卖实践活动的机会，准备为社会献爱心。活动开始前，经过市场调查，他们分别按某超市售价的8折和7折从批发市场购进甲、乙两种智能文具盒共120个，活动当日按超市的同等售价卖出已知从批发市场购进甲种智能文具盒的单价是20元，购进乙种智能文具盒的单价是35元假设从批发市场购买甲种智能文具盒x个，两种智能文具盒全部销售完所获利润为y(元)。(1)、甲种智能文具盒的售价为元，乙种智能文具盒的售价为元；(2)、求y与x之间的函数关系式；(3)、若购进每种智能文具盒的数量不少于30个，则如何购进这两种文具盒可使得本次义卖获得最大利润，最大利润是多少？15. 甲、乙两车从A城出发匀速行驶至B城，在整个行驶过程中，甲、乙两车离开A城的距离)(千米)与甲车行驶时间x(小时)之间的函数关系如图所示，根据图象提供的信息，解决下列问题：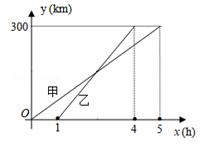
(1)、A，B两城相距千米；(2)、分别求甲、乙两车离开A城的距离y与x的关系式。(3)、求乙车出发后几小时追上甲车？16. 疫情期间，某企业为了保证能够尽快复工复产，准备为员工采购20000袋医用口罩.因为疫情期间口罩等物资紧缺，无法购买同型号的口罩，经市场调研，准备购买 、 、 三种型号的口罩，这三种型号口罩单价如表所示：型号
单价（元/袋）
30
35
40
若购买 型口罩的数量是 型的2倍，设购买 型口罩 袋，该企业购买口罩的总费用为 元.
(1)、请求出 与 的函数关系式；(2)、已知口罩生产厂家能提供的 型口罩的数量不大于 型口罩的数量，当购买 型口罩多少袋时购买口罩的总费用最少？并求最少总费用.17. 某早餐机开机后，自动启动程序：先匀速加热，当机内温度升高到 时，自动停止加热，同时机内温度匀速下降，当机内温度降至 时，早餐机又自动启动上述程序，直至关机.已知早餐机的机内初始温度为 ，降温温度是加热速度的2倍.早餐机的机内温度 与开机之后的时间 之间的函数关系部分图象如图所示.
(1)、早餐机的加热速度为 ；(2)、求线段 所表示的 与 之间的函数表达式；(3)、将食物放入该早餐机，自开机之后，要使机内温度不低于 的累计时间不少于 ，至少需要 .18. 今年小芳家3，4，5月总用电量是900千瓦时，其中3月用电量比4月少20千瓦时，5月用电量比4月多20千瓦时.(1)、求今年小芳家5月用电量.(2)、小芳家安装了“峰谷”电表，电费的收费标准如下表：电价(元/千瓦时)
第一档(月用电量在0到200千瓦时)
第二档(月用电量在201千瓦时到600千瓦时)
第三档(月用电量在601千瓦时以上)
高峰时段(8：00-22：00 )
0.53
0.58
0.83
低谷时段(其余时段)
0.3
0.35
0.6
预计今年6月“低谷时段”用电量是5月“低谷时段”用电量的2倍，6月“高峰时段”用电量是5月“高峰时段”用电量的 倍，设今年5月“低谷时段”用电量为x千瓦时，6月总用电量为m千瓦时.
①用含x的代数式表示m.
②若x≥300千瓦时，求今年小芳家6月电费的最小值.
19. 小军和爸爸同时从家骑自行车去图书馆，爸爸先以150米/分的速度骑行一段时间，休息了5分钟，再以m米/分的速度到达图书馆，小军始终以同一速度骑行，两人行驶的路程y（米）与时间x（分钟）的关系如图．请结合图象，解答下列问题：
(1)、a=；m= ．(2)、若小军的速度是120米/分，求小军在图中与爸爸第二次相遇时，距图书馆的距离．20. 将长为 的长方形白纸，按图中的方法粘合起来，粘合部分的宽为 .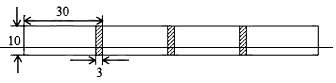
(1)、求5张白纸粘合后的长度.(2)、设x张白纸粘合后的长度为 ，写出y与x之间的关系式.并求当 时，y的值.21. 为全面落实乡村振兴总要求，充分发扬“为民服务孺子牛”“创新发展拓荒牛”“艰苦奋斗老黄牛”精神，某镇政府计划在该镇试种植苹果树和桔子树共100棵.已知平均每棵果树的投入成本和产量如表所示，且苹果的售价为10元/kg，桔子的售价为6元/kg.成本（元/棵）
产量（kg/棵）
苹果树
120
30
桔子树
80
25
设种植苹果树x棵.
(1)、若种植苹果树和桔子树共获利y元，求y与x之间的函数关系式；(2)、若种植苹果树45棵，求种植苹果树和桔子树共获利多少元？22. 西银高铁于2020年12月26日正式开通运营，从“千年古都”到“塞上江南”，由原来的14个小时变为3小时，沿途风景如画，尽显西北风情.试运行期间，一列动车从西安开往银川，到达目的地后停留一段时间，以原速返回西安，设动车从西安出发x（h），动车离西安的距离为y（km），y与x的函数关系如图所示.
(1)、求返回西安时y与x之间的函数关系式；(2)、求动车从西安出发5小时后离西安的距离.23. 4月23日是“世界读书日”，甲、乙两书店在这一天举行了购书优惠活动：甲书店：所有书籍按标价8折出售；乙书店：一次购书标价总额不超过100元的按原价计费，超过100元的部分打6折.设小红同学当天购书标价总额为x元，去甲书店付y甲元，去乙书店购书应付y乙元，其函数图象如图所示.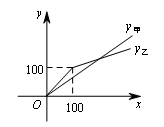
(1)、求y甲、y乙与x的关系式；(2)、两图象交于点A，请求出A点坐标，并说明点A的实际意义；(3)、请根据函数图象，直接写出小红选择去哪个书店购书更合算.24. 某市出租车计费方法如图所示，x(km)表示行驶里程，y(元)表示车费，请根据图象回答下列问题：
(1)、出租车的起步价是多少元？当x＞3时，求y关于x的函数关系式；(2)、若某乘客有一次乘出租车的车费为32元，求这位乘客乘车的里程.25. 时下少儿编程是一个很热门的项目，需要有良好的数学逻辑思维，某次由编程控制的两辆模型车沿同一路线同时从 点出发驶向 点，途中乙车按照程序设定停车一段时间，然后以一定的速度匀速驶向 点，甲车从 到 点速度始终保持不变，如图所示时甲、乙两车之间的距离 （分米）与两车出发时间 （分钟）的函数图象根据相关信息解答下列问题：
(1)、点 的坐标表示的实际意义是什么？(2)、求出 所表示的关系式，并写出乙车停车后再出发的速度.(3)、求停车前两车的速度以及 的值.26. 某图书馆现有2000本图书供学生借阅，如果每个学生借4本，请回答下列问题：(1)、请写出剩下的图书的数量y（本）与借书学生人数x之间的关系式．
(2)、求100个学生借书后图书馆剩下的图书数量．
27. 用充电器给某手机充电时，其屏幕的起始画面如图①.
经测试，在用快速充电器和普通充电器对该手机充电时，其电量E（单位：%）与充电时间t（单位：h）的函数图象分别为图②中的线段AB、AC.
根据以上信息，回答下列问题：
(1)、在目前电量20%的情况下，用充电器给该手机充满电时，快速充电器比普通充电器少用多少小时？(2)、求线段AB、AC对应的函数表达式；(3)、已知该手机正常使用时耗电量为每小时10%，在用快速充电器将其充满电后，正常使用ah，接着再用普通充电器将其充满电，其“充电﹣耗电﹣充电”的时间恰好是6h，求a的值.28. 周末小明和父母一起开车到距家200km的景点旅游，出发前，汽车油箱内储油45L ， 当行驶150km时，发现油箱余油量为30L ． （假设行驶过程中汽车的耗油量是均匀的）(1)、求该车平均每千米的耗油量，并写出行驶路程x（km）与剩余油量Q（L）的关系式；(2)、当x＝280时，求剩余油量Q ．29. 小王骑车从甲地到乙地，小李骑车从乙地到甲地，小王的速度小于小李的速度，两人同时出发，沿同一条公路匀速前进.图中的折线表示两人之间的距离y（km）与小王的行驶时间x（h）之间的函数关系.请你根据图象进行探究：
(1)、小王的速度是km/h，小李的速度是km/h；(2)、求线段BC所表示的y与x之间的函数表达式，并写出自变量x的取值范围.(3)、求当两人相距18千米时，小王行驶多少小时？30. 打车软件的出现很大程度上方便了我们的生活，其中“滴漓出行”是全球最大的站式多样化出行渠道，现了解到某市“滴滴快车”普通时段的最新收费标准见下表；里程/千米
收费/元
2千米以下（含2千米）
11.4
2千米以上，每增加1千米
1.95
(1)、求“滴滴快车”的收费y（元）与行驶的里程数x（千米）之间的函数关系式；(2)、上周一，李老师乘坐“滴滴快车”从家到学校的车费是15.3元，李老师家距离学校多少千米？已知王老师家距离学校1.8千米，求王老师乘坐“滴滴快车”从家到学校的车费.31. 甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发向乙地，轿车比货车晚出发1.5小时，如图，线段 表示货车离甲地的距离y（千米）与时间x（小时）之间的函数关系；折线 表示轿车离甲地的距离y（千米）与时间x（时）之间的函数关系，请根据图象解答下列问题.
(1)、轿车到达乙地时，求货车与甲地的距离.(2)、求线段 对应的函数表达式.(3)、在轿车行进过程中，轿车行驶多少时间，两车相距15千米.32. 为了巩固拓展脱贫攻坚成果，开启乡村振兴发展之门，某村合作社组织20辆汽车装运A、B两种土特产到外地销售，规定每辆汽车只能装运一种特产，且必须装满；装运每种特产的汽车不少于4辆．设用x辆汽车装运A特产，此次外销获得的利润为y ， 根据下表提供的信息，解答下列问题：土特产
A
B
每辆汽车装运量（吨）
5
4
每吨特产获利（万元）
0.6
0.8
(1)、求y与x之间的函数关系式，并写出自变量的取值范围；(2)、由于市场需要，将A特产每吨售价提高 万元，求该合作社应该怎样装运销售这批土特产，可获得最大利润，最大利润是多少？33. 某旅游团乘坐旅游中巴车以50千米/时的速度匀速从甲地到相距200千米的乙地旅游．行驶了80千米时，车辆出现故障，与此同时，得知这个情况的乙地旅行社立刻派出客车以80千米/时的速度前来接应．相遇后，旅游团用了18分钟从旅游中巴换乘到客车上，随后以v（千米/时）的速度匀速到达乙地．设旅游团离开甲地的时间为x（小时），旅游中巴车距离乙地的路程为y1（千米），客车在遇到旅游团前离开乙地的路程y2（千米）．(1)、若v＝80千米/时，①y1与x的函数表达式为 ．
②求y2与x的函数表达式，并写出x的取值范围．
(2)、设旅游团从甲地到乙地所用的总时间为T（小时），求T（小时）与v（千米/时）的函数关系式（不写v的取值范围）．(3)、旅游团要求到达时间比按原来的旅游中巴正常到达乙地的时间最多晚1个小时，问客车返回乙地的车速至少为每小时多少千米？34. 一辆轿车和一辆货车分别从甲、乙两地同时出发，匀速相向而行，两车相遇时轿车比货车多行驶了90千米．设行驶的时间为t（小时），两车之间的距离为s（千米），图中线段AB表示从两车发车至两车相遇这一过程中s与t之间的函数关系，根据图象提供的信息回答下列问题：
(1)、求s关于t的函数关系式；（不必写出定义域）(2)、求两车的速度．35. 为了预防“诺如病毒”，某校对专用教室采取“药熏”消毒．从开始消毒到结束，室内含药量y（毫克/立方米）与时间x（分）这两个变量之间的关系如图中折线OA﹣AB所示．
(1)、求20分钟至60分钟时间段之间的含药量y与时间x的函数解析式（不要求写定义域）；(2)、开始消毒后，消毒人员在某一时刻对该专用教室的含药量进行第一次检测，时隔半小时进行了第二次跟踪检测，发现室内含药量比第一次检测时的含药量下降了2毫克/立方米，求第一次检测时的含药量．36. 甲、乙两家超市以相同的价格出售同样的商品，为了吸引顾客，各自推出不同的优惠方案：在甲超市累计购买商品超出300元之后，超出部分按原价8折优惠；在乙超市累计购买商品超出200元之后，超出部分按原价8.5折优惠．设顾客预计累计购物x元（x＞300），甲超市购物所付的费用为y1元，乙超市购物所付的费用为y2元．(1)、甲超市购物所付的费用y1与x的函数关系为：；乙超市购物所付的费用y2与x的函数关系为：；(2)、顾客应该如何选择购买会更省钱？37. 如图，一辆货车和一辆轿车先后从甲地开往乙地，线段 表示货车离开甲地的距离 与时间 之间的函数关系；折线 表示轿车离开甲地的距离 与时间 之间的函数关系，请根据图象解答下列问题：
(1)、求线段 所在直线的函数表达式.(2)、货车出发多长时间两车相遇？此时两车距离乙地多远？38. 如图，OA、BC分别是普通列车和动车从甲地开往乙地的路程 与时间 的函数图象，请根据图中的信息，解答下列问题：
(1)、根据图象信息，普通列车比动车早出发h，动车的平均速度是 ；(2)、分别求出OA、BC的函数表达式，并写出自变量x的取值范围；(3)、动车出发多少小时追上普通列车？此时他们距离出发地多少千米？39. 如图1所示，在A，B两地之间有汽车站C站，客车由A地驶往B地，货车由B地驶往C站.两车同时出发，匀速行驶.图2是客车、货车离C站的路程y1、y2（千米）与行驶时间x（小时）之间的函数关系图象.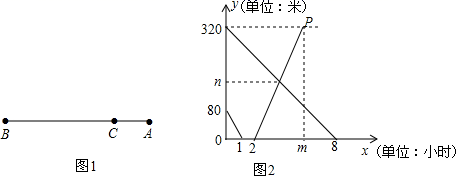
(1)、填空：A，B两地相距千米，图2中的m的值为；(2)、求两小时后，客车离C站的路程y2与行驶时间x之间的函数关系式；(3)、指出图2中n的实际意义，并求出n的值.40. 工厂某车间需加工一批零件，甲组工人加工中因故停产检修机器一次，然后以原来的工作效率继续加工，由于时间紧任务重，乙组工人也加入共同加工零件.设甲组加工时间t（时），甲组加工零件的数量为 （个），乙组加工零件的数量为 （个），其函数图象如图所示.
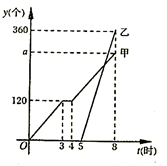(1)、求 与t之间的函数关系式，并写出t的取值范围；(2)、求a的值，并说明a的实际意义；(3)、甲组加工多长时间时，甲、乙两组加工零件的总数为480个.