初中数学浙教版八年级下学期期末复习专题9 平行四边形性质与判定
试卷更新日期：2021-06-21 类型：复习试卷
一、单选题
-
1. 如图，在 ABCD中，AB=5，AD=7，则 ABCD的周长为（ ）
A、12 B、14 C、35 D、242. 如图，点A是直线l外一点，在l上取两点B ， C ， 分别以A ， C为圆心，BC ， AB长为半径画弧，两弧相交于点D ， 分别连接AB ， AD ， CD ， 则四边形ABCD的（ ）
A、四条边相等 B、四个角相等 C、对角线互相垂直 D、对角线互相平分3. 下列命题正确的是（ ）A、一组对边平行、一组对角相等的四边形是平行四边形 B、一组对边平行、另一组对边相等的四边形是平行四边形 C、对角线相等的四边形是平行四边形 D、平行四边形的对角线将平行四边形分成四个全等的三角形4. 在□ ABCD中，∠A：∠B：∠C：∠D的值可以是（ ）A、2：1：2：1 B、1：2：2：1 C、1：1：2：2 D、1：2：3：45. 如图所示，在平行四边形ABCD中，已知AD=5cm，AB=3cm，AE平分∠BAD交BC边于点E，则EC等于（ ）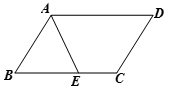
A、2 cm B、3 cm C、4 cm D、5 cm6. 在平面直角坐标系中，点A ， B ， C的坐标分别为 ， ， ，当四边形ABCD是平行四边形时，点D的坐标为（ ）A、 B、 C、 D、7. 如图，在平行四边形ABCD中，对角线AC，BD相交于O，AC＝10cm，AB＝4cm，BD⊥AB，则BD的长为（ ）
A、4cm B、.5cm C、6cm D、.8cm8. 如图所示，在四边形ABCD中，AD∥BC，要使四边形ABCD成为平行四边形还需要条件（ ）
A、AB＝DC B、∠1＝∠2 C、∠D＝∠B D、AB＝AD9. 如图，在四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定四边形ABCD为平行四边形的是（ ）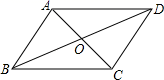
A、AB∥CD，AD∥BC B、AD∥BC，AB＝CD C、OA＝OC，OB＝OD D、AB＝CD，AD＝BC10. 如图，四边形ABCD中，AD∥BC，∠ABC+∠DCB=90°，且BC=2AD，以AB、BC、DC为边向外作正方形，其面积分别为 、 、 ，若 =3， =8，则 的值为（ ）
A、22 B、24 C、44 D、48二、填空题
-
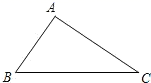
11. 如图，已知△ABC中，∠B=50°，分别以A，C为圆心，BC，AB长为半径画弧，两弧在直线BC上方交于点D，连接AD，CD，则∠D=.
12. 平行四边形的周长为24cm ， 相邻两边长的比为3︰1，那么这个平行四边形较短的边长为cm ．13. 如图平行四边形 ABCD 中，AE ^ BC于E ，AF ^ DC于 F，BC=5，AB=4，AE=3，则 AF的长为 ．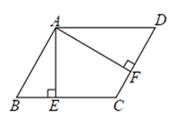
14. 如图，在 中， ，D是BC上的任一点， 交AC于点E， 交AB于点F那么四边形AFDE的周长是 ．
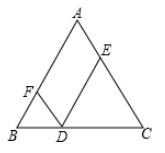15. 如图，平行四边形ABCD的对角线AC，BD交于点O，E，F是对角线AC上两点，给出下列4个条件：① ；②DE=BF；③ ；④ ，其中不能判定四边形DEBF是平行四边形的是；
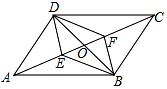16. 在平面直角坐标系中，A（﹣1，1），B（2，3），C（3m ， 4m+1），D在x轴上，若以A ， B ， C ， D四点为顶点的四边形是平行四边形，求点D的坐标.三、解答题
-
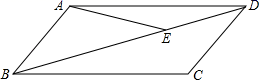
17. 如图，在▱ABCD中，点E是对角线BD上一点，且AB＝AE＝DE，若∠ABC＝51°．求∠DAE的度数．
18. 如图，已知平行四边形 的对角线 和 交于点O，且 ， ，求 的周长.
19. 如图是某区部分街道示意图，其中 垂直平分 .从 站乘车到 站只有两条路线有直接到达的公交车，路线1是 ，且长度为5公里，路线2是 ，求路线2的长度.
20. 如图，在 中， 于点E， 于点F，连接 ， ．求证： ．
21. 如图，在5×5的方格纸中，每个小正方形的边长均为1，A，B两点均在小正方形的顶点上，请按下列要求，在图1，图2中各画一个四边形（所画四边形的顶点均在小正方形的顶点上）
(1)、在图1中画四边形ABCD，使其为中心对称图形.(2)、在图2中画以A，B，E，F为顶点的平行四边形，且其中一条对角线长等于3.22. 如图，在 ABCD中，点E在边BC上，点F在边AD上，AF=CE，EF与对角线BD相交于点O。
(1)、求证：O是BD的中点。(2)、若EF⊥BD， ABCD的周长为24，连结BF，则△ABF的周长为 。23. 如图，在▱ABCD中，对角线AC，BD相交于点O，AB⊥AC，AB=3cm，BC=5cm.点P从A点出发沿AD方向匀速运动，速度为1cm/s，连接PO并延长交BC于点Q.设运动时间为t(s)(0<t<5)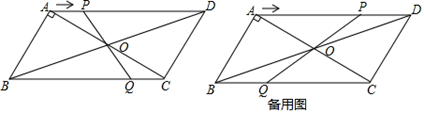
(1)、当t为何值时，四边形ABQP是平行四边形？(2)、当t=3时四边形OQCD的面积为多少？24. 如图，在四边形ABCD中，AB∥CD，∠BAD的平分线AE交CD于点F，交BC的延长线于点E，且AB＝BE.
(1)、求证：四边形ABCD是平行四边形；(2)、连结BF，若BF⊥AE，∠E＝60°，AB＝6，求四边形ABCD的面积.25. 如图1，在平面直角坐标系中，直线y= x+4与x轴、y轴分别交于点B，A。点P在线段OB上，且PB=m，点Q在直线AB上，Q的横坐标为m，连结PQ，以PQ，OQ作 PQOC。
(1)、当m=3时，求点C的坐标；(2)、若 PQOC的面积等于18，求m的值；(3)、如图2，作点P关于原点O的对称点M，以BM为直角边在x轴下方作Rt△BMN，使得∠MBN=30°，∠BMN=90°，当点C恰好落在△BMN的一边上时，求m的值。26. 阅读下面材料，并回答下列问题：小明遇到这样一个问题，如图，在 中， 分别交 于点 ，交 于点 .已知 ，求 的值.
小明发现，过点 作 ，交 的延长线于点 ，构造 ，经过推理和计算能够使问题得到解决（如图）
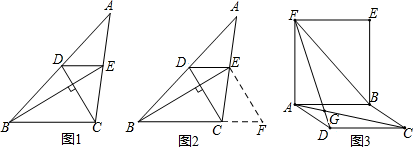
请你回答：
(1)、证明： ；(2)、求出 的值；(3)、参考小明思考问题的方法，解决问题；如图，已知 和矩形 与 交于点 .求 的度数.