初中数学苏科版八年级上册5.1 物体位置的确定同步练习

试卷更新日期：2021-06-21 类型：同步测试

进入出卷网下载

一、单选题

1. 下列叙述中，不能确定位置的是（）

A、小华在某会场的座位是5排8号 B、某城市位于东经108°，北纬39° C、A城与B城相距15 km D、船C在观测点A北偏东40°方向上30 km处

查看试题解析
2. 小李、小王、小张、小谢原有位置如图（横为排、竖为列），小李在第2排第4列，小王在第3排第3列，小张在第4排第2列，小谢在第5排第4列.撤走第一排，仍按照原有确定位置的方法确定新的位置，下列说法正确的是（）.

A、小李现在位置为第1排第2列 B、小张现在位置为第3排第2列 C、小王现在位置为第2排第2列 D、小谢现在位置为第4排第2列

查看试题解析
3. 下列说法错误的是（）

A、点 $(2, 3)$ 和点 $(3, 2)$ 表示同一个点 B、点 $(- 4, 1)$ 与点 $(4, - 1)$ 关于原点对称 C、坐标轴上的点的横坐标与纵坐标至少有一个为0 D、第一象限内的点的横坐标与纵坐标均为正数

查看试题解析
4. 根据下列表述，能确定位置的是（）

A、五一广场南区 B、岳麓山北偏东42º C、学校致诚厅5排9座 D、学校操场的西面

查看试题解析
5. 根据下列表述，能确定具体位置的是（）

A、实验中学东 B、南偏西30° C、东经120° D、会议室第7排，第5座

查看试题解析
6. 如果用有序数对（3，2）表示教室里第3列第2排的座位，则位于第5列第4排的座位应记作（）

A、（4，5） B、（5，4） C、（5，2） D、（4，5）

查看试题解析
7. 根据下列表述，能确定位置的是 $($ 　　 $)$

A、天益广场南区 B、凤凰山北偏东 $42^{\circ}$ C、红旗影院5排9座 D、学校操场的西面

查看试题解析
8. 如果从货船A测得小岛B在货船A的北偏东30°方向500米处，那么从小岛B看货船A的位置，此时货船A在小岛B的（）

A、南偏西30°方向500米处 B、南偏西60°方向500米处 C、南偏西30°方向 $250 \sqrt{3}$ 米处 D、南偏西60°方向 $250 \sqrt{3}$ 米处

查看试题解析
9. 下列五个命题：
①如果两个数的绝对值相等，那么这两个数的平方相等；②内错角相等；③在同一平面内，垂直于同一条直线的两条直线互相平行；④两个无理数的和一定是无理数；⑤坐标平面内的点与有序数对是一一对应的.其中真命题的个数是（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
10. 如果用有序数对（3，2）表示教室里第3列第2排的座位，则位于第5列第4排的座位应记作（　　）

A、（4，5） B、（5，4） C、（3，2） D、（2，3）

查看试题解析
11. 在某个电影院里，如果用（2，15）表示2排15号，那么5排9号可以表示为（　　）

A、（2，15） B、（2，5） C、（5，9） D、（9，5）

查看试题解析
12. 如图，将一等边三角形的三条边各8等分，按顺时针方向（图中箭头方向）标注各等分点的序号0、1、2、3、4、5、6、7、8，将不同边上的序号和为8的两点依次连接起来，这样就建立了“三角形”坐标系．在建立的“三角形”坐标系内，每一点的坐标用过这一点且平行（或重合）于原三角形三条边的直线与三边交点的序号来表示（水平方向开始，按顺时针方向），如点 $A$ 的坐标可表示为（1，2，5），点 $B$ 的坐标可表示为（4，1，3），按此方法，则点 $C$ 的坐标可表示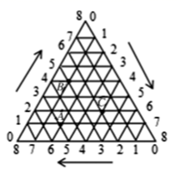为（）

A、 $(2 ， 6 ， 4)$ B、 $(6 ， 6 ， 4)$ C、 $(2 ， 4 ， 2)$ D、 $(4 ， 6 ， 6)$

查看试题解析
13. 满足等式 $| x | + 5 | y | = 10$ 的整数对 $(x, y)$ 共有（）

A、5对 B、6对 C、8对 D、10对

查看试题解析
14. 如图，雷达探测器测得六个目标A，B，C，D，E，F出现，按照规定的目标表示方法，目标E，F的位置表示为E(3，300°)，F(5，210°)，按照此方法在表示目标A，B，C，D的位置时，其中表示错误的是（）

A、A(4，30°) B、B(2，90°) C、C(6，120°) D、D(3，240°)

查看试题解析

二、填空题

15. 下列四个命题：①直角坐标系中的点与有序实数对一一对应；②若 $a$ 大于0， $b$ 不小于0，则点 $P (- a, - b)$ 在第三象限；③过一点有且只有一条直线与已知直线平行；④若 $y = \sqrt{- {(x - 1)}^{2}} + 4$ ，则 $\frac{x}{y}$ 的算术平方根是 $\frac{1}{2}$ .其中，是真命题的有.（写出所有真命题的序号）

查看试题解析
16. 若电影票上座位是12排5号可记为（12，5），则（5，6）表示．

查看试题解析
17. 如果将电影票上“6排3号”简记为（6，3），那么“10排9号”可表示为．

查看试题解析
18. 将正整数按如图的规律排列，若用有序数对（m，n）表示从上到下第m行，和该行从左到右第n个数，如（4，2）表示整数8，则（6，3）表示的整数是

查看试题解析
19. 如果把3排6号的电影票记作(3，6)，那么(5，7)表示的电影票号是．

查看试题解析
20. 如果座位表上“ $6$ 列 $3$ 行”记作 $(6, 3)$ ，那么 $(4, 3)$ 表示．

查看试题解析
21. 2019年，部分国家及经济体在全球的创新综合排名、创新产出排名和创新效率排名情况如图所示，某国创新综合排名全球第13，创新效率排名全球第．

查看试题解析
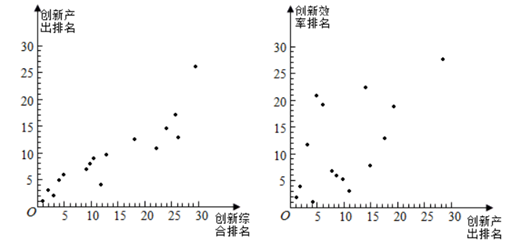22. 以学校所在的位置为原点，分别以向东、向北方向为x轴、y轴正方向．若出校门向东走100米，再向北走120米记作（100，120），小强家的位置是（-150，200）的含义是.

查看试题解析
23. 如果电影院的6排3号座位用（6，3）表示，那么该影院的7排5号座位可以表示为.

查看试题解析
24. 在某个电影院里，如果用(3，12)表示 3 排 12 号，那么 2 排 5 号可以表示为.

查看试题解析

三、解答题

25. 如图，用（-1，0）表示A点的位置，用（2，1）表示B点的位置，那么：

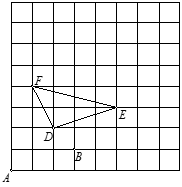(1)、画出直角坐标系。

(2)、写出△DEF的三个顶点的坐标。

(3)、在图中表示出点M（6，2），N（4，4）的位置。

查看试题解析

四、作图题

26. 下图中每个小方格的边长为1厘米。

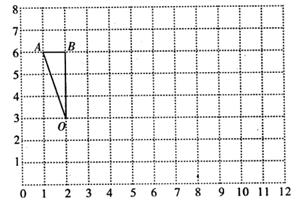(1)、用数对表示三角形的三个顶点，A( ， )，O( ， )，B( ， )。这个角形的面积是( )平方厘米。

(2)、将图中的三角形绕点O顺时针旋转90°，画出旋转后的图形。

(3)、将图中的三角形按2：1放大，画出放大后的三角形，放大后三角形的面积是平厘米。

(4)、如果把三角形ABO以BO为轴旋转一周，旋转后的图形的体积是立方米。

查看试题解析

五、综合题

27. 如图，一只甲虫在 $5 \times 5$ 的网格（每小格边长为1个单位长度）上沿着网格线运动．规定：向上和向右运动记为正，向左和向下运动记为负．如果甲虫从A到B记为 $A \to B (+ 1 ， + 4)$ ，从D到C记为 $D \to C (- 1 ， + 2)$ ，其中括号内前一个数字代表向左或向右的运动，后一个数字代表向上或向下的运动．

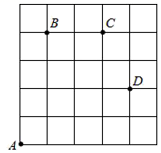(1)、从B到D记为 $B \to D$ （，）；

(2)、若这只甲虫的行走路线为 $A \to B \to C \to D$ ，则它行走的全路程长度为个单位长度：

(3)、甲虫从点B出发前往P点的位置，运动的路径按照 $(+ 1 ， - 3) ， (+ 2 ， + 2) ， (- 1 ， + 2)$ ，请在图中标出点P的位置．

查看试题解析
28. 随着科学技术的发展，物流快递已经可以由机器人派送了。机器人能按照设计的指令完成各种动作.在坐标平面上，根据指令{s，a}（s≥0， $0^{\circ} < a < 180^{\circ}$ ）机器人能完成下列动作：先原地逆时针旋转角度a，再朝其对面方向沿直线行走距离s.

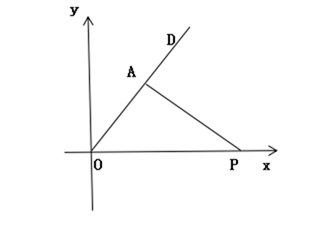(1)、填空：如图，若机器人在直角坐标系的原点，且面对y轴的正方向，现要使其移动到点A（2，2），则给机器人发出的指令应是（无需过程）；

(2)、机器人在完成上述指令后，发现在P（ $2 \sqrt{3} + 2 ， 0$ ）处有一小球正向坐标原点做匀速直线运动，已知小球滚动的速度与机器人行走的速度相同，若忽略机器人原地旋转的时间，请你给机器人发一个指令，使它能刚好截住小球.[第二小题写解题过程]

查看试题解析
29. 在边长为1的小正方形组成的网格中，把一个点先沿水平方向平移 $| a |$ 格（当 $a$ 为正数时，表示向右平移．当 $a$ 为负数时，表示向左平移），再沿竖直方向平移 $| b |$ 格（当 $b$ 为正数时，表示向上平移．当 $b$ 为负数时，表示向下平移），得到一个新的点，我们把这个过程记为 $(a ， b)$ ．例如，从 $A$ 到 $B$ 记为： $A \to B (+ 1 ， + 3)$ ．从 $C$ 到 $D$ 记为： $C \to D (+ 1 ， - 2)$ ，回答下列问题：

(1)、如图1，若点 $A$ 的运动路线为： $A \to B \to C \to A$ ，请计算点 $A$ 运动过的总路程．

(2)、若点 $A$ 运动的路线依次为： $A \to M (+ 2 ， + 3)$ ， $M \to N (+ 1 ， - 1)$ ， $N \to P (- 2 ， + 2)$ ， $P \to Q (+ 4 ， - 4)$ ．请你依次在图2上标出点 $M$ 、 $N$ 、 $P$ 、 $Q$ 的位置．

(3)、在图 $2$ 中，若点 $A$ 经过 $(m ， n)$ 得到点 $E$ ，点 $E$ 再经过 $(p ， q)$ 后得到 $Q$ ，则 $m$ 与 $p$ 满足的数量关系是． $n$ 与 $q$ 满足的数量关系是．

查看试题解析
30. 如图，蚂蚁在5×5的方格(每个小方格的边长均为1 cm)上沿着网格线运动．它从A处出发去寻找B，C，D处的伙伴，规定：向上向右走为正，向下向左走为负．如果从A到B记为：A→B(＋1，＋4)，从B到A记为：B→A(－1，－4)，其中第一个数表示左右方向，第二个数表示上下方向，那么图中：

(1)、A→D( ， )；D→B( ， )；C→B( ， )．

(2)、若蚂蚁的行走路线为A→B→C→D，请计算蚂蚁走过的路程．

(3)、若蚂蚁从A处出发去寻找伙伴，它的行走路线依次为(＋1，＋2)，(＋3，－1)，(－2，＋2)，请在图中标出这只蚂蚁伙伴的位置E.

(4)、在(3)中，若蚂蚁每走1 cm需要消耗1.5焦耳的能量，则蚂蚁在寻找伙伴E的过程中总共需要消耗多少焦耳的能量？

查看试题解析
31. 阅读：一动点沿着数轴向右平移3个单位，再向左平移2个单位，相当于向右平移1个单位，用实数加法表示为3+(-2)=1．若坐标平面上的点作如下平移：沿x轴方向平移的数量为a（向右为正，向左为负，平移 $| a |$ 个单位），沿y轴方向平移的数量为b（向上为正，向下为负，平移 $| b |$ 个单位），则把有序数对{a，b}叫做这一平移的“平移量”；“平移量”{a，b}与“平移量”{c，d}的加法运算法则为{a，b}+{c，d}={a+c，b+d}．解决问题：

(1)、计算： ${3 ， 1} + {1 ， 2}$ ，

(2)、动点P从坐标原点O出发，先按照“平移量”{3，1}平移到A，再按照“平移量”{1，2}平移到B；若先把动点P按照“平移量”{1，2}平移到C．再按照“平移量”{3，1}平移，最后的位置还是点B．请你在图1中画出四边形OABC；

(3)、如图2，一艘船从码头O出发，先航行到湖心岛码头P(2，3)，再从码头P航行到码头Q(5，5)，最后回到出发点O．请用“平移量”加法算式表示它的航行过程．

查看试题解析
32. 如图，图中显示了10名同学平均每周用于阅读课外书的时间和用于看电视的时间（单位： $h$ ）

(1)、用有序实数对表示图中各点；

(2)、平均每周用于阅读课外书的时间和用于看电视的时间的总共 $10h$ 的同学有多少名？

(3)、如果设平均每周用于阅读课外书的时间超过用于看电视的时间的同学为 $a$ 名，设平均每周用于阅读课外书的时间少于用于看电视的时间的同学为 $b$ 名，求 $b - a$ 的值．

查看试题解析
33. 如图，一只甲虫在 $5 \times 5$ 的方格（每小格边长为1）上沿着网格线运动，他从 $A$ 处出发去看望 $B$ 、 $C$ 、 $D$ 处的其他甲虫，规定：向上向右走均为正，向下向左走均为负，如果从 $A$ 到 $B$ 记为 $A \to B {1 ， 4}$ ，从 $B$ 到 $A$ 记为： $B \to A {- 1 ， - 4}$ ，其中第一个数表示左右方向，第二个数表示上下方向.

(1)、图中 $A \to C$ { ， }， $C \to B$ { ， }；

(2)、若这只甲虫的行走路线为 $A \to B \to C \to D$ ，请计算该甲虫走过的最短路程.

(3)、若图中另有两个格点 $M$ 、 $N$ ，且 $M \to A {3 - a ， b - 4}$ ， $M \to N {5 - a ， b - 2}$ ，则 $N \to A$ 应记为什么？直接写出你的答案.

查看试题解析
34. 观察下列两个等式： $2 - \frac{1}{3} = 2 \times \frac{1}{3} + 1$ ， $5 - \frac{2}{3} = 5 \times \frac{2}{3} + 1$ ．给出定义如下：使等式 $a - b = a b + 1$ 成立的一对有理数 $a$ ， $b$ 为“共生有理数对”，记为 $(a ， b)$ ．如：数对 $(2 ， \frac{1}{3})$ ， $(5 ， \frac{2}{3})$ 都有“共生有理数对”．

(1)、数对 $(- 2 ， 1)$ ， $(3 ， \frac{1}{2})$ 中是“共生有理数对”的是．

(2)、请再写出另外一对符合条件的“共生有理数对”（不能与题目中已有的重复）．

(3)、小丁说：“若 $(a ， b)$ 是‘共生有理数对’，则 $(- b ， - a)$ 一定是‘共生有理数对’．”请你用（2）中写出的“共生有理数对”验证小丁的说法．

查看试题解析
35. 一般情况下， $\frac{b}{a} + \frac{1}{b} = \frac{3}{a b} + 1$ 不成立，但有些数可以使得它成立，例如：a＝1，b＝2．我们称使得 $\frac{b}{a} + \frac{1}{b} = \frac{3}{a b} + 1$ 成立的一对数a ， b为“相伴数对”，记为（a ， b）．

(1)、判断数对（﹣2，1），（3，3）是否是“相伴数对”；

(2)、若（k ， ﹣1）是“相伴数对”，求k的值；

(3)、若（4，m）是“相伴数对”，求代数式 $\frac{4 m - [3 m^{2} - 2 (4 m - 1)]}{3 m (m - 4)}$ 的值．

查看试题解析
36. 某城市大剧院地面的一部分为扇形，观众席的座位按下列方式置：

排数

1

2

3

4

…

座位数

50

53

56

59

…

按这种方式排下去．

(1)、第5，6排各有多少个座位；

(2)、第n排有多少个座位？

(3)、在(2)的代数式中，当n为28时，有多少个座位？

查看试题解析

排数	1	2	3	4	…
座位数	50	53	56	59	…

初中数学苏科版八年级上册5.1 物体位置的确定 同步练习

一、单选题

二、填空题

三、解答题

四、作图题

五、综合题

初中数学苏科版八年级上册5.1 物体位置的确定同步练习