初中数学苏科版八年级上册第四章实数单元测卷

试卷更新日期：2021-06-21 类型：单元试卷

进入出卷网下载

一、单选题

1. 下列命题： (1) $\sqrt[3]{a^{3}}$ ＝a，(2) $\sqrt{a^{2}}$ ＝a，(3)无限小数都是无理数，(4)有限小数都是有理数，(5)实数分为正实数和负实数两类.正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列等式正确的是（）

A、 $\sqrt{\frac{49}{144}} = \pm \frac{7}{12}$ B、 $- \sqrt[3]{- \frac{27}{8}} = - \frac{3}{2}$ C、 $\sqrt{- 9} = - 3$ D、 $\sqrt[3]{{(- 8)}^{2}} = 4$

查看试题解析
3. 在下列结论中，正确的是（）

A、 $\sqrt{{(- \frac{5}{4})}^{2}} = \pm \frac{5}{4}$ B、x²的算术平方根是x C、﹣x²一定没有平方根 D、 $\sqrt{9}$ 的平方根是 $\pm \sqrt{3}$

查看试题解析
4. 下列说法正确的是（）

A、144的平方根等于12 B、25的算术平方根等于5 C、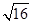的平方根等于±4 D、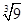等于±3

查看试题解析
5. 下列说法正确的是（）

A、1的平方根是1 B、－8的立方根是－2 C、 $\sqrt{4} = \pm 2$ D、 $\sqrt{{(- 2)}^{2}} = - 2$

查看试题解析
6. 下列说法正确的是（）

A、（﹣3）²的平方根是3 B、 $\sqrt{16}$ ＝±4 C、1的平方根是1 D、4的算术平方根是2

查看试题解析
7. 下列运算正确的是（）

A、 $\sqrt{{(-2)}^{2}}$ =2 B、 $\sqrt{{(-2)}^{2}}$ =﹣2 C、 $\sqrt{4}$ =±2 D、 $\sqrt[3]{8}$ =±2

查看试题解析
8. 小飞测量身高近似1.71米，若小飞的身高记为x，则他的实际身高范围为（）

A、1.7≤x≤1.8 B、1.705＜x＜1.715 C、1.705≤x＜1.715 D、1.705≤x≤1.715

查看试题解析

二、填空题

9. 如果一个正数的两个平方根分别为2m+1和2-m，则这个数是.

查看试题解析
10. 已知：一个正数的两个平方根分别是2a－2和a－4，则这个正数的立方根是.

查看试题解析
11. 一个正数的两个平方根为a+2和a-6，则这个数为.

查看试题解析
12. 一个正数的两个平方根分别是2m－1和4－3m，则m=.

查看试题解析
13. 若某个正数的两个平方根分别是2a﹣1与2a+5，则a=.

查看试题解析
14. 地球的半径约为6.4×10⁶m，这个近似数精确到m.

查看试题解析

三、计算题

15. 求下列各式中 $x$ 的值：

(1)、 ${(x + 1)}^{2} = 4$ ；

(2)、 $8 x^{3} = 27$ .

查看试题解析
16. 求式中x的值：

(1)、 $x^{2} - 36 = 0$

(2)、 ${(x - 2)}^{3} + 29 = 2$ .

查看试题解析
17. 计算：

(1)、 $2021^{0} - \sqrt{4}$

(2)、 $| \sqrt{3} - 2 | + \sqrt[3]{- 8}$

查看试题解析
18. 求下列各式中的 $x$ 的值：

(1)、 $4 x^{2} - 9 = 0$

(2)、 ${(x - 1)}^{3} = 64$

查看试题解析
19. 计算：

(1)、 $\sqrt{36} - \sqrt[3]{27} + {(\sqrt{2})}^{2}$

(2)、 ${(- \sqrt{6})}^{2} - \sqrt{9} - \sqrt[3]{8}$

查看试题解析
20.

(1)、计算： $\sqrt{4} - \sqrt[3]{- 27} + | - π |$

(2)、解方程： $8 {(x + 1)}^{3} = 27$

查看试题解析

四、解答题

21. 阅读下列材料：“为什么 $\sqrt{2}$ 不是有理数”．
假 $\sqrt{2}$ 是有理数，那么存在两个互质的正整数m，n，使得 $\sqrt{2}$ = $\frac{n}{m}$ ，于是有2m²=n² ．
∵2m²是偶数，∴n²也是偶数，∴n是偶数．
设n=2t（t是正整数），则n²=2m，∴m也是偶数
∴m，n都是偶数，不互质，与假设矛盾．
∴假设错误
∵ $\sqrt{2}$ 不是有理数
有类似的方法，请证明 $\sqrt{3}$ 不是有理数．

查看试题解析
22. 阅读下面材料：随着人们认识的不断深入，毕达哥拉斯学派逐渐承认 $\sqrt{2}$ 不是有理数，并给出了证明．假设是 $\sqrt{2}$ 有理数，那么存在两个互质的正整数p，q，使得 $\sqrt{2}$ = $\frac{p}{q}$ ，于是p= $\sqrt{2}$ q，两边平方得p²=2q² ．因为2q²是偶数，所以p²是偶数，而只有偶数的平方才是偶数，所以p也是偶数．因此可设p=2s，代入上式，得4s²=2q² ，即q²=2s² ，所以q也是偶数，这样，p和q都是偶数，不互质，这与假设p，q互质矛盾，这个矛盾说明， $\sqrt{2}$ 不能写成分数的形式，即 $\sqrt{2}$ 不是有理数．
请你有类似的方法，证明 $\sqrt[3]{2}$ 不是有理数．

查看试题解析
23. 若 $x + y$ 是9的算术平方根， $x - y$ 的立方根是 $- 2$ ，求 $x^{2} - y^{2}$ 的值.

查看试题解析
24. 已知x＋1的平方根为±3，y－1的立方根为3，求x＋y的平方根.

查看试题解析
25. 已知2a-1的平方根为±3，2a+b-1的立方根为2，求a+2b的平方根

查看试题解析
26. 已知a+7的立方根是2，一个正数b的平方根分别是5x﹣2和4﹣6x，求3b+4a的平方根.

查看试题解析
27. 若3是 $2 x - 1$ 的平方根， $- 2$ 是 $y - 3 x$ 的立方根，求 $3 x + y$ 的平方根.

查看试题解析
28. 已知x-2的算术平方根为2，2x+y+4的立方根是2，求 $x^{2} + y^{2}$ 的平方根.

查看试题解析
29. 已知5a－1的平方根是±3，4a+2b＋1的平方根是±1，求4a－2b的平方根.

查看试题解析
30. 已知2a－1的算术平方根为3，3a+b－1的算术平方根为4，求a+2b的平方根.

查看试题解析
31. 已知 $2 a - 1$ 的算术平方根是 $3$ ， $3 a + b - 1$ 的立方根是 $2$ ，求 $a - 2 b$ 的平方根.

查看试题解析
32. 观察被开方数a的小数点与算术平方根 $\sqrt{a}$ 的小数点的移动规律:

a

0.0001

0.01

1

100

10000

$\sqrt{a}$

0.01

x

1

y

100

(1)、填空:x= ， y=.

(2)、根据你发现的规律填空:
①已知 $\sqrt{2}$ ≈1.414，则 $\sqrt{200}$ = ， $\sqrt{0.02}$ =；

② $\sqrt{m}$ = 0.274，记 $\sqrt{10000 m}$ 的整数部分为x,则 $\sqrt[3]{\frac{1}{x}}$ =.

查看试题解析

a	0.0001	0.01	1	100	10000
$\sqrt{a}$	0.01	x	1	y	100

初中数学苏科版八年级上册第四章 实数 单元测卷

一、单选题

二、填空题

三、计算题

四、解答题

初中数学苏科版八年级上册第四章实数单元测卷