初中数学苏科版八年级上册4.3, 4.4实数及近似数 同步练习
试卷更新日期:2021-06-21 类型:同步测试
一、单选题
-
1. 用四舍五入法,865600精确到千位的近似值是( )A、 B、 C、 D、8650002. 今年10月环太湖中长跑中参赛选手达到21780人,这个数精确到千位表示约为( )A、2.2×104 B、22000 C、2.1×104 D、223. 实数 在数轴上表示的位置如图所示,则( )
 A、 B、 C、 D、4. 如图,是小明同学在数轴上标注了这组数中 的两个无理数的位置,则这组数从小到大排列正确的是( )
A、 B、 C、 D、4. 如图,是小明同学在数轴上标注了这组数中 的两个无理数的位置,则这组数从小到大排列正确的是( )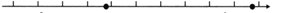 A、 B、 C、 D、5. 如图,数轴上表示1, 的点分别为A和B,若A为BC的中点,则点C表示的数是( )
A、 B、 C、 D、5. 如图,数轴上表示1, 的点分别为A和B,若A为BC的中点,则点C表示的数是( )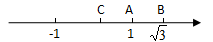 A、 -1 B、1- C、 -2 D、2-6. 实数a,b在数轴上的位置如图所示,下列结论错误的是( )
A、 -1 B、1- C、 -2 D、2-6. 实数a,b在数轴上的位置如图所示,下列结论错误的是( ) A、|a|<1<|b| B、1<–a<b C、1<|a|<b D、–b<a<–17. 某种鲸的体重约为 ,关于这个近似数,下列说法正确的是( )A、精确到百分位 B、精确到0.01 C、精确到千分位 D、精确到千位8. 下列选项中,与数轴上的点一一对应的是( )A、实数 B、有理数 C、正整数和0 D、无理数9. 下列说法正确的是( )A、-6和-4之间的数都是有理数 B、数轴上表示 的点一定在原点的左边 C、在数轴上离开原点的距离越远的点表示的数越大 D、-1和0之间有无数个负数10. 下列个数中,小于-2的数是( )
A、|a|<1<|b| B、1<–a<b C、1<|a|<b D、–b<a<–17. 某种鲸的体重约为 ,关于这个近似数,下列说法正确的是( )A、精确到百分位 B、精确到0.01 C、精确到千分位 D、精确到千位8. 下列选项中,与数轴上的点一一对应的是( )A、实数 B、有理数 C、正整数和0 D、无理数9. 下列说法正确的是( )A、-6和-4之间的数都是有理数 B、数轴上表示 的点一定在原点的左边 C、在数轴上离开原点的距离越远的点表示的数越大 D、-1和0之间有无数个负数10. 下列个数中,小于-2的数是( )
A、- B、- C、- D、-111. 下列说法正确的是 ( )A、近似数5000万精确到个位 B、近似数4.60精确到十分位 C、近似数4.31万精确到0.01 D、 1.45 104精确到百位
12. 由四舍五入法得到的近似数8.30万,它是精确到( )位.A、精确到百分位 B、精确到百位 C、精确到千位 D、精确到万位13. 3.0269精确到百分位的近似值是( )A、 3.026 B、3.027 C、3.02 D、3.0314. 如图,在Rt△OBC中,OC=1,OB=2,数轴上点A所表示的数为a,则a的值是( )
104精确到百位
12. 由四舍五入法得到的近似数8.30万,它是精确到( )位.A、精确到百分位 B、精确到百位 C、精确到千位 D、精确到万位13. 3.0269精确到百分位的近似值是( )A、 3.026 B、3.027 C、3.02 D、3.0314. 如图,在Rt△OBC中,OC=1,OB=2,数轴上点A所表示的数为a,则a的值是( )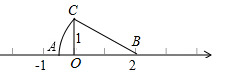 A、-
A、-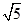 -2
B、-
-2
B、- 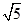 C、
C、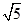 ﹣2
D、﹣
﹣2
D、﹣ 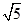 +2
15. 有下列说法:①有理数和数轴上的点一一对应;②不带根号的数一定是有理数;③负数没有立方根;④ 是17的平方根。其中正确的有( )
+2
15. 有下列说法:①有理数和数轴上的点一一对应;②不带根号的数一定是有理数;③负数没有立方根;④ 是17的平方根。其中正确的有( )
A、0个 B、1个 C、2个 D、3个二、填空题
-
16. 比较大小: (填“>”、“=”或“<”).17. 已知地球的半径约为6.4×103km,这个近似数精确度为km.18. 比较大小: (填“>”或“<”=).19. 下列实数:12,- ,|﹣1|, ,0.1010010001…, , 中,有理数有个.20. 比较大小: (填>或<或=).21. 某人一天饮水1890mL,用四舍五入法对1890mL精确到100mL表示为.22. 近似数13.7万精确到位.23. 近似数40.66精确到位.24. 某人一天饮水1890毫升,将1890精确到1000后可以表示为.25. 比较大小: 2.26. 计算: + =.27. 如图,在数轴上,过数2表示的点B作数轴的垂线,以点B为圆心1为半径画弧,交其垂线于点A,再以原点O为圆心,OA长为半径画弧,交数轴于点C,则点C表示的数为.
 28. 有一个数值转换器,原理如下:
28. 有一个数值转换器,原理如下:
当输入的x = 4时,输出的y等于 .
29. 如图,正方形 的边 落在数轴上,点 表示的数为 ,点 表示的数为 ,以 点为圆心, 长为半径作圆弧与数轴交于点 ,则点 表示的数为.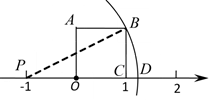 30. 数2.185 精确到位.
30. 数2.185 精确到位.三、解答题
-
31. (1)计算:|﹣3|+(π+1)0﹣;
(2)已知:(x+1)2=16,求x.
32. 化简:|﹣|﹣|3﹣|.33.求出下列各数的相反数,在数轴上表示下列各数以及它们的相反数,并用“<”连接:﹣ , , 0, .
 34.
34.在数轴上点A表示的数是 .
(1)若把点A向左平移2个单位得到点为B,则点B表示的数是什么?
(2)点C和(1)中的点B所表示的数互为相反数,点C表示的数是什么?
(3)求出线段OA,OB,OC的长度之和.
 35. 计算:36. 计算:37.
35. 计算:36. 计算:37.如图所示,数轴上表示1和对应点分别为A、B,点B到点A的距离等于点C到点O的距离相等,设点C表示的数为x.
(1)请你写出数x的值;
(2)求(x﹣)2的立方根.
 38.
38.已知实数a、b、c在数轴上的位置如图所示,化简:﹣|a+b|++|b﹣c|
 39. 问:你能比较两个数20082009和20092008的大小吗?
39. 问:你能比较两个数20082009和20092008的大小吗?为了解决这个问题,我们先把它抽象成数学问题,写出它的一般形式,比较nn+1与(n+1)n的大小(n为正整数),从分析n=1,n=2,n=3…的情形入手,通过归纳,发现规律,猜想出结论.
(1)比较各组数的大小①12和21;②23和32;③34和43;④45和54
(2)由(1)猜想出nn+1与(n+1)n的大小关系是?
(3)由(2)可知:20082009与 20092008。的大小
四、综合题
-
40. 我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果ax+b=0,其中a、b为有理数,x为无理数,那么a=0且b=0.
运用上述知识,解决下列问题:
(1)、如果(a+2) -b+3=0,其中a、b为有理数,那么a= , b=;
(2)、如果2b-a-(a+b-4) =5,其中a、b为有理数,求3a+2b的平方根.