初中数学浙教版七年级下学期期末复习专题14 分式方程及其应用

试卷更新日期：2021-06-21 类型：复习试卷

进入出卷网下载

一、单选题

1. 把方程 $3 x + \frac{2 x - 1}{3} = 3 - \frac{x + 1}{2}$ 去分母正确的是（）

A、 $18 x + 2 (2 x - 1) = 18 - 3 (x + 1)$ B、 $3 x + (2 x - 1) = 3 - (x + 1)$ C、 $18 x + (2 x - 1) = 18 - (x + 1)$ D、 $3 x + 2 (2 x - 1) = 3 - 3 (x + 1)$

查看试题解析
2. 下列关于x的方程： $\frac{1}{x} + x = 1, \frac{x}{3} + \frac{3 x}{4} = \frac{2}{5}, \frac{1}{x - 1} = \frac{4}{x}, \frac{x^{2} - 1}{x + 1} = 2$ 中，分式方程的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 用换元法解分式方程 $\frac{x}{x^{2} + 1} - \frac{{(x + 1)}^{2}}{x} + 1 = 0$ 时，如果设 $\frac{x}{x^{2} + 1} = y$ ，那么原方程可以变形为整式方程（）

A、 $y^{2} - 3 y - 1 = 0$ B、 $y^{2} + 3 y - 1 = 0$ C、 $y^{2} - y - 1 = 0$ D、 $y^{2} + y - 1 = 0$

查看试题解析
4. 把方程 $\frac{x - 1}{0.6} + \frac{0.5 x + 8}{0.9} = 12$ 的分母化为整数，结果应为（）

A、 $\frac{x - 1}{6} + \frac{5 x + 8}{9} = 12$ B、 $\frac{10 x - 10}{6} + \frac{5 x + 80}{9} = 12$ C、 $\frac{10 x - 10}{6} + \frac{5 x + 80}{9} = 120$ D、 $\frac{x - 1}{6} + \frac{5 x + 8}{9} = 120$

查看试题解析
5. 使分式 $\frac{x}{x - 3}$ 和分式 $\frac{x + 1}{x - 1}$ 相等的 $x$ 值是（）

A、-5 B、-4 C、-3 D、-1

查看试题解析
6. 若关于 $x$ 的分式方程 $\frac{2}{x - 3} + \frac{x + m}{3 - x} = 2$ 有增根，则 $m$ 的值是（）．

A、 $m = - 1$ B、 $m = 0$ C、 $m = 3$ D、 $m = 0$ 或 $m = 3$

查看试题解析
7. 崇左市即将跨入高铁时代，南宁至凭祥的高速铁路正在建设中，甲工程队每天比乙工程队多修建20 m，甲工程队修建6000 m用的时间与乙工程队修建4800m用的时间一样.设乙工程队每天修建x m，则根据题意所列的方程是（）

A、 $\frac{6000}{x} = \frac{4800}{x + 20}$ B、 $\frac{6000}{x + 20} = \frac{4800}{x}$ C、 $\frac{6000}{x} = \frac{4800}{x} + 20$ D、 $\frac{6000}{x} = \frac{4800}{x - 20}$

查看试题解析
8. 已知关于x的分式方程 $\frac{x + m}{x - 3}$ ﹣1＝ $\frac{1}{x}$ 无解，则m的值是（）

A、﹣2或﹣3 B、0或3 C、﹣3或3 D、﹣3或0

查看试题解析
9. $x = - 1$ 是下列哪个分式方程的解（）

A、 $\frac{2}{x + 1} = \frac{1}{x}$ B、 $\frac{x + 1}{x^{2} - 1} = 0$ C、 $\frac{2}{x + 1} - \frac{1}{x + 2} = 0$ D、 $\frac{2}{x - 1} + \frac{1}{x + 2} = 0$

查看试题解析
10. 商家常将单价不同的A，B两种糖混合成“什锦糖”出售，记“什锦糖”的单价为：A，B两种糖的总价与A，B两种糖的总质量的比．现有两种“什锦糖”：一种是由相同千克数的A种糖和B种糖混合而成的“什锦糖”甲，另一种是由相同金额数的A种糖和B种糖混合而成的“什锦糖”乙．若B种糖比A种糖的单价贵40元/千克，“什锦糖”甲比“什锦糖”乙的单价贵5元/千克，则A种糖的单价为（）

A、50元/千克 B、60元/千克 C、70元/千克 D、80元/千克

查看试题解析

二、填空题

11. 方程 $\frac{x^{2}}{x + 3} = \frac{9}{x + 3}$ 的根是．

查看试题解析
12. 分式方程 $\frac{x}{x - 3} + 1 = \frac{m - 1}{x - 3}$ 有增根，则 $m =$

查看试题解析
13. 甲和乙同时从A地出发，匀速行走到B地．甲走完一半路程时，乙才走了4千米．乙走完一半路程时，甲已走了9千米．当甲走完全程时，乙未走完的路程还有千米

查看试题解析
14. 方程： $\frac{2}{x - 2} - \frac{k x}{x^{2} - 4} = \frac{3}{x + 2}$ 无解，则k的值为．

查看试题解析
15. 当x=时，分式 $\frac{3}{x}$ 与 $\frac{3}{x - 6}$ 互为相反数.

查看试题解析
16. 要在规定的日期内加工一批机器件,如果甲单独做,刚好在规定日期内完成,乙单独做则要超过3天.现在甲乙两人合作2天后,再由乙单独做,正好按期完成.则规定日期是天

查看试题解析

三、解答题

17. 解分式方程： $\frac{x + 2}{x - 2} - \frac{16}{x^{2} - 4} = \frac{1}{x + 2}$ ．

查看试题解析
18. 解下列方程（组）：

(1)、 $\frac{3}{x - 1} = \frac{2}{x}$

(2)、 ${\begin{array}{l} x - 2 y = 1 \\ 3 x - 4 (x - 2 y) = 5 \end{array}$

查看试题解析
19. 801班原有卫生区260平方米，现在由于某种原因变成了200平方米，因在打扫卫生时每分钟比原来少打扫15平方米，结果现在完成卫生任务的时间与原来的一样.
求：

(1)、原来每分钟打扫卫生多少平方米？

(2)、现在完成卫生任务要多少时间？

查看试题解析
20. 某社区积极响应正在开展的“文明城市创建工作”，组织甲、乙两个志愿工程队对社区的一些区域进行绿化改造.已知甲工程队每小时能完成的绿化面积是乙工程队每小时能完成的绿化面积的2倍，并且甲工程队完成300m²的绿化面积比乙工程队完成200m²的绿化面积少用2h.求乙工程队每小时能完成多少平方米的绿化面积？

查看试题解析
21. 已知 $(a + b) x^{2} - x^{\frac{1}{2} a + 2}$ +5=0是关于x的一元一次方程．

(1)、求a、b的值；

(2)、若y=a是关于y的方程 $\frac{y + 2}{6} - \frac{y - 1}{2} = (y - 3) - \frac{y - m}{3}$ 的解，求|a-b|-|b-m|的值．

查看试题解析
22. 以下是圆圆解方程 $\frac{x + 1}{2} - \frac{x - 3}{3}$ ＝1的解答过程．
解：去分母，得3（x+1）﹣2（x﹣3）＝1．

去括号，得3x+1﹣2x+3＝1．

移项，合并同类项，得x＝﹣3．

圆圆的解答过程是否有不符合题意？如果有不符合题意，写出正确的解答过程．

查看试题解析
23. 2020年由于新冠肺炎爆发，为预防疫情专家提出了“勤洗手，戴口罩” 的措施，口罩在市场上供不应求，生产口罩的主要材料是熔喷布。已知1吨熔喷布可以生产105万只医用一次性口罩，或者60万只KN95口罩。某生产熔喷布的企业要求在规定时间内完成100吨熔喷布的订单，为提高产量，现对生产车间进行改造，改造后每天比改造前多生产4吨熔喷布，结果在规定时间内多生产了40吨熔喷布。

(1)、现有一批熔喷布，若全部用来生产医用一次性口罩则可以生产420万只，则这批熔喷布全部用来生产KN95口罩则可以生产万只；

(2)、求该企业改造后熔喷布的日产量和企业要求规定的天数。

查看试题解析
24. 湖州奥体中心是一座多功能的体育场，目前体育场内有一块长80m，宽60m的长方形空地，体育局希望将其改建成花园小广场，设计方案如图，阴影区域是面积为192平方米的绿化区（四块相同的直角三角形），空白区域为活动区，且四周出口宽度一样.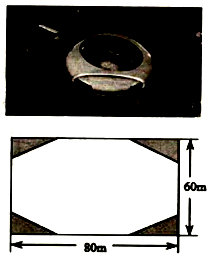

(1)、体育局先对四个绿化区域进行绿化，在完成工作量的 $\frac{1}{3}$ 后，施工方进行了技术改进，每天的绿化面积是原计划的两倍，结果提前四天完成四个绿化区域的改造，问原计划每天绿化多少平方米？

(2)、老师提出了一个问题：你能不能求出活动区的出口宽度是多少呢？

请你根据小丽的方法求出活动区的出口宽度，并把过程写下来.

查看试题解析