初中数学苏科版八年级上册3.2勾股定理逆定理 同步练习
试卷更新日期：2021-06-21 类型：同步测试
一、单选题
-
1. 下列长度的三条线段能组成直角三角形的是（ ）A、2， 3， 4 B、4，6，7 C、3，4， 5 D、6，8，112. 下列各组线段 、 、 中不能组成直角三角形的是（ ）A、 ， ， B、 ， ， C、 ， ， D、 ， ，3. 下列各组数中，能作为直角三角形三边长的是（ ）A、1，2，3 B、4，5，6 C、6，8，10 D、7，8，94. 下列由线段a、b、c组成的三角形是直角三角形的是（ ）A、a＝1， b＝2， c＝3； B、a＝4 ， b＝5 ，c＝6； C、a＝9， b＝12，c＝15； D、a＝13， b＝14 ，c＝155. 下列各组数不能作为直角三角形边长的是（ ）A、3，4，5 B、8，15，17 C、7，9，11 D、9，12，156. 分别以下列四组数为一个三角形的边长：（1）6，8，10，；（2）5，12，13；（3）8，15，17； （4）4，5，6，其中能构成直角三角形的有 （ ）A、4组 B、3组 C、2组 D、1组7. 在下列各组数据中，不能作为直角三角形的三边的是 （ ）A、3，4，6 B、7，24，25 C、6，8，10 D、9，12，158. 已知△ABC中，a、b、c分别是∠A，∠B，∠C的对边，下列条件不能判断△ABC是直角三角形的是 （ ）A、∠A＝∠C－∠B B、a2＝b2－c2 C、a：b：c＝2：3：4 D、 a＝
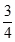，b＝ 
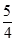，c＝1
9. 下列条件中，不能判断△ABC为直角三角形的是（ ）A、a=1.5，b=2，c=2.5 B、a：b：c=3：4：5 C、∠A+∠B=∠C D、∠A：∠B：∠C=3：4：510.一艘轮船和一艘渔船同时沿各自的航向从港口O出发，如图所示，轮船从港口O沿北偏西20°的方向行60海里到达点M处，同一时刻渔船已航行到与港口O相距80海里的点N处，若M、N两点相距100海里，则∠NOF的度数为（ ）
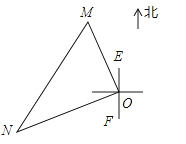A、50° B、60° C、70° D、80°二、填空题
-
11. 在△ABC中，若 AB＝2.5，AC＝2，当 BC＝时，∠C为直角。12. 一个三角形的三边之比为 ，且周长为60cm，则它的面积是 .
13.2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽弦图它是由四全等的直角三角形与中间的一个小正方形拼成的一个大正方形，如图所示，如果大正方形 的面积是13，小正方形的面积是1，直角三角形的短直角边为a，较长直角边为b，下列说法：
①a2+b2=13；②b2=1；③a2﹣b2=12；④ab=6．
其中正确结论序号是
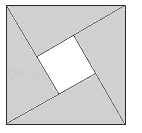14.如图，它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形．如果大正方形的面积是13，小正方形的面积是1，直角三角形的较短的直角边长为a，较长的直角边长为b，那么（a+b）2的值为
15. 在△ABC中，若三边长分别为9，12，15，则以两个这样的三角形拼成的长方形的面积为 ．
16. 有一个三角形的两边长是4和5，要使这个三角形成为直角三角形，则第三边长为17. 四边形ABCD中，AD=3，AB=4，BC=12，CD=13，∠BAD=90°，则△BDC为三角形．
18.如图，在2×2的正方形网格中有9个格点，已经取定点A和B，在余下的7个点中任取一点C，使△ABC为直角三角形的点C有 个．
19. 已知三角形三边的长分别为15、20、25，则这个三角形的形状是 ．
20. 三角形的三边分别为a，b，c，且（a﹣b）2+（a2+b2﹣c2）2=0，则三角形的形状为 ．
21. 有一根长24cm的小木棒，把它分成三段，组成一个直角三角形，且每段的长度都是偶数，则三段小木棒的长度分别是 cm，cm， cm．22. 三角形的三边长为a、b、c，且满足等式（a+b）2﹣c2=2ab，则此三角形是三角形（直角、锐角、钝角）．
23. 若△ABC的三边长分别为x+1，x+2，x+3，要使此三角形成为直角三角形，则x= ．
24. 在△ABC中，AB=7，BC=24，AC=25，则△ABC的面积是 ．
三、解答题
-
25. 在△ABC中， ，试判断△ABC的形状，并说明理由。
26. 一个三角形三边长的比为3：4：5，它的周长为60，求这个三角形的面积。27. 已知△ABC的三边分别为k2－1，2k，k2+1（k＞1），求证：△ABC是直角三角形。28. 已知a、b、c满足（a﹣3）2++|c﹣5|=0．求：（1）a、b、c的值；
（2）试问以a、b、c为边能否构成三角形？若能构成三角形，求出三角形的周长；若不能构成三角形，请说明理由．
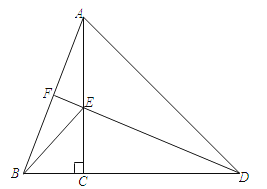
29.如图，点C在线段BD上，AC⊥BD，CA=CD，点E在线段CA上，且满足DE=AB，连接DE并延长交AB于点F．
（1）求证：DE⊥AB；
（2）若已知BC=a，AC=b，AB=c，设EF=x，则△ABD的面积用代数式可表示为；你能借助本题提供的图形，证明勾股定理吗？试一试吧．
30.如图是美国总统Garfield于1896年给出的一种验证勾股定理的办法，你能利用它证明勾股定理吗？请写出你的证明过程．（提示：如图三个三角形均是直角三角形）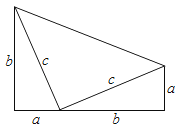
31. 在△ABC中，c为最长边．当a2+b2=c2时，△ABC是直角三角形；当a2+b2＜c2时，△ABC是钝角三角形；当a2+b2＞c2时，△ABC是锐角三角形．若a=2，b=4，试判断△ABC的形状（按角分），并求出对应的c的取值范围．32.已知：如图，AD=4，CD=3，∠ADC=90°，AB=13，BC=12．求图形的面积．
33. 已知a，b，c为△ABC的三边，且满足a2c2﹣b2c2=a4﹣b4 ， 试判定△ABC的形状．34.如图，在B港有甲、乙两艘渔船，若甲船沿北偏东60°方向以每小时8海里速度前进，乙船沿南偏东某方向以每小时15海里速度全速前进，2小时后甲船到M岛，乙船到P岛，两岛相距34海里，你知道乙船沿哪个方向航行吗？
