初中数学苏科版八年级上册3.1勾股定理同步练习

试卷更新日期：2021-06-21 类型：同步测试

进入出卷网下载

一、单选题

1. 如图，在△ABC中，AB＝6，AC＝9，AD⊥BC于D，M为AD上任一点，则MC²－MB²等于（）

A、29 B、32 C、36 D、45

查看试题解析
2. 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案，已知大正方形面积为49，小正方形面积为4，若用x，y表示直角三角形的两直角边(x＞1)，请观察图案，指出以下关系式中不正确的是（）

A、x²+y²=49 B、x－y＝2 C、2xy+4=49 D、x+y=9

查看试题解析
3. 如图，“赵爽弦图”由4个全等的直角三角形所围成，在 $R t Δ A B C$ 中， $A C = b$ ， $B C = a$ ， $∠ A C B = 90^{\circ}$ ，若图中大正方形的面积为48，小正方形的面积为6，则 ${(a + b)}^{2}$ 的值为（）

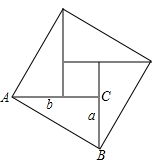A、60 B、79 C、84 D、90

查看试题解析
4. “赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a，较短直角边长为b.若ab＝8，大正方形的面积为25，则小正方形的边长为（）

A、4 B、3 C、2 D、1.5

查看试题解析
5. 如图，分别以直角三角形各边为一边向三角形外部作正方形，其中两个小正方形的面积分别为9和25，则正方形A的面积是（）

A、16 B、32 C、34 D、64

查看试题解析
6. 如图，Rt△ABC中，∠ACB=90°，若AB=15，则正方形ADEC和正方形BCFG的面积之和为（）

A、150 B、200 C、225 D、无法计算

查看试题解析
7. 如图，一棵大树在离地面3 $m$ ，5 $m$ 两处折成三段，中间一段 $A B$ 恰好与地面平行，大树顶部落在离大树底部6 $m$ 处，则大树折断前的高度是（）

A、 $9 m$ B、 $14 m$ C、 $11 m$ D、 $10 m$

查看试题解析
8. 在△ABC中，若AB=15，AC=13，高AD=12，则△ABC的周长是（）

A、42 B、32 C、42或32 D、37或33

查看试题解析
9. 在直角三角形ABC中，斜边AB=2，则AB²+BC²+AC²=（）

A、2 B、4 C、6 D、8

查看试题解析
10. 锐角△ABC中，AB=a-1，AC=a，BC=a+1（a＞4），BD⊥AC于点D.则CD-DA的值为（）

A、 $\frac{a - 2}{2}$ B、2 C、 $\frac{a - 1}{2}$ D、4

查看试题解析
11. 如图所示，已知△ABC中，AB=6，AC=9，AD⊥BC于D，M为AD上任一点，则MC²-MB²等于（）

A、9 B、35 C、45 D、无法计算

查看试题解析
12. 在△ABC中， $A B = 15 ， A C = 13$ ， $B C$ 边上的高 $A D = 12$ ，则边 $B C$ 的长为（）

A、4 B、14 C、4 或14 D、8或14

查看试题解析
13. 下列各组数中，是勾股数的是（）

A、2、3、4 B、3、4、5 C、4、5、6 D、5、6、7

查看试题解析
14. 下列各组数中，是勾股数的（）

A、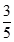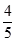，，1 B、1，2，3 C、1.5，2，2.5 D、9，40，41

查看试题解析
15.
图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．若AC=6，BC=5，将四个直角三角形中的边长为6的直角边分别向外延长一倍，得到图2所示的“数学风车”，则这个风车的外围周长是（　　）

A、51 B、49 C、76 D、无法确定

查看试题解析

二、填空题

16. 如图，在四边形 $A B C D$ 中， $∠ A B C = ∠ A D C = 90 °$ ，分别以四边向外做正方形甲、乙、丙、丁，若甲的面积为30，乙的面积为16，丙的面积为17，则丁的面积为.

查看试题解析
17. 若一直角三角形的两边长为4、5，则第三边长的平方为

查看试题解析
18. 如图，在△ABC中，∠ACB＝90°，分别以AC、AB为边长向外作正方形，且它们的面积分别为9和25，则Rt△ABC的面积为.

查看试题解析
19. 一个直角三角形三边的长a、b、c都是整数，且满足a＜b＜c，a+c=49.则b的值为.

查看试题解析
20. 直角三角形三边长分别为5，12，x，则x²=.

查看试题解析
21. 一直角三角形的斜边长比直角边长大2，另一直角边长为6，则斜边长为

查看试题解析
22. 已知直角三角形两直角边长分别为5与12，则第三边长为

查看试题解析
23. 长方形的一条对角线的长为10cm，一边长为6cm，它的面积是cm².

查看试题解析
24. 如图，学校有一块长方形花铺，有极少数人为了避开拐角走“捷径”，在花铺内走出了一条“路”.他们仅仅少走了步路(假设2步为1米)，却踩伤了花草.

查看试题解析
25. 一直角三角形两边分别为5，12，则这个直角三角形第三边的长.

查看试题解析
26. 如图，正方形ABCD的边长为2，其面积标记为S₁ ，以CD为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为S₂ ， ……按照此规律继续下去，则S₂₀₁₉的值为.

查看试题解析
27. 若一个直角三角形的其中两条边长分别为6和8，则第三边长为.

查看试题解析
28. 如图， $A B = 1.2 m$ ， $B C = 0.5 m$ ， $A D = C E = 0.2 m$ ，则加固小树的木棒DE的长是 $m .$

查看试题解析
29. 如图，在△ABC中，∠ABC＝90°，AB＝2BC＝2，在AC上截取CD＝CB．在AB上截取AP＝AD，则AP＝．

查看试题解析
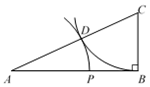30. 为了推广城市绿色出行，小蓝车公司准备在十圩港沿岸AB段建设一个共享单车停放点，该路段附近有两个广场C和D（如图），CA⊥AB于A、DB⊥AB于B，AB=4km，CA=2km，DB=1km．则停放点E应建在距点Akm处，才能使它到两广场的距离相等．

查看试题解析
31. 在Rt△ABC中， $∠ C = 90 ° ， A B = 2$ ，则 $A C^{2} + B C^{2} =$

查看试题解析

三、解答题

32. 定义：如图，点M、N把线段 $A B$ 分割成 $A M$ 、 $M N$ 和 $B N$ ，若以 $A M$ 、 $M N$ 、 $B N$ 为边的三角形是一个直角三角形，则称点M、N是线段 $A B$ 的勾股分割点.已知点M、N是线段 $A B$ 的勾股分割点，若 $A M = 2$ ， $M N = 3$ ，求 $B N$ 的长.

查看试题解析
33. 三国时代东吴数学家赵爽（字君卿，约公元3世纪）在《勾股圆方图注》一书中用割补的方法构造了“弦图”（如图1，并给出了勾股定理的证明．已知，图2中涂色部分是直角边长为 $a ， b$ ，斜边长为 $c$ 的 $4$ 个直角三角形，请根据图2利用割补的方法验证勾股定理．

查看试题解析
34. 勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小明灵感，他惊喜地发现，当四个全等的直角三角形如图摆放时，可以用“面积法"来证明 $a^{2} + b^{2} = c^{2}$ .请你写出证明过程.

查看试题解析
35. 直角三角形两直角边长分别为AB=5和BC=12，求它斜边 AC 上的高.

查看试题解析
36. 如图，将边长为a与b、对角线长为c的长方形纸片 $A B C D$ ，绕点 $C$ 顺时针旋转 $90 °$ 得到长方形 $E F G H$ ，连接 $A E$ ，则四边形 $A B G E$ 为梯形，请通过该图验证勾股定理（求证： $a^{2} + b^{2} = c^{2}$ ）.

查看试题解析
37. A，B两个居民楼在公路同侧，它们离公路的距离分别为AE＝200米，BF＝70米，它们的水平距离EF＝390米．现欲在公路旁建一个超市P，使超市到两居民楼的距离相等，则超市应建何处？为什么？

查看试题解析

四、综合题

38. 如图，在 $△ A B C$ 中， $C D ⊥ A B$ ，垂足为点 $D$ ， $A C = 20$ ， $B C = 15$ ， $D B = 9$ .

(1)、求 $C D$ 的长；

(2)、求 $A B$ 的长.

查看试题解析
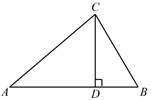39. 一个直立的火柴盒在桌面上倒下，启迪人们发现了勾股定理的一种新的证明方法.如图2，火柴盒的一个侧面ABCD倒下到AEFG的位置，连结CF，AB＝a，BC＝b，AC＝c.

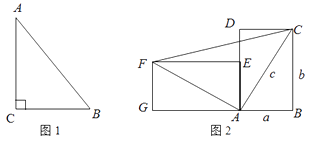(1)、请你结合图1用文字和符号语言分别叙述勾股定理；

(2)、请利用直角梯形BCFG的面积证明勾股定理： $a^{2} + b^{2} = c^{2}$ .

查看试题解析
40.
我们运用图（Ⅰ）中大正方形的面积可表示为（a+b）² ，也可表示为c³+4（ $\frac{1}{2}$ ab），即（a+b）²=c²+4（ $\frac{1}{2}$ ab）由此推导出一个重要的结论a²+b²=c² ，这个重要的结论就是著名的“勾股定理”．这种根据图形可以极简单地直观推论或验证数学规律和公式的方法，简称“无字证明”．

(1)、请你用图（Ⅱ）（2002年国际数学家大会会标）的面积表达式验证勾股定理（其中四个直角三角形的较大的直角边长都为a，较小的直角边长都为b，斜边长都为c）．

(2)、请你用（Ⅲ）提供的图形进行组合，用组合图形的面积表达式验证：（x+2y）²=x²+4xy+4y² ．

查看试题解析

初中数学苏科版八年级上册3.1勾股定理 同步练习

一、单选题

二、填空题

三、解答题

四、综合题

初中数学苏科版八年级上册3.1勾股定理同步练习