初中数学苏科版八年级上册2.5等腰三角形的轴对称性 同步练习
试卷更新日期：2021-06-21 类型：同步测试
一、单选题
-
1. 在等腰三角形ABC中，∠A=80°.则∠B的度数不可能为（ ）A、20° B、40° C、50° D、80°2. 如图，在△ABC中，AB=AC，AD为BC边上的高，点E为AC的中点，连接DE，若△ABC的周长为20，则△CDE的周长为（ ）
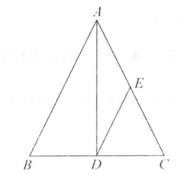A、10 B、12 C、14 D、163. 如图，在 中，DE是AB的垂直平分线，且分别交AB、AC于点D和E， =50°， =60°，则 为（ ）
A、30° B、20° C、25° D、35°4. 如图，△ABC是等边三角形，BD⊥AB，且AB=BD，则∠ACD的度数为（ ）
A、30° B、35° C、45° D、50°5. 如图，已知Rt△ABC中，∠C＝90º，∠A＝30º，在直线BC或AC上取一点P，使得△PAB是等腰三角形，则符合条件的P点有（ ）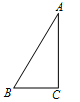
A、5个 B、6个 C、7个 D、8个6. 下列说法中，正确的是（ ）A、等腰三角形底边上的中线就是底边的垂直平分线 B、等腰三角形的对称轴是底边上的高 C、一条线段可看做是以它的垂直平分线为对称轴的轴对称图形 D、等腰三角形的对称轴就是顶角平分线7. 等腰三角形的一个外角是100°，则其底角是（ ）A、80°或20° B、80°或50° C、80° D、50°8. 已知等腰三角形的周长为29，其中一边长为7，则该等腰三角形的底边长为（ ）A、11 B、7 C、15 D、15或79. 如图，D是△ABC中BC边上一点，AB=AC=BD，则∠1和∠2的关系是（ ）
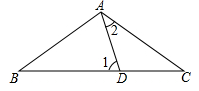A、180°+∠2=3∠1 B、∠1+∠2=90° C、180°－∠1=3∠2 D、∠1=2∠210. 如图，△ABC中，AB= 4，AC= 7，BD，CD分别平分∠ABC，∠ACB，过点D作直线平行于BC，交AB，AC于E，F，则△AEF的周长为（ ）
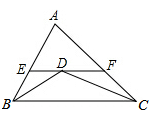A、9 B、11 C、15 D、18二、填空题
-
11. 等腰三角形的两条边长为4和9，则该等腰三角形的周长为.12. 已知△ABC的三边长分别为4、4、6，在△ABC所在平面内画一条直线，将△ABC分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画 条.
13. 如图，△ABC中，∠B、∠C的平分线交于点O，过O点作EF∥BC交AB、AC于E、F，EF=5，BE=2，则CF=.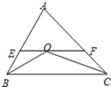
14. 如图，在 中， ， ，则 的度数为.
15. 等腰三角形的一个外角是80°，则其底角是度.16. 若等腰三角形的一个角为110°，则它的底角为度.17. 如图，在△PAB中，PA=PB，M、N、K分别是PA、PB、AB上的点，且AM= BK ，BN=AK.若∠MKN=50°，则∠P的度数为.
18. 在△ABC中，AB=AC，其周长为20cm，若AB=8cm，则BC=cm.19. 如图，等边△ABC的边长为2，BD为高，延长BC到点E，使CE＝CD，则DE长为.
20. 如图，△ABC为等边三角形，BD⊥AB，BD=AB，则∠DCB= .
三、解答题
-
21. 如图，四边形 中， ， ，求证： .
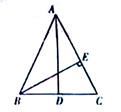
22. 如图，Rt△ABC中，∠CAB＝90°，∠ACB＝30°，D是AB上一点（不与A、B重合），DE⊥BC于E，若P是CD的中点，请判断△PAE的形状，并说明理由.
23. 如图，在∆ABC中，AB＝AC，AD是BC边上的中线，BE⊥AC于点E.求证：∠CBE=∠BAD.
24. 如图，等边△ABC中，D是AC的中点，E是BC延长线上的一点，且CE=CD，DF⊥BE，垂足是F，求证：BF=EF．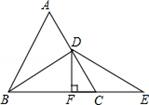
25. 如图，△ABC是等边三角形，AD为中线，AD=AE，E在AC上，求∠EDC的度数．
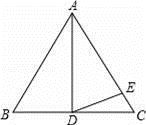26. 如图：已知等边△ABC中，D是AC的中点，E是BC延长线上的一点，且CE=CD，DM⊥BC，垂足为M，求证：M是BE的中点．
四、作图题
-
27.
如图，△ABC和△DCE都是等边三角形，且点C是线段AD的中点，请仅用无刻度直尺完成以下作图：
（1）作BC的中点P；
（2）过点C作AD的垂线．
五、综合题
-
28. 如图，在△ABC中，∠ABC与∠ACB的平分线交于点O，过点O作DE∥BC，分别交AB、AC于点D、E.
(1)、△BDO是等腰三角形吗？请说明理由.(2)、若AB=10，AC=6，求△ADE的周长.29. 如图，在△ABC中，AE是∠BAC的角平分线，交BC于点E，DE∥AB交AC于点D.
(1)、求证AD=ED；(2)、若AC=AB，DE=3，求AC的长.30. 已知等腰三角形的周长为16,(1)、若腰长为6,求它的底边长.(2)、若一边长为6,求它的另外两边的长.31. 如图，在△ABC中，∠ABC与∠ACB的平分线相交于点O，过点O作DE//BC分别交AB，AC于点D，E．
(1)、求证：OD=DB．
(2)、若DE=5，求DB+CE的值．32. 如图，在等腰△ABC中，AB=AC，BD为高．（从下列问题中任选一问作答）
(1)、若∠ABD+∠C=120°，求∠A的度数；(2)、若CD=3，BC=5，求△ABC的面积．33. 如图，△ABD是等腰三角形，AB=AD，将△ABD沿BD翻折得△CBD，点P是线段BD上一点，(1)、如图1，连接PA、PC，求证：CP=AP；
(2)、如图2，连接PA，若∠BAP=90°时，作∠DPF=45°，线段PF交线段CD于F，求证：AD=AP+DF；
(3)、如图3，∠ABD=30°，连接AP并延长交CD于M，若∠BAM=90°，在BD上取一点Q，且DQ=3BQ，连BM、CQ，当BM= 时，求CQ的长．
34.如图，在△ABC中，BC=10cm，BP、CP分别是∠ABC和∠ACB的角平分线，PD∥AB，PE∥AC．
(1)、求证：BD=PD(2)、求△PDE的周长．35.如图，AD∥BC，∠BAC=70°，DE⊥AC于点E，∠D=20°．
(1)、求∠B的度数，并判断△ABC的形状(2)、若延长线段DE恰好过点B，试说明DB是∠ABC的平分线．36.如图，△ABC中，∠A=36°，∠C=72°，∠DBC=36°．
(1)、求∠1的度数(2)、求证：BC=BD=AD．37.已知：如图，在△ABC中，AD⊥BC，垂足为点D，BE⊥AC，垂足为点E，M为AB边的中点，连接ME、MD、ED．
(1)、求证：△MED为等腰三角形(2)、求证：∠EMD=2∠DAC．
-
