初中数学苏科版八年级上册2.4线段、角的轴对称性 同步练习
试卷更新日期:2021-06-21 类型:同步测试
一、单选题
-
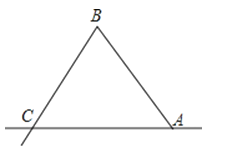
1. 三名同学分别站在一个三角形三个顶点的位置上,他们在玩抢凳子的游戏,要求在他们中间放一个凳子,抢到凳子者获胜,为使游戏公平,凳子应放的最适当的位置在三角形的( )A、三条角平分线的交点 B、三边中线的交点 C、三边上高所在直线的交点 D、三边的垂直平分线的交点2. A、B、C分别表示三个村庄,AB=1000米,BC=600米,AC=800米,为拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )A、AB中点 B、BC中点 C、AC中点 D、∠C的平分线与AB的交点3. 图,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,AC=2,则S△ABE的值是( )
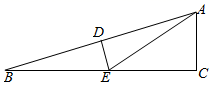 A、4 B、5 C、6 D、84. 如图,在 Rt△ACB 中,∠C=90°, AD 平分∠CAB 交BC平D,DE ⊥AB 交AB于E,则下列结论中不正确的是( )
A、4 B、5 C、6 D、84. 如图,在 Rt△ACB 中,∠C=90°, AD 平分∠CAB 交BC平D,DE ⊥AB 交AB于E,则下列结论中不正确的是( ) A、BD +ED=BC B、DE 平分∠ADB C、AD 平分∠EDC D、ED+AC>AD5. 如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E.已知PE=10,则点P到AB的距离是( )
A、BD +ED=BC B、DE 平分∠ADB C、AD 平分∠EDC D、ED+AC>AD5. 如图,点P是∠BAC的平分线AD上一点,PE⊥AC于点E.已知PE=10,则点P到AB的距离是( )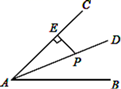 A、15 B、12 C、5 D、106. 如图,DE是△ABC的边AB的垂直平分线,点D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长是( )
A、15 B、12 C、5 D、106. 如图,DE是△ABC的边AB的垂直平分线,点D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长是( ) A、12 B、13 C、14 D、157. 如图,△ABC 中,AB = 6cm ,AC = 8cm ,BC 的垂直平分线l 与 AC 相交于点 D ,则DABD 的周长为( )
A、12 B、13 C、14 D、157. 如图,△ABC 中,AB = 6cm ,AC = 8cm ,BC 的垂直平分线l 与 AC 相交于点 D ,则DABD 的周长为( ) A、10cm B、12cm C、14cm D、16cm8. 如图,在 ABC中,AC=4cm,线段AB的垂直平分线交AC于点N, BCN的周长是7cm,则BC的长为( )
A、10cm B、12cm C、14cm D、16cm8. 如图,在 ABC中,AC=4cm,线段AB的垂直平分线交AC于点N, BCN的周长是7cm,则BC的长为( ) A、3 B、4 C、7 D、119.
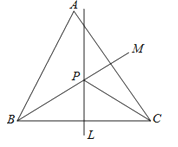
A、3 B、4 C、7 D、119.如图,锐角三角形ABC中,直线L为BC的中垂线,直线M为∠ABC的角平分线,L与M相交于P点.若∠A=60°,∠ACP=24°,则∠ABP的度数为何?( )
 A、24° B、30° C、32° D、36°10. 若P是△ 所在平面内的点,且 ,则下列说法正确的是( )A、点P是△ 三边垂直平分线的交点 B、点P是△ 三条角平分线的交点 C、点P是△ 三边上高的交点 D、点P是△ 三边中线的交点11. 如图,DE是AC边的垂直平分线,AB=5cm,BC=4cm.那△BEC的周长是( )
A、24° B、30° C、32° D、36°10. 若P是△ 所在平面内的点,且 ,则下列说法正确的是( )A、点P是△ 三边垂直平分线的交点 B、点P是△ 三条角平分线的交点 C、点P是△ 三边上高的交点 D、点P是△ 三边中线的交点11. 如图,DE是AC边的垂直平分线,AB=5cm,BC=4cm.那△BEC的周长是( ) A、9cm B、8cm C、7cm D、6cm12. 在联欢会上,有 、 、 三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在 的( )A、三边中线的交点 B、三条角平分线的交点 C、三边中垂线的交点 D、三边上高所在直线的交点13. 如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于( )
A、9cm B、8cm C、7cm D、6cm12. 在联欢会上,有 、 、 三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在 的( )A、三边中线的交点 B、三条角平分线的交点 C、三边中垂线的交点 D、三边上高所在直线的交点13. 如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于( )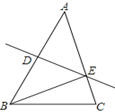 A、8cm B、10cm C、12cm D、14cm14. 如图, 中, , 平分 , 于点 , 于点 , ,则 的长为( )
A、8cm B、10cm C、12cm D、14cm14. 如图, 中, , 平分 , 于点 , 于点 , ,则 的长为( )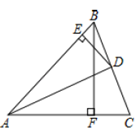 A、3 B、4 C、5 D、615. 在联欢会上,有A,B,C三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在△ABC的( )A、三边中线的交点 B、三条角平分线的交点 C、三边上高的交点 D、三边垂直平分线的交点16. 如图,在△ABC中,AC的垂直平分线交AC于点E,交BC于点D,△ABD的周长为16cm,AC为5cm,则△ABC的周长为( )
A、3 B、4 C、5 D、615. 在联欢会上,有A,B,C三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在△ABC的( )A、三边中线的交点 B、三条角平分线的交点 C、三边上高的交点 D、三边垂直平分线的交点16. 如图,在△ABC中,AC的垂直平分线交AC于点E,交BC于点D,△ABD的周长为16cm,AC为5cm,则△ABC的周长为( )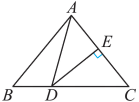 A、24cm B、21cm C、20cm D、无法确定
A、24cm B、21cm C、20cm D、无法确定二、填空题
-
17. 如图, 是 的角平分线, ,则点 到 的距离为.
 18. 如图所示,△ABC中,∠C=90°,AD平分∠BAC,AB=6,CD=2,则△ABD的面积是.
18. 如图所示,△ABC中,∠C=90°,AD平分∠BAC,AB=6,CD=2,则△ABD的面积是. 19. 如图, 中, , 的平分线交BC于点D, 于点E, ,则 面积是.
19. 如图, 中, , 的平分线交BC于点D, 于点E, ,则 面积是. 20. 如图,在Rt△ABC中,∠C=90°,AB=6,AD平分∠BAC,交BC边于点D,若CD=1,则△ABD的面积为.
20. 如图,在Rt△ABC中,∠C=90°,AB=6,AD平分∠BAC,交BC边于点D,若CD=1,则△ABD的面积为. 21. 如图,在 中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,且 与 的周长分别是16和10,则AB的长为
21. 如图,在 中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,且 与 的周长分别是16和10,则AB的长为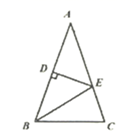 22. 如图,△ABC中,AB=AC=14cm,BC=10cm,AB的垂直平分线MN交AC于点D,则△CBD的周长C△BCD=.
22. 如图,△ABC中,AB=AC=14cm,BC=10cm,AB的垂直平分线MN交AC于点D,则△CBD的周长C△BCD=. 23. 如图,△ABC中,∠C=90°,AD是角平分线,若CD=2,则点D到AB的距离等于.
23. 如图,△ABC中,∠C=90°,AD是角平分线,若CD=2,则点D到AB的距离等于. 24. 如图,在△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为13cm,则△ABC的周长为cm.
24. 如图,在△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为13cm,则△ABC的周长为cm.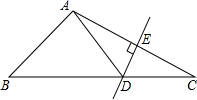 25. 如图,△ABC的边BC的垂直平分线MN交AC于D,若△ADB的周长是10cm,AB=3cm,则AC=cm.
25. 如图,△ABC的边BC的垂直平分线MN交AC于D,若△ADB的周长是10cm,AB=3cm,则AC=cm. 26. 如图,在Rt△ABC中,∠C=90°,AB=12,AD平分∠BAC交BC于点D,若CD=4,则△ABD的面积为.
26. 如图,在Rt△ABC中,∠C=90°,AB=12,AD平分∠BAC交BC于点D,若CD=4,则△ABD的面积为.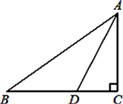 27. 如图,在△ABC中,∠C = 90°,AD平分∠BAC,且CD = 5,则点D到AB的距离为.
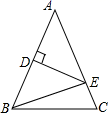
27. 如图,在△ABC中,∠C = 90°,AD平分∠BAC,且CD = 5,则点D到AB的距离为. 28. 如图,△ABC中,∠A=100°,∠B=20°,边BC的垂直平分线分别交AB、BC于点E、D,则∠ACE的度数等于.
28. 如图,△ABC中,∠A=100°,∠B=20°,边BC的垂直平分线分别交AB、BC于点E、D,则∠ACE的度数等于. 29. 如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上一个动点,若PA=2,则PQ的最小值为.
29. 如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上一个动点,若PA=2,则PQ的最小值为.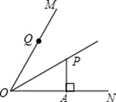
三、解答题
-
30. 已知△ABC中,AB=AC=8,DE垂直平分AB,交AC于E.已知△BEC的周长是13,求△ABC的周长.
 31. 已知:如图,△ABC的两内角∠ABC、∠ACB的角平分线相交于点P.求证:点P在∠A的角平分线上.
31. 已知:如图,△ABC的两内角∠ABC、∠ACB的角平分线相交于点P.求证:点P在∠A的角平分线上.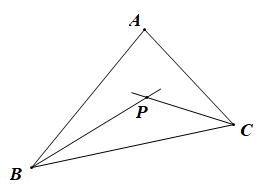 32. 如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.若BC=13cm,则△ADE周长是多少?
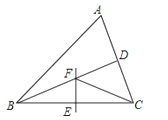
32. 如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.若BC=13cm,则△ADE周长是多少? 33. 如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.
33. 如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.(1)若∠A=60°,∠ABD=24°,求∠ACF的度数;
(2)若EF=4,BF:FD=5:3,S△BCF=10,求点D到AB的距离.
 34.
34.如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C,D.
(1)∠ECD和∠EDC相等吗?
(2)OC和OD相等吗?
(3)OE是线段CD的垂直平分线吗?
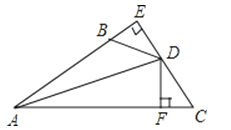
 35. 如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
35. 如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.
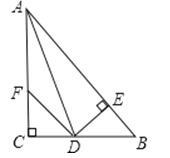
 36. 如图:在△ABC中,∠C=90° AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
36. 如图:在△ABC中,∠C=90° AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;说明:(1)CF=EB.
(2)AB=AF+2EB.
 37.
37.现要在三角地ABC内建一中心医院,使医院到A、B两个居民小区的距离相等,并且到公路AB和AC的距离也相等,请确定这个中心医院的位置.