江苏省无锡市江阴市2020-2021学年高三上学期数学开学检测试卷
试卷更新日期:2021-06-18 类型:开学考试
一、单选题
-
1. 已知集合 ,则 ( )A、 B、 C、 D、2. 命题“ ”的否定是( )A、 B、 C、 D、3. 设 ,则 =( )A、0 B、 C、1 D、4. 已知等差数列{an}前9项的和为27,a10=8,则a100=( )A、100 B、99 C、98 D、975. 若非零向量 、 满足 且 ,则 与 的夹角为( )A、 B、 C、 D、6. 函数 的图象大致为( )A、
 B、
B、 C、
C、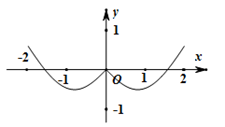 D、
D、 7. 已知函数 为自然对数的底数 ,若 ,则( )A、 B、 C、 D、8. 2020年新型冠状病毒肺炎蔓延全国,作为主要战场的武汉,仅用了十余天就建成了“小汤山”模式的火神山医院和雷神山医院,再次体现了中国速度.随着疫情发展,某地也需要参照“小汤山”模式建设临时医院,其占地是出一个正方形和四个以正方形的边为底边、腰长为400m的等腰三角形组成的图形(如图所示),为使占地面积最大,则等腰三角形的底角为( )
7. 已知函数 为自然对数的底数 ,若 ,则( )A、 B、 C、 D、8. 2020年新型冠状病毒肺炎蔓延全国,作为主要战场的武汉,仅用了十余天就建成了“小汤山”模式的火神山医院和雷神山医院,再次体现了中国速度.随着疫情发展,某地也需要参照“小汤山”模式建设临时医院,其占地是出一个正方形和四个以正方形的边为底边、腰长为400m的等腰三角形组成的图形(如图所示),为使占地面积最大,则等腰三角形的底角为( ) A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
9. 给出下列命题,其中正确命题为( ).A、若样本数据 , ,…, 的方差为2,则数据 , ,…, 的方差为4 B、回归方程为 时,变量 与 具有负的线性相关关系 C、随机变量 服从正态分布 , ,则 D、相关指数 来刻画回归的效果, 值越大,说明模型的拟合效果越好10. 下面的命题正确的有( ).A、方向相反的两个非零向量一定共线 B、单位向量都相等 C、若 , 满足 且 与 同向,则 D、“若 、 、 、 是不共线的四点,且 ” “四边形 是平行四边形”11. 下列函数中,既是奇函数又在区间 上单调递增的是( ).A、 B、 C、 D、12. 已知 的最小正周期为 ,则下列说法正确的有( )A、 B、函数 在 上为增函数 C、直线 是函数 图象的一条对称轴 D、 是函数 图象的一个对称中心
三、填空题
-
13. 的展开式中, 的系数是 .14. 设曲线 在点(0,1)处的切线与曲线 上点 处的切线垂直,则 的坐标为 .15. “勾3股4弦5”是勾股定理的一个特例.根据记载,西周时期的数学家商高曾经和周公讨论过“勾3股4弦5”的问题,毕达哥拉斯发现勾股定理早了500多年,如图,在矩形 中, 满足“勾3股4弦5”,且 , 为 上一点, .若 ,则 的值为.
 16. 已知长方体 的顶点都在球 的表面上,且 ,则球 的表面积为.若 与 所成的角为 ,则 与 所成角的余弦值为.
16. 已知长方体 的顶点都在球 的表面上,且 ,则球 的表面积为.若 与 所成的角为 ,则 与 所成角的余弦值为.四、解答题
-
17. 在平面四边形 中,(1)、求 ;(2)、若 求 .18. 已知等差数列 满足 , .(1)、求数列 的通项公式;(2)、设数列 满足 ,求数列 的前 项和 .19. 第23届冬季奥运会于2018年2月9日至2月25日在韩国平昌举行,期间正值我市学校放寒假,寒假结束后,某校工会对全校教职工在冬季奥运会期间每天收看比赛转播的时间作了一次调查,得到如下频数分布表:
收看时间(单位:小时)
收看人数
14
30
16
28
20
12
附表及公式:
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
.
(1)、若将每天收看比赛转播时间不低于3小时的教职工定义为“体育达人”,否则定义为“非体育达人”,请根据频数分布表补全 列联表:男
女
合计
体育达人
40
非体育达人
30
合计
并判断能否有90%的把握认为该校教职工是否为“体育达人”与“性别”有关;
(2)、在全校“体育达人”中按性别分层抽样抽取6名,再从这6名“体育达人”中选取2名作冬奥会知识讲座.求抽取的这两人恰好是一男一女的概率.20. 如图 ,在直角梯形 中, , , , , 是 的中点, 是 与 的交点.将 沿 折起到 的位置,如图2. (1)、证明: 平面 ;(2)、若平面 平面 ,求平面 与平面 夹角的余弦值.21. 为评估设备 生产某种零件的性能,从设备 生产零件的流水线上随机抽取 个零件作为样本,测量其直径后,整理得到下表:
(1)、证明: 平面 ;(2)、若平面 平面 ,求平面 与平面 夹角的余弦值.21. 为评估设备 生产某种零件的性能,从设备 生产零件的流水线上随机抽取 个零件作为样本,测量其直径后,整理得到下表:直径
58
59
61
62
63
64
65
66
67
68
69
70
71
73
合计
个数
1
1
3
5
6
19
33
18
4
4
2
1
2
1
100
经计算,样本直径的平均值 ,标准差 ,以频率值作为概率的估计值.
(1)、为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为 ,并根据以下不等式进行评判( 表示相应事件的概率):① ;② ;③ .评判规则为:若同时满足上述三个不等式,则设备等级为甲;若仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部都不满足,则等级为丁,试判断设备 的性能等级.(2)、将直径小于等于 或直径大于 的零件认为是次品.①从设备 的生产流水线上随机抽取 件零件,计算其中次品件数 的数学期望 ;
②从样本中随机抽取 件零件,计算其中次品件数 的概率分布列和数学期望 .
22. 已知函数 , 且 的导函数为 .(1)、求函数 的极大值;(2)、若函数 有两个零点 , ,求 的取值范围.