四川省天府名校2021届高三下学期理数4月诊断性考试试卷
试卷更新日期:2021-06-18 类型:月考试卷
一、单选题
-
1. 已知集合 ,集合 ,则 ( )A、 B、 C、 D、2. 已知复数 满足: ,则 ( )A、 B、 C、1 D、3. 已知角 的终边绕原点 逆时针旋转 后,得到角 的终边,角 的终边过点 ,且 ,则 的值为( )A、 B、 C、 D、4. 宋代学者聂崇义编撰的《三礼图集注》中描述的周王城,“匠人营国,方九里,旁三门,国中九经九纬……”;意思是周王城为正方形,边长为九里,每边都有左中右三个门;城内纵横各有九条路……;则依据此种描述,画出周王城的平面图,则图中共有( )个矩形
 A、3025 B、2025 C、1225 D、25255. 设抛物线 : 的焦点为 ,准线为 , 为抛物线 上一点,以 为圆心的圆 与准线 相切,且过点 ,则抛物线的方程为( )A、 B、 C、 D、 或6. 已知 , 为不同直线, , 为不同平面,则下列结论不正确的是( )A、若 , ,则 B、若 , ,则直线 平面 C、若 , , ,则 D、若 , , ,则7. 设 , , ,则 , , 的大小关系是( )A、 B、 C、 D、8. 若变量 , 满足约束条件 ,且 的最小值是-2,则 的值为( )A、 B、-2 C、 D、-19. 函数 的图象在 上恰有两个极大值点,则 的取值范围为( )A、 B、 C、 D、10. 在 中, , 平分 交 于 ,且 ,则 的面积的最小值为( )A、3 B、 C、4 D、11. 已知三棱锥 的棱长均为1,现将三棱锥 绕着 旋转,则 所经过的区域构成的几何体的体积为( )A、 B、 C、 D、12. 定义函数 ,若函数 , ,且对任意的 ,都有 成立,函数 的图象与 自左向右有四个交点 、 、 、 ,则 的范围为( )A、 B、 C、 D、
A、3025 B、2025 C、1225 D、25255. 设抛物线 : 的焦点为 ,准线为 , 为抛物线 上一点,以 为圆心的圆 与准线 相切,且过点 ,则抛物线的方程为( )A、 B、 C、 D、 或6. 已知 , 为不同直线, , 为不同平面,则下列结论不正确的是( )A、若 , ,则 B、若 , ,则直线 平面 C、若 , , ,则 D、若 , , ,则7. 设 , , ,则 , , 的大小关系是( )A、 B、 C、 D、8. 若变量 , 满足约束条件 ,且 的最小值是-2,则 的值为( )A、 B、-2 C、 D、-19. 函数 的图象在 上恰有两个极大值点,则 的取值范围为( )A、 B、 C、 D、10. 在 中, , 平分 交 于 ,且 ,则 的面积的最小值为( )A、3 B、 C、4 D、11. 已知三棱锥 的棱长均为1,现将三棱锥 绕着 旋转,则 所经过的区域构成的几何体的体积为( )A、 B、 C、 D、12. 定义函数 ,若函数 , ,且对任意的 ,都有 成立,函数 的图象与 自左向右有四个交点 、 、 、 ,则 的范围为( )A、 B、 C、 D、二、填空题
-
13. 若 ,若 ,则 .14. 在边长为2的等边 中, 为 的中点, , 是线段 的三等分点,则 = .15. 等边 的边长为2,点 为 的中点,将 沿 折起到 ,使得 ,若该三棱锥的所有顶点都在同一个球面上,则该球的表面积为 .16. 已知点 , 是椭圆 : 与双曲线 : ( , )的公共焦点, , 分别是 和 的离心率,点 是 和 在第一象限的公共点,且 ,若 时,则 .
三、解答题
-
17. 在正项等比数列 中, ,且 , , 是等差数列 的前三项.(1)、求数列 和 的通项公式;(2)、设 ,求数列 的前 项和 .18. 某地盛产橙子,但橙子的品质与当地的气象相关指数 有关,气象相关指数入 越高,橙子品质越高,售价同时也会越高.某合作社统计了近10年的当地的气象相关指数 ,得到了如下频率分布直方图.
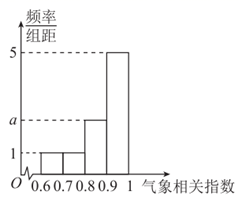 (1)、求 的值;(2)、从近10年中任意抽取3年研究气象指数 对橙子品质的影响,求这3年的气象相关指数 在 之间的个数 的数学期望;(3)、根据往年数据,该合作社的利润 (单位:千元,利润=收入-投入)与每亩地的投入 (单位:千元)和气象相关指数 的关系如下: , ,气象相关指数 取何值时,能使对于任意的 时该合作社都不亏损.19. 如图所示,几何体 中,四边形 为菱形, 平面 , , , , ,平面 与平面 的交线为 .
(1)、求 的值;(2)、从近10年中任意抽取3年研究气象指数 对橙子品质的影响,求这3年的气象相关指数 在 之间的个数 的数学期望;(3)、根据往年数据,该合作社的利润 (单位:千元,利润=收入-投入)与每亩地的投入 (单位:千元)和气象相关指数 的关系如下: , ,气象相关指数 取何值时,能使对于任意的 时该合作社都不亏损.19. 如图所示,几何体 中,四边形 为菱形, 平面 , , , , ,平面 与平面 的交线为 .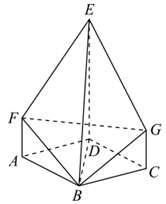 (1)、证明:直线 平面 ;(2)、求直线 与平面 所成角的正弦值的范围.20. 已知椭圆 : 的左焦点为 ,过点 作 轴的垂线与椭圆在第二象限的交点为 .椭圆的左、右顶点分别为 , ,已知 的面积为 , .(1)、求椭圆 的标准方程;(2)、直线 与 轴交于点 ,过点 作直线与椭圆交于 , 两点,若 .求直线 的方程.
(1)、证明:直线 平面 ;(2)、求直线 与平面 所成角的正弦值的范围.20. 已知椭圆 : 的左焦点为 ,过点 作 轴的垂线与椭圆在第二象限的交点为 .椭圆的左、右顶点分别为 , ,已知 的面积为 , .(1)、求椭圆 的标准方程;(2)、直线 与 轴交于点 ,过点 作直线与椭圆交于 , 两点,若 .求直线 的方程.