江苏省泰州市2021届高三下学期数学考前练笔试卷

试卷更新日期：2021-06-18 类型：开学考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | x^{2} - x - 2 \leq 0}$ ， $B = {x | 2 - x > 0}$ ，则 $A \cap B =$ （）

A、 $[- 1, 2)$ B、 $(- 1, 2)$ C、 $(- 1, 2]$ D、 $(- \infty, - 1)$

查看试题解析
2. 由数据 $(x_{1}, y_{1}), (x_{2}, y_{2}), \dots, (x_{10}, y_{10})$ 可得 $y$ 关于 $x$ 的线性回归方程为 $\hat{y} = x + 3.5$ ，若 $\sum_{i = 1}^{10} x_{i} = 15$ ，则 $\sum_{i = 1}^{10} y_{i} =$ （）

A、18.5 B、50 C、60 D、100

查看试题解析
3. 已知向量 $\vec{a} = (1, 2)$ ， $\vec{b} = (2, - 2)$ ， $\vec{c} = (1, λ)$ ，若 $\vec{c} ⊥ (2 \vec{a} + \vec{b})$ ，则实数 $λ =$ （）

A、2 B、 $\frac{1}{2}$ C、 $- \frac{1}{2}$ D、 $- 2$

查看试题解析
4. 马林·梅森(MarinMersenne ， 1588-1648)是17世纪法国数学家．他在欧几里得、费马等人研究的基础上深入地研究了 $2^{p} - 1$ 型的数．人们为纪念梅森在数论方面的这一贡献，将形如 $2^{p} - 1$ (其中 $p$ 是素数)的素数，称为梅森素数．在不超过20的素数中，随机选取两个不同的数，至少有一个为梅森素数的概率是（）

A、 $\frac{3}{7}$ B、 $\frac{5}{12}$ C、 $\frac{13}{28}$ D、 $\frac{19}{55}$

查看试题解析
5. 已知曲线 $C_{1} ： x^{2} + y^{2} - 4 x - 6 y + 12 = 0$ 与曲线 $C_{2} ： (y - 4) (3 x + 4 y - m) = 0$ 恰有三个不同的公共点，则实数 $m$ 的取值范围为（）

A、 $(13 ， 22)$ B、 $(22 ， 23)$ C、 $(13 ， 23)$ D、 $(13 ， 22) \cup (22 ， 23)$

查看试题解析
6. 将函数 $y = f (x)$ 的图象向右平移 $\frac{π}{3}$ 个单位后得到一个奇函数的图象，则该函数的解析式可能为（）

A、 $f (x) = \sin (2 x + \frac{π}{3})$ B、 $f (x) = \sin (x - \frac{π}{6})$ C、 $f (x) = \cos (2 x - \frac{π}{3})$ D、 $f (x) = \cos (2 x + \frac{π}{6})$

查看试题解析
7. 如图是一款多功能粉碎机的实物图，它的进物仓为正四棱台，已知该四棱台的上底面棱长为 $48 cm$ ，下底面棱长为 $8 cm$ ，侧棱长为 $25 \sqrt{2} cm$ ，则该款粉碎机进物仓的体积为（） ${cm}^{3}$

A、 $11840 \sqrt{2}$ B、 $13760 \sqrt{2}$ C、 $35520 \sqrt{2}$ D、 $41280 \sqrt{2}$

查看试题解析
8. 已知函数 $f (x) = \frac{1}{2^{| x |}} - \frac{1}{2} | x |$ ，则 $f (x) f (x + 2) \leq 0$ 的解集为（）

A、 $[- 3, 1]$ B、 $[- 1, 1]$ C、 $[- 3, - 1]$ D、 $[- 3, + \infty)$

查看试题解析

二、多选题

9. 某公司对三名毕业生的九项能力进行指标测试（每项指标总分为1，分值高者为优），根据雷达图判断下列说法合理的有（）

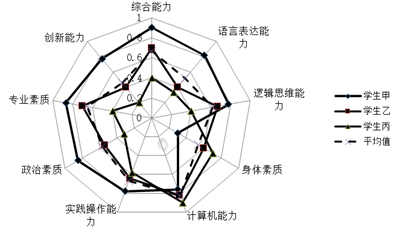A、学生甲各项素质和能力都比较突出 B、学生乙各项素质和能力相对处于中等水平 C、学生乙需要提高语言表达能力 D、学生丙各项能力都有待提高

查看试题解析
10. 设 $z$ 为复数，在复平面内 $z$ 、 $\bar{z}$ 对应的点分别为 $P$ 、 $Q$ ，坐标原点为 $O$ ，则下列命题中正确的有（）

A、当 $z$ 为纯虚数时， $P, O, Q$ 三点共线 B、当 $z = 1 + i$ 时， $△ P O Q$ 为等腰直角三角形 C、对任意复数 $z$ ， $\vec{O P} \neq \vec{O Q}$ D、当 $z$ 为实数时， $\vec{O P} = \vec{O Q}$

查看试题解析
11. 已知函数 $f (x) = \sin π x + \cos x$ ，则下列说法正确的有（）

A、 $2 π$ 是 $f (x)$ 的一个周期 B、 $| f (x) | < 2$ C、 $f (x)$ 的最大值为2 D、存在正实数t ，使得 $f (x)$ 在 $[0 ， t]$ 上为增函数

查看试题解析
12. 已知 $c > a$ ，若函数 $f (x) = x^{2} - 2 x + b$ 有两个零点 $c ， d$ ， $g (x) = | \ln x | - d$ 有两个零点 $a ， b$ ，则下列选项正确的有（）

A、 $d < b < 1$ B、 $a + b > 2 c d$ C、 $a d > b c$ D、 $\log_{a} c > \log_{b} d$

查看试题解析

三、填空题

13. 已知等差数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，公差为整数，现有四个等式：① $a_{2} = 3$ ；② $a_{5} = 8$ ；③ $S_{3} = 9$ ；④ $S_{5} = 25$ ，若其中有且只有一个等式不成立，则 $S_{10} =$ ．

查看试题解析
14. 抛物线 $C$ ： $y^{2} = 8 x$ 的焦点为 $F$ ，点 $A$ 为 $C$ 上的一点，若 $| F A | = 8$ ，则直线 $F A$ 的倾斜角为．

查看试题解析
15. 由两种或三种正多边形面组成的凸多面体称作阿基米德多面体．将一个棱长为12的正四面体截去4个小正四面体后可以得到一个由正三角形和正六边形构成的阿基米德八面体，则该阿基米德八面体的外接球的表面积为．

查看试题解析
16. 对任意的 $α \in (0, \frac{π}{4})$ ， $β \in (0, \frac{π}{4})$ ，满足 $\sin β = \cos (2 α + β)$ ，则 $3 t a n α + 2 \tan β$ 的最小值为．

查看试题解析

四、解答题

17. 已知数列 ${a_{n}}$ 的前 $n$ 项之积为 $T_{n}$ ．

(1)、若 ${a_{n}}$ 为等比数列， $T_{2} = 3$ ， $T_{3} = 27$ ，求 $T_{n}$ ；

(2)、若 ${T_{n}}$ 为等比数列， $T_{2} = 3$ ， $T_{3} = 27$ ，求数列 ${a_{n}}$ 的前 $n$ 项和 $S_{n}$ ．

查看试题解析
18. 在 $△ A B C$ 中， $D$ 是边 $B C$ 上一点， $A B ⊥ A D$ ， $B D = 4$ ， $C D = 1$ ．

(1)、若 $∠ B = \frac{π}{4}$ ，求 $A C$ 的长；

(2)、若 $∠ C A D = \frac{π}{6}$ ，求 $A C$ 的长．

查看试题解析
19. 在正四棱锥 $P - A B C D$ 中， $A B = 2$ ， $P A = \sqrt{6}$ ， $E ， F$ 分别是 $A B ， A D$ 的中点，过直线 $E F$ 的平面 $α$ 分别与侧棱 $P B ， P D$ 交于点 $M ， N$ ．

(1)、求证： $M N / / B D$ ；

(2)、若 $E F = 2 M N$ ，求直线 $P A$ 与平面 $α$ 所成角的正弦值．

查看试题解析
20. 已知椭圆 $P : \frac{x^{2}}{4} + y^{2} = 1$ 的右顶点为 $A$ ，点 $M (x_{0}, y_{0})$ 是椭圆 $P$ 上异于 $A$ 的一点， $M N ⊥ x$ 轴于点 $N$ ， $B$ 是 $M N$ 的中点，过动点 $M (x_{0}, y_{0})$ 的直线 $l : x_{0} x + 4 y_{0} y = 4$ 与直线 $A B$ 交于点 $C$ ．

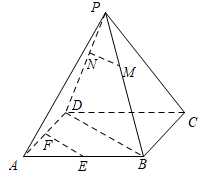(1)、当 $x_{0} = \frac{6}{5}$ 时，求证：直线l与椭圆 $P$ 只有一个公共点；

(2)、求证：点 $C$ 在定直线上运动．

查看试题解析
21. 现有一批疫苗试剂，拟进入动物试验阶段，将1000只动物平均分成100组，任选一组进行试验．第一轮注射，对该组的每只动物都注射一次，若检验出该组中有9只或10只动物产生抗体，说明疫苗有效，试验终止；否则对没有产生抗体的动物进行第二轮注射，再次检验．如果被二次注射的动物都产生抗体，说明疫苗有效，否则需要改进疫苗．设每只动物是否产生抗体相互独立，两次注射疫苗互不影响，且产生抗体的概率均为 $p (0 < p < 1)$ ．

(1)、求该组试验只需第一轮注射的概率（用含 $p$ 的多项式表示）；

(2)、记该组动物需要注射次数 $X$ 的数学期望为 $E (X)$ ，求证： $10 < E (X) < 10 (2 - p)$ ．

查看试题解析
22. 已知函数 $f (x) = \frac{1}{e^{x}} + a x$ ， $g (x) = \ln x + \frac{1}{x}$ ．

(1)、当 $x > 0$ ， $a \leq 0$ 时，求证： $f (x) < g (x)$ ；

(2)、当 $x > 0$ 时，若 $f (x) > g (x + 1)$ ，求实数 $a$ 的取值范围．

查看试题解析