江苏省连云港市2021届高三下学期数学期初调研考试试卷
试卷更新日期:2021-06-18 类型:开学考试
一、单选题
-
1. 若非空且互不相等的集合 , , 满足: , ,则 ( ).A、 B、 C、 D、2. 在复平面内,复数 对应的点位于( ).A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 2月18日至28日在张家口举办国际雪联自由式滑雪和单板滑雪世界锦标赛.现组委会要从小张、小赵、小李、小罗、小王五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作,若其中小张和小赵只能从事前两项工作,其余三人均能从事这四项工作,则不同的选派方案的种数为( ).A、12 B、24 C、36 D、484. 已知双曲线 的右焦点到其一条渐近线的距离为 ,则双曲线的离心率为( ).A、 B、 C、 D、25. 的展开式中 的系数为( ).A、16 B、18 C、20 D、246. 函数 的部分图象大致为( ).A、
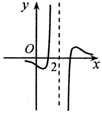 B、
B、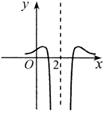 C、
C、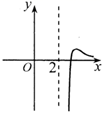 D、
D、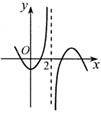 7. 中长跑是一项对学生身体锻炼价值较高的运动项目.在某校的一次中长跑比赛中,全体参赛学生的成绩近似地服从正态分布 ,已知成绩在90分以上(含90分)的学生有32名.则参赛的学生总数约为( ).(参考数据: , , )A、208 B、206 C、204 D、2028. 定义方程 的实数根 叫作函数 的“保值点”.如果函数 与函数 的“保值点”分别为 , ,那么 和 的大小关系是( )A、 B、 C、 D、无法确定9. 甲、乙、丙、丁四人参加数学竞赛,四人在成绩公布前作出如下预测:
7. 中长跑是一项对学生身体锻炼价值较高的运动项目.在某校的一次中长跑比赛中,全体参赛学生的成绩近似地服从正态分布 ,已知成绩在90分以上(含90分)的学生有32名.则参赛的学生总数约为( ).(参考数据: , , )A、208 B、206 C、204 D、2028. 定义方程 的实数根 叫作函数 的“保值点”.如果函数 与函数 的“保值点”分别为 , ,那么 和 的大小关系是( )A、 B、 C、 D、无法确定9. 甲、乙、丙、丁四人参加数学竞赛,四人在成绩公布前作出如下预测:甲预测说:我不会获奖,丙获奖; 乙预测说:甲和丁中有一人获奖;
丙预测说:甲的猜测是对的; 丁预测说:获奖者在甲、乙、丙三人中.
成绩公布后表明,四人的预测中有两人的预测与结果相符,另外两人的预测与结果不符已知有两人获奖,则获奖者可能是( ).
A、甲和乙 B、乙和丙 C、甲和丙 D、乙和丁二、多选题
-
10. 已知函数 在 有且仅有4个零点,则( ).A、 在 单调递增 B、 的取值范围是 C、 在 有2个极小值点 D、 在 有3个极大值点11. 如图,直三棱柱 中, , , 是棱 的中点, .则( ).
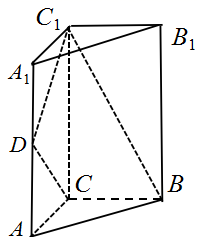 A、直线 与 所成角为 B、三棱锥 的体积为 C、二面角 的大小为 D、直三棱柱 外接球的表面积为12. 已知函数 ,则( ).A、 是奇函数 B、 C、 在 单调递增 D、 在 上存在一个极值点
A、直线 与 所成角为 B、三棱锥 的体积为 C、二面角 的大小为 D、直三棱柱 外接球的表面积为12. 已知函数 ,则( ).A、 是奇函数 B、 C、 在 单调递增 D、 在 上存在一个极值点三、填空题
-
13. 已知 , , ,则 .14. 一台设备由三个部件构成,假设在一天的运转中,部件1,2,3需要调整的概率分别为0.1,0.2,0.3,各部件的状态相互独立,则设备在一天的运转中,至少有1个部件需要调整的概率为.15. 写出一个满足 的偶函数 .16. 焦点为 的抛物线 上一点 , ,若以 为直径的圆过点 ,则圆心坐标为 , 抛物线的方程为.
四、解答题
-
17. 在① ,② ,③ 这三个条件中任选一个,补充在下面问题中,并完成解答.问题:已知等差数列 的前 项和为 , , ▲ , 若数列 满足 ,求数列 的前 项和 .18. 在 中,角 , , 所对的边分别为 , , ,已知 ,且 .(1)、证明: ;(2)、若 的周长为 ,求其面积 .19. 机动车行经人行横道时,应当减速慢行:遇行人正在通过人行横道,应当停车让行,俗称“礼让行人”.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员不“礼让行人”行为统计数据:
月份
1
2
3
4
5
违章驾驶员人数
120
105
100
95
80
(1)、请利用所给数据求违章人数 与月份 之间的回归直线方程 ;(2)、预测该路口9月份的不“礼让行人”违章驾驶员人数;(3)、交警从这5个月内通过该路口的驾驶员中随机抽查70人,调查驾驶员不“礼让行人”行为与驾龄的关系,得到下表:不礼让行人
礼让行人
驾龄不超过1年
24
16
驾龄1年以上
16
14
能否据此判断有97.5%的把握认为“礼让行人行为与驾龄有关?
参考公式: , .
(其中 )
P(x2≥k)
0.15
0.10
0.05
0.025
0.010
k
2.072
2.706
3.841
5.024
6.635