江苏省常州市2021届高三下学期数学学业水平监测期初联考试卷
试卷更新日期:2021-06-18 类型:开学考试
一、单选题
-
1. 已知集合 , ,若 ,则实数a的取值范围为( )A、 B、 C、 D、2. i是虚数单位,在复平面内复数 对应的点的坐标为( )A、( , ) B、( , ) C、( , ) D、( , )3. 已知a,b,c是实数,则“a≥b”是“ac2≥bc2”的( )A、充要条件 B、充分不必要条件 C、必要不充分条件 D、既不充分又不必要条件4. 设函数 ,若函数 的图象在点(1, )处的切线方程为y=x,则函数 的增区间为( )A、(0,1) B、(0, ) C、( , ) D、( ,1)5. 用红,黄,蓝,绿,黑这5种颜色随机给如图所示的四块三角形区域涂色,则“在任意两个有公共边的三角形所涂颜色不同”的概率为( )
 A、 B、 C、 D、6. 如果在一次实验中,测得(x,y)的四组数值分别是(1,2.2),(2,3.3),(4,5.8),(5,6.7),则y对x的线性回归方程是( )A、 B、 C、 D、7. 令 ( ) ,则 =( )A、 B、 C、 D、8. 函数 ,A>0, >0,k,b R,则函数 在区间(﹣ , )上的零点最多有( )A、4个 B、5个 C、6个 D、7个
A、 B、 C、 D、6. 如果在一次实验中,测得(x,y)的四组数值分别是(1,2.2),(2,3.3),(4,5.8),(5,6.7),则y对x的线性回归方程是( )A、 B、 C、 D、7. 令 ( ) ,则 =( )A、 B、 C、 D、8. 函数 ,A>0, >0,k,b R,则函数 在区间(﹣ , )上的零点最多有( )A、4个 B、5个 C、6个 D、7个二、多选题
-
9. 已知 , 是平面上夹角为 的两个单位向量, 在该平面上,且( ﹣ )·( ﹣ )=0,则下列结论中正确的有( )A、 B、 C、 D、 , 的夹角是钝角10. 已知在数学测验中,某校学生的成绩服从正态分布 ,其中90分为及格线,则下列结论中正确的有(附:随机变量 服从正态分布 ,则 )( )A、该校学生成绩的期望为110 B、该校学生成绩的标准差为9 C、该校学生成绩的标准差为81 D、该校学生成绩及格率超过95%11. 意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一列数:1,1,2,3,5,…,其中从第三项起,每个数等于它前面两个数的和,后来人们把这样的一列数组成的数列 称为“斐波那契数列”,记 为数列 的前n项和,则下列结论中正确的有( )A、 B、 C、 D、12. 设函数 的定义域为D,若存在常数a满足[﹣a,a] D,且对任意的 [﹣a,a],总存在 [﹣a,a],使得 ,称函数 为P(a)函数,则下列结论中正确的有( )A、函数 是 函数 B、函数 是 函数 C、若函数 是 函数,则t=4 D、若函数 是P( )函数,则b=
三、填空题
-
13. 圆柱上、下底面的圆周都在一个体积为 的球面上,圆柱底面直径为8,则该圆柱的表面积为.14. 函数 的最小正周期T=.15. 已知函数 ,则使不等式 成立的实数t的取值范围是.16. 已知椭圆C1: 的右焦点F也是抛物线C2:y2=nx的焦点,且椭圆与抛物线的交点到F的距离为 ,则实数n= , 椭圆C1的离心率e=.
四、解答题
-
17. 设等比数列 的公比为q(q≠1),前n项和为 .(1)、若 , ,求 的值;(2)、若q>1, ,且 ,m ,求m的值.18. 已知 中,它的内角 的对边分别为 ,且 .(1)、求 的值;(2)、若 ,求 的值.19. 已知某射手射中固定靶的概率为 ,射中移动靶的概率为 ,每次射中固定靶、移动靶分别得1分、2分,脱靶均得0分,每次射击的结果相互独立,该射手进行3次打靶射击:向固定靶射击1次,向移动靶射击2次.(1)、求“该射手射中固定靶且恰好射中移动靶1次”的概率;(2)、求该射手的总得分X的分布列和数学期望.20. 如图,在四棱锥 中,底面四边形 是矩形, ,平面 平面 ,二面角 的大小为 .
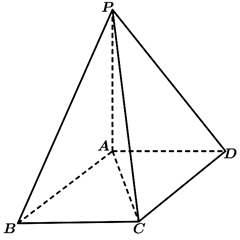 (1)、求证: 平面 ;(2)、求直线 与平面 所成的角的正弦值.
(1)、求证: 平面 ;(2)、求直线 与平面 所成的角的正弦值.