山东省枣庄市薛城区2020-2021学年七年级下学期数学期中试卷
试卷更新日期:2021-06-18 类型:期中考试
一、单选题
-
1. 下列运算正确的是( )A、 B、a6÷a2=a3 C、5y3•3y2=15y5 D、a+a2=a32. 如图,直线a,b被直线c所截,下列条件中,不能判定a∥b( )
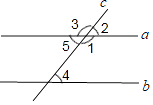 A、∠2=∠4 B、∠1+∠4=180° C、∠5=∠4 D、∠1=∠33. 若(x-2y)2 =(x+2y)2+M,则M= ( )A、4xy B、- 4xy C、8xy D、-8xy4. 如图所示,下列说法错误的是( )
A、∠2=∠4 B、∠1+∠4=180° C、∠5=∠4 D、∠1=∠33. 若(x-2y)2 =(x+2y)2+M,则M= ( )A、4xy B、- 4xy C、8xy D、-8xy4. 如图所示,下列说法错误的是( )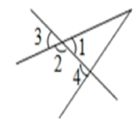 A、∠1和∠2是同旁内角 B、∠1和∠3是对顶角 C、∠3和∠4是同位角 D、∠1和∠4是内错角5. 如图,直线AB、CD相交于点O,射线OM平分∠AOC,∠MON=90°.若∠AOM=35°,则∠CON的度数为( )
A、∠1和∠2是同旁内角 B、∠1和∠3是对顶角 C、∠3和∠4是同位角 D、∠1和∠4是内错角5. 如图,直线AB、CD相交于点O,射线OM平分∠AOC,∠MON=90°.若∠AOM=35°,则∠CON的度数为( ) A、35° B、45° C、55° D、65°6. 下列各式中,计算结果正确的是( )A、 B、 C、 D、7. 在某次试验中,测得两个变量m和v之间的4组对应数据如下表:
A、35° B、45° C、55° D、65°6. 下列各式中,计算结果正确的是( )A、 B、 C、 D、7. 在某次试验中,测得两个变量m和v之间的4组对应数据如下表:1
2
3
4
0.01
2.9
8.03
15.1
则m与v之间的关系最接近于下列各关系式中的 ( )
A、 B、 C、 D、8. 已知|x+y+5|+(xy﹣6)2=0,则x2+y2的值等于( )A、1 B、13 C、17 D、259. 下列说法正确的个数是( )①对顶角相等;
②等角的补角相等;
③两直线平行,同旁内角相等;
④在同一平面内,过一点有且只有一条直线与已知直线垂直
A、1 B、2 C、3 D、410. 若两个角的一边在同一条直线上,另一边相互平行,那么这两个角的关系是( )A、相等 B、互补 C、相等或互补 D、不能确定11. 如果 x2﹣kx﹣ab=(x﹣a)(x+b),则k应为( )A、a﹣b B、a+b C、b﹣a D、﹣a﹣b12. 如图①,在长方形 中,动点P从点B出发,沿 , , 运动至点A停止,设点P运动的路程为x, 的面积为y,如果y与x之间的图象如图②所示,则长方形 的面积是( )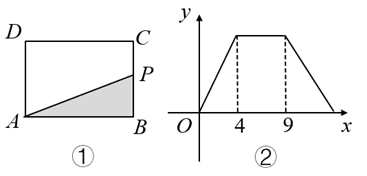 A、10 B、16 C、20 D、36
A、10 B、16 C、20 D、36二、填空题
-
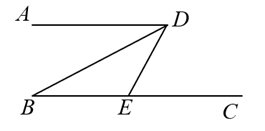
13. 已知某新型感冒病毒的直径约为0.000000823米,将0.000000823用科学记数法表示为14. 计算 .15. 如图,已知 , , 平分 ,则 .
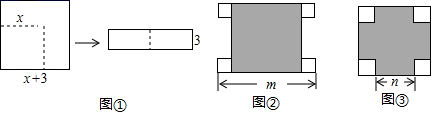
 16. 已知(2x2﹣3x+a)(x+2)计算结果中不含x项,则a= .17. 点燃一根蜡烛后,蜡烛的高度h(厘米)与燃烧时间t(分)之间的关系如下表:
16. 已知(2x2﹣3x+a)(x+2)计算结果中不含x项,则a= .17. 点燃一根蜡烛后,蜡烛的高度h(厘米)与燃烧时间t(分)之间的关系如下表:t/分
0
2
4
6
8
10
h/厘米
30
29
28
27
26
25
写出蜡烛的高度h(厘米)与燃烧时间t(分)之间的关系式;这根蜡烛最多能燃烧的时间为分.
18. 已知 , ,则 .三、解答题
-
19. 如图,某村庄计划把河中的水引到水池M中,怎样开的渠最短,为什么(保留作图痕迹,不写作法和证明)
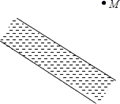
理由是: .
20. 计算:(1)、(3x2)2•(﹣4y3)÷(6xy)2;(2)、[(2x﹣y)(2x+y)+y(y﹣6x)]÷2x.21. 先化简,再求值:(2a﹣b)2﹣(a+1﹣b)(a+1+b)+(a+1)2 , 其中a= ,b=﹣2.22. 如图,已知AB∥CD,FG∥HD,∠D=42°,EF为∠CEB的平分线,求∠B的度数.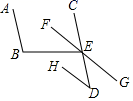 23. 将长为 的长方形白纸,按图中的方法粘合起来,粘合部分的宽为 .
23. 将长为 的长方形白纸,按图中的方法粘合起来,粘合部分的宽为 .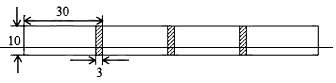 (1)、求5张白纸粘合后的长度.(2)、设x张白纸粘合后的长度为 ,写出y与x之间的关系式.并求当 时,y的值.24. 阅读第(1)题解答过程填理由,并解答第(2)题(1)、已知:如图1,AB∥CD,P为AB,CD之间一点,求∠B+∠C+∠BPC的大小.
(1)、求5张白纸粘合后的长度.(2)、设x张白纸粘合后的长度为 ,写出y与x之间的关系式.并求当 时,y的值.24. 阅读第(1)题解答过程填理由,并解答第(2)题(1)、已知:如图1,AB∥CD,P为AB,CD之间一点,求∠B+∠C+∠BPC的大小.
解:过点P作PM∥AB
∵AB∥CD(已知)
∴PM∥CD ▲ ,
∴∠B+∠1=180°, ▲ .
∴∠C+∠2=180° ▲ .
∵∠BPC=∠1+∠2
∴∠B+∠C+∠BPC=360°
(2)、我们生活中经常接触小刀,如图2小刀刀柄外形是一个直角梯形挖去一个小半圈,其中AF∥EG,∠AEG=90°,刀片上、下是平行的(AB∥CD),转动刀片时会形成∠1和∠2,那么∠1+∠2的大小是否会随刀片的转动面改变,如不改变,求出其大小;如改变,请说明理由. 25. 在乘法公式的学习中,我们采用了构造几何图形的方法研究问题,借助直观、形象的几何模型,加深对乘法公式的认识和理解,从中感悟数形结合的思想方法,感悟几何与代数内在的统一性,根据课堂学习的经验,解决下列问题:(1)、如图①边长为(x+3)的正方形纸片,剪去一个边长为x的正方形之后,剩余部分可拼剪成一个长方形(不重叠无缝隙),则这个长方形的面积为(用含x的式子表示).(2)、如果你有5张边长为a的正方形纸,4张长、宽分别为a、b(a>b)的长方形纸片,3张边长为b正方形纸片.现从其中取出若干张纸片,每种纸片至少取一张,把取出的这些纸片拼成一个正方形(不重叠无缝隙),则拼成的正方形的边长最长可以为
25. 在乘法公式的学习中,我们采用了构造几何图形的方法研究问题,借助直观、形象的几何模型,加深对乘法公式的认识和理解,从中感悟数形结合的思想方法,感悟几何与代数内在的统一性,根据课堂学习的经验,解决下列问题:(1)、如图①边长为(x+3)的正方形纸片,剪去一个边长为x的正方形之后,剩余部分可拼剪成一个长方形(不重叠无缝隙),则这个长方形的面积为(用含x的式子表示).(2)、如果你有5张边长为a的正方形纸,4张长、宽分别为a、b(a>b)的长方形纸片,3张边长为b正方形纸片.现从其中取出若干张纸片,每种纸片至少取一张,把取出的这些纸片拼成一个正方形(不重叠无缝隙),则拼成的正方形的边长最长可以为A.a+b;B.a+2b;C.a+3b;D.2a+b.
(3)、1个大正方形和4个大小完全相同的小正方形按图②③两种方式摆放,求图③中,大正方形中未被4个小正方形覆盖部分的面积.(用含m、n的代数式表示)