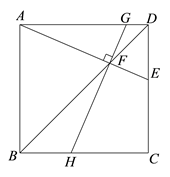山东省威海乳山市(五四制)2020-2021学年九年级下学期数学期中试卷
试卷更新日期:2021-06-18 类型:期中考试
一、单选题
-
1. 熔喷布,俗称口罩的“心脏”,是口罩中间的过滤层,能过滤细菌,阻止病菌传播.经测量,医用外科口罩的熔喷布厚度约为0.000156米,将0.000156用科学记数法表示应为( )A、 B、 C、 D、2. 下面计算正确的是( )A、 B、 C、 D、3. 如图,在 中, , 平分 ,且 ,则 的度数为( )
 A、70° B、60° C、50° D、40°4. 如果 ,那么代数式 的值为( )A、12 B、6 C、2 D、-65. 如图,△ABC内接于⊙O , 若∠A=45°,OC=2,则BC的长为( )
A、70° B、60° C、50° D、40°4. 如果 ,那么代数式 的值为( )A、12 B、6 C、2 D、-65. 如图,△ABC内接于⊙O , 若∠A=45°,OC=2,则BC的长为( ) A、 B、 C、 D、46. 《九章算术》是中国古代重要的数学著作,其中“盈不足术”记载:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数鸡价各几何?译文:今有人合伙买鸡,每人出九钱,会多出11钱;每人出6钱,又差16钱.问人数、买鸡的钱数各是多少?设人数为 ,买鸡的钱数为 ,可列方程组为( )A、 B、 C、 D、7. 如图,在 中,延长 至点E,使 ,连接 交 于点F,交 于点G,则 的值是( )
A、 B、 C、 D、46. 《九章算术》是中国古代重要的数学著作,其中“盈不足术”记载:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数鸡价各几何?译文:今有人合伙买鸡,每人出九钱,会多出11钱;每人出6钱,又差16钱.问人数、买鸡的钱数各是多少?设人数为 ,买鸡的钱数为 ,可列方程组为( )A、 B、 C、 D、7. 如图,在 中,延长 至点E,使 ,连接 交 于点F,交 于点G,则 的值是( ) A、 B、 C、 D、8. 如图,正比例函数 的图象和反比例函数 的图象交于 两点,分别过点 作 轴的垂线,垂足为 ,则 与 的面积之和为( )
A、 B、 C、 D、8. 如图,正比例函数 的图象和反比例函数 的图象交于 两点,分别过点 作 轴的垂线,垂足为 ,则 与 的面积之和为( )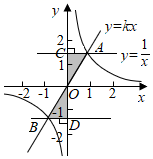 A、 B、 C、1 D、9. 如图1,点P从 的顶点A出发,沿A→C→B的路径匀速运动到点B停止,作PQ⊥AB于点Q,设点P运动的路程为x,PQ的长为y,若y与x之间的函数关系如图2所示,当x=6时,PQ的长为( )
A、 B、 C、1 D、9. 如图1,点P从 的顶点A出发,沿A→C→B的路径匀速运动到点B停止,作PQ⊥AB于点Q,设点P运动的路程为x,PQ的长为y,若y与x之间的函数关系如图2所示,当x=6时,PQ的长为( )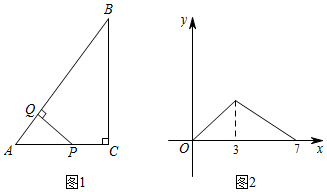 A、1 B、 C、 D、10. 如图,正六边形 的边长为6,点 为正六边形的中心,将半径为 的⊙M在正六边形的内部沿边逆时针滚动,连接 ,过点 作 ,并且 ,连接 ⊙M在滚动的过程中, 面积的最大值是( )
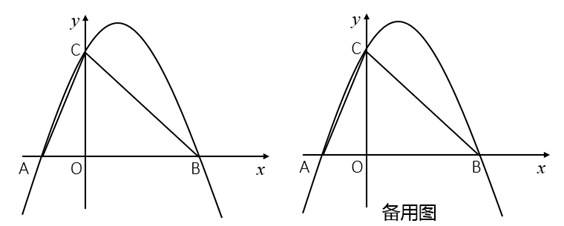
A、1 B、 C、 D、10. 如图,正六边形 的边长为6,点 为正六边形的中心,将半径为 的⊙M在正六边形的内部沿边逆时针滚动,连接 ,过点 作 ,并且 ,连接 ⊙M在滚动的过程中, 面积的最大值是( )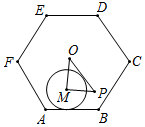 A、 B、 C、6 D、811. 一组数据为5,6,7,7,10,10,某同学在抄题的时候,误将其中的一个10抄成了16,那么该同学所抄的数据和原数据相比,不变的统计量是( )A、极差 B、平均数 C、中位数 D、众数12. 如图,抛物线 .将该抛物线在x轴和x轴下方的部分记作 ,将 沿x轴翻折记作 , 和 构成的图形记作 .关于图形 ,给出如下四个结论,其中错误的是( )
A、 B、 C、6 D、811. 一组数据为5,6,7,7,10,10,某同学在抄题的时候,误将其中的一个10抄成了16,那么该同学所抄的数据和原数据相比,不变的统计量是( )A、极差 B、平均数 C、中位数 D、众数12. 如图,抛物线 .将该抛物线在x轴和x轴下方的部分记作 ,将 沿x轴翻折记作 , 和 构成的图形记作 .关于图形 ,给出如下四个结论,其中错误的是( ) A、图形 恰好经过4个整点(即横、纵坐标均为整数的点) B、图形 上任意一点到原点的距离都不超过1 C、图形 的周长大于 D、图形 所围成的区域的面积大于2且小于
A、图形 恰好经过4个整点(即横、纵坐标均为整数的点) B、图形 上任意一点到原点的距离都不超过1 C、图形 的周长大于 D、图形 所围成的区域的面积大于2且小于二、填空题
-
13. 因式分解: .14. 将容量为100的样本分成3个组,第一组的频数是35,第二组的频率是0.28,那么第三组的频率是.15. 如图,O是▱ABCD的对称中心,点E在边BC上,AD=7,BE=3,将 绕点O旋转180°,设点E的对应点为 ,则 = .
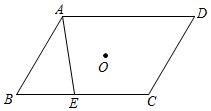 16. 已知关于 的一元二次方程 的两个实数根是 ,那么 的最大值是 .17. 如图,在菱形 中, 为 边上的高,将 沿 所在的直线翻折,得到 ,若 ,则菱形的边长为 .
16. 已知关于 的一元二次方程 的两个实数根是 ,那么 的最大值是 .17. 如图,在菱形 中, 为 边上的高,将 沿 所在的直线翻折,得到 ,若 ,则菱形的边长为 .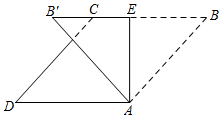 18. 如图,在平面直角坐标系中,边长为1的正方形 的顶点 分别在 轴, 轴上,点 在反比例函数 图象上,过 的中点 作矩形 ,使顶点 落在反比例函数 图象上,再过 的中点 作矩形 ,使顶点 落在反比例函数 图象上,…,依此规律,作出矩形 时,落在反比例函数 图象上的顶点 的坐标为 .
18. 如图,在平面直角坐标系中,边长为1的正方形 的顶点 分别在 轴, 轴上,点 在反比例函数 图象上,过 的中点 作矩形 ,使顶点 落在反比例函数 图象上,再过 的中点 作矩形 ,使顶点 落在反比例函数 图象上,…,依此规律,作出矩形 时,落在反比例函数 图象上的顶点 的坐标为 .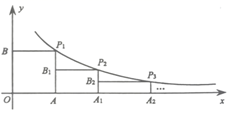
三、解答题
-
19. 解不等式组 ,并写出它的所有非负整数解 .20. 为落实“精致乳山”工作部署,市政府计划对城区道路进行改造.计划安排甲、乙两个工程队完成,已知甲队的工作效率是乙队工作效率的 倍,甲队改造720米的道路比乙队改造同样长的道路少用4天.甲、乙两工程队每天改造道路的长度分别是多少米?21. 为了解我市市民读党史书籍的情况,小明同学在自己小区内进行了抽样调查.他随机抽取了小区30户家庭,收集到的读党史书籍的本书如下(单位:本):1,1,2,3,2,3,2,3,3,4,3,3,4,3,3,5,3,4,3,4,4,5,4,5,3,4,3,4,5,6
通过数据进行整理,绘制了如下统计图:
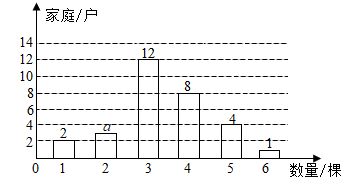
根据上述信息解决问题:
(1)、这30户家庭读党史书籍本书的众数是 , 中位数是;(2)、若绘制扇形统计图,则读4本书籍所在的扇形圆心角度数为°;(3)、要从读2本和读6本的家庭中,任意选取两个家庭采访小区居民对读党史书籍的认识,求恰好选中读2本和读6本党史数据的家庭的概率.22. 如图,一架无人机沿水平方向由 处飞行6千米到达 处,在航线 下方有两个山头 .无人机在 处,测得 的俯角分别为 和 .无人机在 处,测得 的俯角为 ,此时山头 恰好在无人机的正下方.求山头 之间的距离.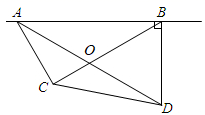 23. 如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,点O在射线 上(点 不与点 重合),过点 作 ,垂足为 ,以点 为圆心, 为半径画半圆 ,分别交射线 于 、 两点,设 .(1)、如图,当点 为 边的中点时,求 的值;
23. 如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,点O在射线 上(点 不与点 重合),过点 作 ,垂足为 ,以点 为圆心, 为半径画半圆 ,分别交射线 于 、 两点,设 .(1)、如图,当点 为 边的中点时,求 的值;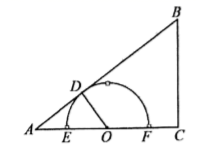 (2)、如图,当点 与点 重合时,连接 ,求弦 的长;
(2)、如图,当点 与点 重合时,连接 ,求弦 的长;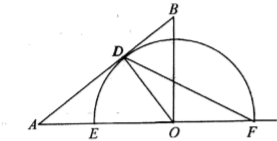 (3)、当半圆 与 无交点时,直接写出 的取值范围.
(3)、当半圆 与 无交点时,直接写出 的取值范围.