山东省菏泽市曹县2020-2021学年九年级下学期数学期中试卷
试卷更新日期:2021-06-18 类型:期中考试
一、单选题
-
1. 的相反数是( )A、2 B、4 C、-2 D、-42. 某种芯片每个探针单元的面积为 ,数据0.00000164用科学记数法表示为( )A、 B、 C、 D、3. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
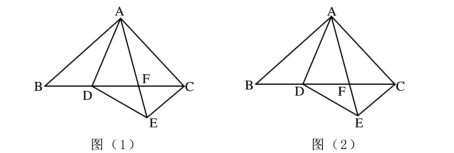
D、 4. 某校九年级模拟考试中,1班的六名学生的数学成绩如下:96,108,102,110,108,82.下列关于这组数据的描述错误的是( )A、众数是108 B、中位数是105 C、平均数是101 D、方差是935. 如图, 中, 平分 ,交 于点 , , , ,则 的长为( )
4. 某校九年级模拟考试中,1班的六名学生的数学成绩如下:96,108,102,110,108,82.下列关于这组数据的描述错误的是( )A、众数是108 B、中位数是105 C、平均数是101 D、方差是935. 如图, 中, 平分 ,交 于点 , , , ,则 的长为( )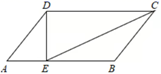 A、 B、 C、 D、6. 若点 , 在反比例函数 的图象上,且 ,则a的取值范围是( )A、 B、 C、 D、 或7. 如图,把 沿着 的方向平移到 的位置,它们重叠部分的面积是 面积的一半,若 ,则 移动的距离是( )
A、 B、 C、 D、6. 若点 , 在反比例函数 的图象上,且 ,则a的取值范围是( )A、 B、 C、 D、 或7. 如图,把 沿着 的方向平移到 的位置,它们重叠部分的面积是 面积的一半,若 ,则 移动的距离是( )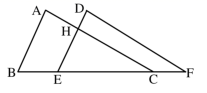 A、 B、 C、 D、8. 如图,在平面直角坐标系中,点 , , ,…, 在 轴上,点 , ,…, 在直线 上,若点 的坐标为 ,且 , ,…, 都是等边三角形,从左到右的小三角形(阴影部分)的面积分别记为 , ,.., ,则 可表示为( )
A、 B、 C、 D、8. 如图,在平面直角坐标系中,点 , , ,…, 在 轴上,点 , ,…, 在直线 上,若点 的坐标为 ,且 , ,…, 都是等边三角形,从左到右的小三角形(阴影部分)的面积分别记为 , ,.., ,则 可表示为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 计算 的结果是 .10. 已知圆锥的底面半径为 ,侧面展开图的圆心角是180°,则圆锥的高是 .11. 已知 ,则 .12. 如图,四边形 是菱形,对角线 , 相交于点 , , ,点 是 上一点,连接 ,若 ,则 的长为 .
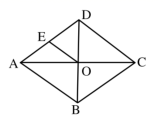 13. 如图,在平面直角坐标系中,点A、B的坐标分别为 、 ,点 在第一象限内,连接 、 .已知 ,则 .
13. 如图,在平面直角坐标系中,点A、B的坐标分别为 、 ,点 在第一象限内,连接 、 .已知 ,则 . 14. 如图,正方形 中, 绕点 逆时针旋转得到 , , 分别交对角线 于点 , ,若 ,则 的值为 .
14. 如图,正方形 中, 绕点 逆时针旋转得到 , , 分别交对角线 于点 , ,若 ,则 的值为 .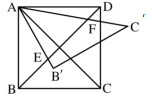
三、解答题
-
15. 如图,在 中,以 为直径作 交 于点 ,交 于点 ,点 是 的中点,过点 作 的切线,交 于点 ,交 的延长线于点 .
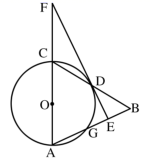 (1)、求证: ;(2)、若 , ,求 的长.16. 计算: .17. 解不等式组:18. 如图,点 在 的边 上,以 为半径作 , 的平分线 交 于点 ,过点 作 于点 ,使用直尺和圆规补全图形(不写作法,保留作图痕迹).
(1)、求证: ;(2)、若 , ,求 的长.16. 计算: .17. 解不等式组:18. 如图,点 在 的边 上,以 为半径作 , 的平分线 交 于点 ,过点 作 于点 ,使用直尺和圆规补全图形(不写作法,保留作图痕迹).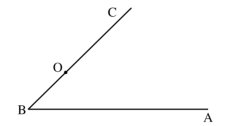 19. 如图,这是某水库大坝截面示意图,张强在水库大坝顶CF上的瞭望台D处,测得水面上的小船A的俯角为40°,若DE=3米,CE=2米,CF平行于水面AB,瞭望台DE垂直于坝顶CF,迎水坡BC的坡度i=4:3,坡长BC=10米,求小船A距坡底B处的长.(结果保留0.1米)(参考数据:sin40°≈0.64,cos40°=0.77,tan40°≈0.84)
19. 如图,这是某水库大坝截面示意图,张强在水库大坝顶CF上的瞭望台D处,测得水面上的小船A的俯角为40°,若DE=3米,CE=2米,CF平行于水面AB,瞭望台DE垂直于坝顶CF,迎水坡BC的坡度i=4:3,坡长BC=10米,求小船A距坡底B处的长.(结果保留0.1米)(参考数据:sin40°≈0.64,cos40°=0.77,tan40°≈0.84)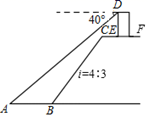 20. 第5代移动通信技术简称5G , 某地已开通5G业务,经测试5G下载速度是4G下载速度的15倍,小明和小强分别用5G与4G下载一部600兆的公益片,小明比小强所用的时间快140秒,求该地4G与5G的下载速度分别是每秒多少兆?21. 如图,一次函数的图象与反比例函数的图象相交于 , 两点,与 轴的正半轴相交于点 ,与 轴的负半轴交于点 , , .
20. 第5代移动通信技术简称5G , 某地已开通5G业务,经测试5G下载速度是4G下载速度的15倍,小明和小强分别用5G与4G下载一部600兆的公益片,小明比小强所用的时间快140秒,求该地4G与5G的下载速度分别是每秒多少兆?21. 如图,一次函数的图象与反比例函数的图象相交于 , 两点,与 轴的正半轴相交于点 ,与 轴的负半轴交于点 , , .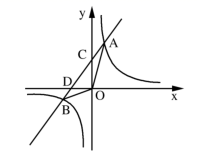 (1)、求反比例的表达式;(2)、若点 的横坐标为 ,求 的面积.22. 某校“演讲比赛”结束后,将所有参赛选手的比赛成绩(得分均为整数)进行整理,并绘制成扇形统计图和频数分布直方图.
(1)、求反比例的表达式;(2)、若点 的横坐标为 ,求 的面积.22. 某校“演讲比赛”结束后,将所有参赛选手的比赛成绩(得分均为整数)进行整理,并绘制成扇形统计图和频数分布直方图.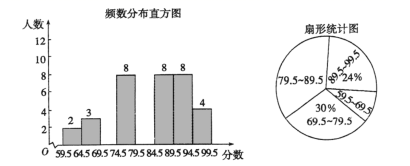 (1)、求本次比赛参赛的选手共有多少人?(2)、赛前规定,成绩由高到底前40%的参赛选手获奖,某选手的比赛成绩为88分,试判断他能否获奖?并说明理由.(3)、成绩前4名是1名男生和3名女生,若从他们中任选2人参加上一级的比赛,求恰好选中1男生和l女生的概率.
(1)、求本次比赛参赛的选手共有多少人?(2)、赛前规定,成绩由高到底前40%的参赛选手获奖,某选手的比赛成绩为88分,试判断他能否获奖?并说明理由.(3)、成绩前4名是1名男生和3名女生,若从他们中任选2人参加上一级的比赛,求恰好选中1男生和l女生的概率.