安徽省皖南八校2020-2021学年高三上学期理数摸底联考试卷
试卷更新日期:2021-06-18 类型:开学考试
一、单选题
-
1. 已知全集 ,集合 , ,则 ( )A、 B、 C、 D、2. 已知命题 , 是增函数,则 为( )A、 , 是减函数 B、 , 是增函数 C、 , 不是增函数 D、 , 不是增函数3. 已知双曲线 的两条渐近线互相垂直,且焦距为 ,则抛物线 的准线方程为( )A、 B、 C、 D、4. 已知向量 , ,若 ,则 ( )A、10 B、2 C、 D、5. 将函数 的图象向左平移 个周期后,所得图象对应的函数为( )A、 B、 C、 D、6. 我国古代数学著作《算法统宗》中有这样一个问题(意为):“有一个人要走378里路,第一天健步行走,从第二天起因脚痛每天走的路程为前一天的一半,走了6天后到达目的地.”那么,此人第3天和第4天共走路程是( )A、72里 B、60里 C、48里 D、36里7. 执行如下的程序框图,为使输出的b的值为16,则循环体的判断框内①处应开始填的整数为( )
 A、3 B、4 C、5 D、68. 函数y= sin2x的图象可能是( )
A、3 B、4 C、5 D、68. 函数y= sin2x的图象可能是( )
A、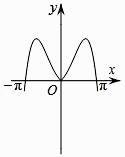 B、
B、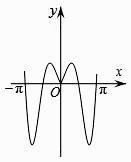 C、
C、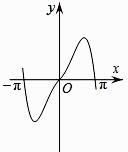 D、
D、 9. 若正实数x , y满足 ,则 的最小值为( )A、 B、 C、12 D、410. 某空间几何体的三视图如图所示,则该几何体中直线 (点B为俯视图中矩形的中心)与平面 所成角的余弦值为( )
9. 若正实数x , y满足 ,则 的最小值为( )A、 B、 C、12 D、410. 某空间几何体的三视图如图所示,则该几何体中直线 (点B为俯视图中矩形的中心)与平面 所成角的余弦值为( ) A、 B、 C、 D、11. 已知函数 满足 ,若函数 与 图象的交点为 ,则交点的所有横坐标和纵坐标之和为( )A、1010 B、-2020 C、2020 D、404012. 若曲线 在点 处的切线过点 ,则函数 的单调递减区间为( )A、 B、 C、 D、 ,
A、 B、 C、 D、11. 已知函数 满足 ,若函数 与 图象的交点为 ,则交点的所有横坐标和纵坐标之和为( )A、1010 B、-2020 C、2020 D、404012. 若曲线 在点 处的切线过点 ,则函数 的单调递减区间为( )A、 B、 C、 D、 ,二、填空题
-
13. 已知复数z满足: ,则 .14. 已知点M的坐标 满足不等式组 , 为直线 上任一点,则 的最小值是15. 已知等差数列 的公差d不为0,等比数列 的公比 ,若 , , 是正整数,则实数 .16. 已知偶函数 满足 ,且当 时, ,若在区间 内,函数 有且仅有3个零点,则实数k的取值范围是.
三、解答题
-
17. 在三角形 中,已知角A , B , C的对边分别为a , b , c , 且 .(1)、求角B的大小;(2)、若 ,求三角形 面积的最大值.18. 已知等差数列 的公差为 ,等差数列 的公差为 ,设 , 分别是数列 , 的前 项和,且 , , .(1)、求数列 , 的通项公式;(2)、设 ,数列 的前 项和为 ,证明: .19. 如图,在三棱柱 中, 是边长为2的等边三角形,平面 平面 ,四边形 为菱形, , 与 相交于点D.
 (1)、求证: .(2)、求平面 与平面 所成锐二面角的余弦值.20. 某工厂生产了一批零件,从中随机抽取100个作为样本,测出它们的长度(单位:厘米),按数据分成 , , , , 5组,得到如图所示的频率分布直方图.以这100个零件的长度在各组的频率代替整批零件长度在该组的概率.
(1)、求证: .(2)、求平面 与平面 所成锐二面角的余弦值.20. 某工厂生产了一批零件,从中随机抽取100个作为样本,测出它们的长度(单位:厘米),按数据分成 , , , , 5组,得到如图所示的频率分布直方图.以这100个零件的长度在各组的频率代替整批零件长度在该组的概率. (1)、估计该工厂生产的这批零件长度的平均值(同一组中的每个数据用该组区间的中点值代替);(2)、若用分层抽样的方式从第1组和第5组中抽取5个零件,再从这5个零件中随机抽取2个,求抽取的零件中恰有1个是第1组的概率.
(1)、估计该工厂生产的这批零件长度的平均值(同一组中的每个数据用该组区间的中点值代替);(2)、若用分层抽样的方式从第1组和第5组中抽取5个零件,再从这5个零件中随机抽取2个,求抽取的零件中恰有1个是第1组的概率.