2017-2021年高考数学全国甲卷（原全国卷3）三角函数与解三角形汇编（文理）

试卷更新日期：2021-06-18 类型：二轮复习

进入出卷网下载

一、单选题

1. 在 $△ A B C$ 中，已知 $B ＝ 120^{\circ} ， A C ＝ \sqrt{19} ， A B ＝ 2$ ，则 $B C ＝$ （）

A、1 B、 $\sqrt{2}$ C、 $\sqrt{5}$ D、3

查看试题解析
2. 2020年12月8日，中国和尼泊尔联合公布珠穆朗玛峰最新高程为8848.86（单位：m），三角高程测量法是珠峰高程测量方法之一.右图是三角高程测量法的一个示意图，现有以A，B，C三点，且A，B，C在同一水平而上的投影A’，B’，C'满足 $∠ A^{'} C^{'} B = 45 ° ， ∠ A^{'} B^{'} C^{'} = 60 °$ .由c点测得B点的仰角为15°，曲， $B B^{'}$ 与 $C C^{'}$ 的差为100 ：由B点测得A点的仰角为45°，则A，C两点到水平面 $A^{'} B^{'} C^{'}$ 的高度差 $A A^{'} - C C^{'}$ 约为（） $（ \sqrt{3} \approx 1.732 ）$

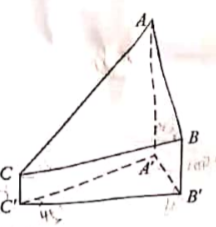A、346 B、373 C、446 D、473

查看试题解析
3. 若 $α \in （ 0, \frac{π}{2})$ , $\tan 2 α = \frac{\cos α}{2 - \sin α}$ ，则 $\tan α =$ （）

A、 $\frac{\sqrt{15}}{15}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{\sqrt{5}}{3}$ D、 $\frac{\sqrt{15}}{3}$

查看试题解析
4. 在△ABC中，cosC= $\frac{2}{3}$ ，AC=4，BC=3，则tanB=（）

A、 $\sqrt{5}$ B、2 $\sqrt{5}$ C、4 $\sqrt{5}$ D、8 $\sqrt{5}$

查看试题解析
5. 已知 $\sin θ + \sin (θ + \frac{π}{3}) = 1$ ，则 $\sin (θ + \frac{π}{6}) =$ （）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{2}{3}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析
6. 在△ABC中，cosC= $\frac{2}{3}$ ，AC=4，BC=3，则cosB=（）

A、 $\frac{1}{9}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
7. 已知2tanθ–tan(θ+ $\frac{π}{4}$ )=7，则tanθ=（）

A、–2 B、–1 C、1 D、2

查看试题解析
8. 设函数f（x）=sin（ωx+ $\frac{π}{5}$ ）（ω>0），已如f（x）在[0，2π]有且仅有5个零点，下述四个结论：①f（x）在（0，2π）有且仅有3个极大值点②f（x）在（0，2π）有且仅有2个极小值点③f（x）在（0， $\frac{π}{10}$ ）单调递增④ω的取值范围[ $\frac{12}{5}$ ， $\frac{29}{10}$ ）其中所有正确结论的编号是（）

A、①④ B、②③ C、①②③ D、①③④

查看试题解析
9. $Δ A B C$ 的内角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ，若 $Δ A B C$ 的面积为 $\frac{a^{2} + b^{2} - c^{2}}{4}$ ，则 $C$ =（）

A、 $\frac{π}{2}$ B、 $\frac{π}{3}$ C、 $\frac{π}{4}$ D、 $\frac{π}{6}$

查看试题解析
10. 若 $\sin α = \frac{1}{3}$ ，则 $\cos 2 α$ =（）

A、 $\frac{8}{9}$ B、 $\frac{7}{9}$ C、- $\frac{7}{9}$ D、- $\frac{8}{9}$

查看试题解析
11. 设函数f（x）=cos（x+ $\frac{π}{3}$ ），则下列结论错误的是（）

A、f（x）的一个周期为﹣2π B、y=f（x）的图象关于直线x= $\frac{8 π}{3}$ 对称 C、f（x+π）的一个零点为x= $\frac{π}{6}$ D、f（x）在（ $\frac{π}{2}$ ，π）单调递减

查看试题解析
12. 已知sinα﹣cosα= $\frac{4}{3}$ ，则sin2α=（　　）

A、﹣ $\frac{7}{9}$ B、﹣ $\frac{2}{9}$ C、 $\frac{2}{9}$ D、 $\frac{7}{9}$

查看试题解析
13. 函数f（x）= $\frac{1}{5}$ sin（x+ $\frac{π}{3}$ ）+cos（x﹣ $\frac{π}{6}$ ）的最大值为（　　）

A、 $\frac{6}{5}$ B、1 C、 $\frac{3}{5}$ D、 $\frac{1}{5}$

查看试题解析
14. 若tanα= $\frac{3}{4}$ ，则cos²α+2sin2α=（　　）

A、 $\frac{64}{25}$ B、 $\frac{48}{25}$ C、1 D、 $\frac{16}{25}$

查看试题解析
15. 在△ABC中，B= $\frac{π}{4}$ ，BC边上的高等于 $\frac{1}{3}$ BC，则cosA=（　　）

A、 $\frac{3 \sqrt{10}}{10}$ B、 $\frac{\sqrt{10}}{10}$ C、﹣ $\frac{\sqrt{10}}{10}$ D、﹣ $\frac{3 \sqrt{10}}{10}$

查看试题解析

二、填空题

16. 已知函数 $f (x) = 2 \cos (ωx + φ)$ 的部分图像如图所示，则满足条件 $（ f (x) - f (- \frac{7 π}{4})) (f (x) - f (\frac{4 π}{3})) > 0$ 的最小正整数x为。

查看试题解析
17. 关于函数f（x）= $\sin x + \frac{1}{\sin x}$ 有如下四个命题：
①f（x）的图像关于y轴对称．

②f（x）的图像关于原点对称．

③f（x）的图像关于直线x= $\frac{π}{2}$ 对称．

④f（x）的最小值为2．

其中所有真命题的序号是．

查看试题解析
18. 函数 $f (x) = \cos (3 x + \frac{π}{6})$ 在 $[0 ， π)$ 的零点个数为．

查看试题解析
19. △ABC的内角A，B，C的对边分别为a，b，c，已知C=60°，b= $\sqrt{6}$ ，c=3，则A= ．

查看试题解析

三、解答题

20. △ABC的内角A、B、C的对边分别为a，b，c，已知 $a \sin \frac{A + C}{2} = b \sin A$

(1)、求B；

(2)、若△ABC为锐角三角形，且c=1，求△ABC面积的取值范围.

查看试题解析
21. △ABC的内角A，B，C的对边分别为a，b，c，已知sinA+ $\sqrt{3}$ cosA=0，a=2 $\sqrt{7}$ ，b=2．
（Ⅰ）求c；
（Ⅱ）设D为BC边上一点，且AD⊥AC，求△ABD的面积．

查看试题解析