安徽省十校联盟2021届高三下学期理数开学考试试卷
试卷更新日期:2021-06-17 类型:开学考试
一、单选题
-
1. 已知集合 , ,则 的真子集个数为( )A、3 B、4 C、7 D、82. 若纯虚数 满足 ,则实数 的值为( )A、 B、 C、 D、3. “共享单车,绿色出行”是近年来火爆的广告词,现对某市10名共享单车用户一个月内使用共享单车的次数进行统计,得到数据如下所示,下列关于该组数据的说法错误的是( )
 A、极差为36 B、众数为34 C、中位数为27 D、平均数为324. “ ”是“函数 在 上单调递增”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 若 ,则 ( )A、-7 B、7 C、 D、6. 已知 , , ,则( )A、 B、 C、 D、7. 已知抛物线 的焦点为F,准线为l,过抛物线上一点P作 ,垂足为Q,若 ,则 ( )A、 B、 C、 D、8. 2020年是全面建成小康社会的目标实现之年,也是全面打赢脱贫攻坚战的收官之年.为更好地将“精准扶贫”落到实处,某地安排7名干部(3男4女)到三个贫困村调研走访,每个村安排男、女干部各1名,剩下1名干部负责统筹协调,则不同的安排方案有( )A、72种 B、108种 C、144种 D、210种9. 已知正方体 的棱长为2,点 在棱 上,过点 作该正方体的截面,当截面平行于平面 且面积为 时,线段 的长为( )A、 B、1 C、 D、10. 已知定义域为 的函数 满足:①图象关于原点对称;② ;③当 时, .若 ,则 ( )A、-1 B、1 C、-2 D、211. 将函数 的图象向左平移 个单位长度后得到的部分图象如图所示,有下列四个结论:① ;② 在 上有两个零点;③ 的图象关于直线 对称;④ 在区间 上单调递减,其中所有正确结论的个数为( )
A、极差为36 B、众数为34 C、中位数为27 D、平均数为324. “ ”是“函数 在 上单调递增”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 若 ,则 ( )A、-7 B、7 C、 D、6. 已知 , , ,则( )A、 B、 C、 D、7. 已知抛物线 的焦点为F,准线为l,过抛物线上一点P作 ,垂足为Q,若 ,则 ( )A、 B、 C、 D、8. 2020年是全面建成小康社会的目标实现之年,也是全面打赢脱贫攻坚战的收官之年.为更好地将“精准扶贫”落到实处,某地安排7名干部(3男4女)到三个贫困村调研走访,每个村安排男、女干部各1名,剩下1名干部负责统筹协调,则不同的安排方案有( )A、72种 B、108种 C、144种 D、210种9. 已知正方体 的棱长为2,点 在棱 上,过点 作该正方体的截面,当截面平行于平面 且面积为 时,线段 的长为( )A、 B、1 C、 D、10. 已知定义域为 的函数 满足:①图象关于原点对称;② ;③当 时, .若 ,则 ( )A、-1 B、1 C、-2 D、211. 将函数 的图象向左平移 个单位长度后得到的部分图象如图所示,有下列四个结论:① ;② 在 上有两个零点;③ 的图象关于直线 对称;④ 在区间 上单调递减,其中所有正确结论的个数为( )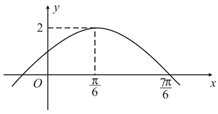 A、1 B、2 C、3 D、412. 设双曲线 的左、右焦点分别为 ,过点 的直线l与C的两支分别交于点A,B,若点M满足 , ,则双曲线C的渐近线方程为( )A、 B、 C、 D、
A、1 B、2 C、3 D、412. 设双曲线 的左、右焦点分别为 ,过点 的直线l与C的两支分别交于点A,B,若点M满足 , ,则双曲线C的渐近线方程为( )A、 B、 C、 D、二、填空题
-
13. 若实数x,y满足 ,则 的最大值为.14. 若平面向量 满足 , ,且 ,则 与 夹角的大小为.15. 在 中,内角A,B,C所对的边分别为a,b,c,若 , ,且点M满足 ,则 的长为.16. 在正三棱锥 中, ,点 是 的中点,若 ,则该三棱锥外接球的表面积为.
三、解答题
-
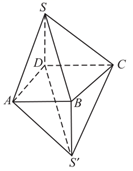
17. 已知首项为4的数列 的前n项和为 ,且 .(1)、求证:数列 为等差数列,并求数列 的通项公式;(2)、若 ,求数列 的前n项和 .18. 已知多面体 如图所示,四边形 为梯形, , 平面 , , , .
 (1)、求证: 平面 ;(2)、求平面 与平面 所成锐二面角的余弦值.19. 某高校为了加快打造一流名校步伐,生源质量不断改善.据统计,该校2014年到2020年所招的学生高考成绩不低于600分的人数y与对应年份代号x的数据如下:
(1)、求证: 平面 ;(2)、求平面 与平面 所成锐二面角的余弦值.19. 某高校为了加快打造一流名校步伐,生源质量不断改善.据统计,该校2014年到2020年所招的学生高考成绩不低于600分的人数y与对应年份代号x的数据如下:年份
2014
2015
2601
2017
2018
2019
2020
年份代号x
1
2
3
4
5
6
7
不低于600分的人数y(单位:人)
29
33
36
44
48
52
59
(1)、若y关于x具有较强的线性相关关系,求y关于x的线性回归方程 ,并预测2021年该校所招的学生高考成绩不低于600分的人数;(2)、今有 、 、 、 四位同学报考该校,已知 、 、 被录取的概率均为 , 被录取的概率为 ,且每位同学是否被录取相互不受影响,用 表示此 人中被录取的人数,求 的分布列与数学期望.参考公式: , .参考数据: , .
20. 已知椭圆 : 的离心率为 ,且过点 .(1)、求椭圆 的方程;(2)、若直线 ( 且 )交椭圆 于 , 两点,记直线 , 的斜率分别为 , ,探究: 是否为定值,若是,求出该值;若不是,请说明理由.