浙江省名校协作体2020-2021学年高二下学期数学开学考试试卷

试卷更新日期：2021-06-17 类型：开学考试

进入出卷网下载

一、单选题

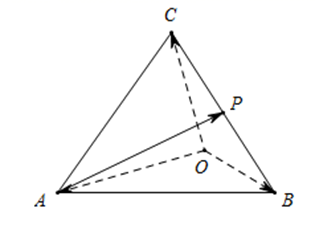
1. 直线 $x + \sqrt{3} y - 1 = 0$ 的倾斜角为（）

A、30° B、60° C、120° D、150°

查看试题解析
2. 直线 $2 x + 3 y = 0$ 是双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{4} = 1 (a > 0)$ 的一条渐近线，则实数a的值为（）

A、 $\frac{1}{3}$ B、3 C、 $\frac{4}{3}$ D、 $\frac{3}{4}$

查看试题解析
3. 已知 $m ， n$ 是两条不同直线， $α ， β ， γ$ 是三个不同平面，下列命题中正确的是（）

A、若 $m / / n ， n \subset α$ ，则 $m / / α$ B、若m $/ / α ， m / / β$ ，则 $α / / β$ C、若 $m ⊥ α ， n ⊥ α$ ，则 $m / / n$ D、若 $α ⊥ γ ， β ⊥ γ$ ，则 $α / / β$

查看试题解析
4. “ $m = - 1$ ”是“直线 $m x + (m - 1) y + 1 = 0$ 和直线 $2 x + m y + 3 = 0$ 垂直”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
5. 在四面体 $O - A B C$ 中，点 $P$ 为棱 $B C$ 的中点. 设 $\overset{⇀}{O A} = \vec{a}$ ， $\overset{⇀}{O B} = \vec{b}$ ， $\overset{⇀}{O C} = \vec{c}$ ，那么向量 $\overset{⇀}{A P}$ 用基底 ${\vec{a} ， \vec{b} ， \vec{c}}$ 可表示为（）

A、 $- \frac{1}{2} \vec{a} + \frac{1}{2} \vec{b} + \frac{1}{2} \vec{c}$ B、 $- \vec{a} + \frac{1}{2} \vec{b} + \frac{1}{2} \vec{c}$ C、 $\vec{a} + \frac{1}{2} \vec{b} + \frac{1}{2} \vec{c}$ D、 $\frac{1}{2} \vec{a} + \frac{1}{2} \vec{b} + \frac{1}{2} \vec{c}$

查看试题解析
6. 已知平面 $α$ 和两条异面直线 $a ， b$ 满足 $a \subset α ， b ⊥ α$ ，平面 $α$ 内的动点 $M$ 到两条直线 $a ， b$ 的距离相等，则点 $M$ 的轨迹是（）

A、两条直线 B、椭圆 C、双曲线 D、抛物线

查看试题解析
7. 圆 $x^{2} + y^{2} - m x + y + m = 0$ 在 $x$ 轴上截得的弦长是它在 $y$ 轴上截得的弦长的2倍，则实数 $m$ 的值是（）

A、 $- 6 - 2 \sqrt{10}$ B、 $- 6 + 2 \sqrt{10}$ C、 $- 3 - \sqrt{10}$ D、 $- 3 + \sqrt{10}$

查看试题解析
8. 正三棱锥 $A - B C D$ 中，二面角 $A - B C - D$ 的大小为 $α$ ，二面角 $B - A C - D$ 的大小为 $β$ ，则 ${cos}^{2} α + cos β$ 的取值范围是（）

A、 $(- \frac{1}{2} ， \frac{2}{3})$ B、 $(0 ， \frac{1}{2})$ C、 $(0 ， \frac{2}{3})$ D、 $(\frac{1}{2} ， \frac{2}{3})$

查看试题解析
9. 曲线 $C_{1} ： y^{2} = 6 | x |$ 与 $C_{2} ： \frac{y | y |}{4} - \frac{x | x |}{3} = 1$ 交点的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
10. 在正四面体 $A B C D$ 中， $P ， Q$ 分别是棱 $A B ， C D$ 的中点， $E ， F$ 分别是直线 $A B ， C D$ 上的动点，且满足 $| P E | + | Q F | = a$ ， $M$ 是 $E F$ 的中点，则点 $M$ 的轨迹围成的区域的面积是（）

A、 $\frac{a^{2}}{4}$ B、 $\frac{a^{2}}{2}$ C、 $\frac{π a^{2}}{4}$ D、 $\frac{π a^{2}}{2}$

查看试题解析

二、填空题

11. 已知抛物线 $C$ 的焦点 $F (1 ， 0)$ ，则拋物线C的标准方程为，焦点到准线的距离为.

查看试题解析
12. 已知某几何体的三视图如图，则该几何体的体积为 ${cm}^{3} ，$ 表面积为 ${cm}^{2}$ .

查看试题解析
13. 若直线 $l_{1} ： y = k x + 1$ 与直线 $l_{2}$ 关于点(2，3)对称，则直线 $l_{2}$ 恒过定点的坐标为，直线 $l_{1}$ 与 $l_{2}$ 的距离的最大值是.

查看试题解析
14. 已知 $P$ 是圆 $C ： {(x - 3)}^{2} + {(y - 4)}^{2} = 1$ 上一动点，过圆心 $C$ 作两条互相垂直的直线 $l_{1} ， l_{2}$ ，它们分别交 $x$ 轴于 $A$ 点，交 $y$ 轴于 $B$ 点，记 $A B$ 中点为 $Q$ ，则 $P Q$ 的最小值是，圆 $C$ 上到 $Q$ 的距离等于3的点有个.

查看试题解析

三、填空题

15. 已知平面 $α / / β$ ，直线 $l$ 与 $α$ 所成角的正切值为 $\frac{\sqrt{2}}{2}$ ，直线 $m \subset α ， l ⊥ m$ ，直线 $n \subset β$ ，且 $l$ 和 $n$ 所成角为 $\frac{π}{4}$ ，那么 $m$ 与 $n$ 所成的角为.

查看试题解析
16. 已知椭圆 $C ： \frac{x^{2}}{3} + y^{2} = 1 ，$ 过 $C$ 上一点 $P ($ 第一象限 $)$ 的直线 $l$ 与 $x$ 轴正半轴， $y$ 轴正半轴分别交于点 $A ， B .$ 若 $| P A | = 1$ ，则 $| P B |$ 的值为.

查看试题解析
17. 如图，双曲线 $C_{1} ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的右焦点 $F$ 是拋物线 $C_{2} ： y^{2} = 2 p x$ 的焦点， $O$ 为坐标原点， $A$ 为双曲线 $C_{1}$ 与拋物线 $C_{2}$ 在第一象限内的交点，若 $\vec{O F} \cdot \vec{A F} = \frac{| \vec{F A} |^{2}}{4} ，$ 则双曲线 $C_{1}$ 的离心率是.

查看试题解析

四、解答题

18. 已知圆 $C$ 经过 $M (1 ， 0) ， N (2 ， 1)$ 两点，且圆心 $C$ 在直线 $x + 2 y - 2 = 0$ 上.

(1)、求圆 $C$ 的方程；

(2)、过点 $P (0 ， 1)$ 的直线 $l$ 与圆 $C$ 交于不同的 $A ， B$ 两点，且 $C A ⊥ C B$ ，求直线 $l$ 的方程.

查看试题解析
19. 如图，已知三棱锥 $P - A B C$ 中， $A B = B C = 2 ， P A = P C = P B = \sqrt{3}$ ，且 $A B ⊥ B C$ .

(1)、求证： $A C ⊥ P B$ ；

(2)、求二面角 $P - B C - A$ 的大小.

查看试题解析
20. 如图，已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{\sqrt{3}}{2}$ ，且过点 $(1 ， \frac{\sqrt{3}}{2})$ .

(1)、求椭圆 $C$ 的标准方程；

(2)、过左焦点 $F$ 且斜率为正的直线 $l$ 与椭圆 $C$ 交于 $A$ 、 $B$ 两点，过点 $A$ 、 $B$ 分别作与直线 $l$ 垂直的直线，交 $x$ 轴于 $C$ 、 $D$ 两点，求 $| F C | \cdot | F D |$ 的最小值.

查看试题解析
21. 在三棱台 $A B C - D E F$ 中， $A B = B C = 2 D E ， ∠ D A B = ∠ E B A = 60^{\circ}$ ，平面 $A B E D ⊥$ 平面 $A B C ， B C ⊥ B E .$

(1)、求证：平面 $A B E D ⊥$ 平面 $B C F E$ ；

(2)、求直线 $D F$ 与平面 $A B F$ 所成角的正弦值.

查看试题解析
22. 如图，已知过拋物线 $C ： y^{2} = 4 x$ 的焦点 $F$ 的直线交抛物线 $C$ 于点 $A ， B ($ 点 $A$ 在第一象限)，线段 $A B$ 的中点为 $M ，$ 拋物线 $C$ 在点 $A$ 处的切线与以 $A M$ 为直径的圆交于另一点 $P$ .

(1)、若 $\vec{A F} = 4 \vec{F B}$ ，求直线 $A B$ 的方程；

(2)、试问 $\frac{| A P |^{2}}{| A B | \cdot | A F |}$ 是否为定值？若是，请求出该定值；若不是，请求出它的最大值.

查看试题解析