重庆市南岸区2021年数学中考模拟试卷

试卷更新日期：2021-06-17 类型：中考模拟

进入出卷网下载

一、单选题

1. 3的绝对值是 ( )

A、－3 B、3 C、 $- \frac{1}{3}$ D、 $\frac{1}{3}$

查看试题解析
2. 若 $x = 3$ ，则代数式 $2 x + 3$ 的值是（）

A、6 B、8 C、9 D、26

查看试题解析
3. 如图，在 $Δ A B C$ 中， $C D$ 是高， $C M$ 是中线，点 $C$ 到 $A B$ 边的距离是（）

A、 $C D$ 的长 B、 $C A$ 的长 C、 $C M$ 的长 D、 $C B$ 的长

查看试题解析
4. 如图，已知四边形ABCD内接于⊙O，∠ABC=70°，则∠ADC的度数是（　　）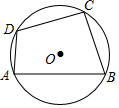

A、70° B、110° C、130° D、140°

查看试题解析
5. 实数 $a$ 在数轴上对应点的位置如图所示．若实数 $b$ 满足 $a < b < 2$ ，则 $b$ 的值可以是（）

A、-2 B、-1 C、2 D、3

查看试题解析
6. 如图，以点O为位似中心，将 $△ A B C$ 缩小后得到 $△ A' B' C'$ ，已知 $O B = 3 O B'$ ，则 $△ A' B' C'$ 与 $△ A B C$ 的面积的比为 $($ $)$

A、1：3 B、1：4 C、1：5 D、1：9

查看试题解析
7. 计算 $\sqrt{8} - \sqrt{2}$ 的结果是（）

A、 $\sqrt{2}$ B、 $\sqrt{6}$ C、2 D、4

查看试题解析
8. 在解方程 $\frac{x - 1}{3} + x = \frac{3 x + 1}{2}$ 时，方程两边同时乘以6，去分母后，正确的是（）

A、2x﹣1+6x=3（3x+1） B、2（x﹣1）+6x=3（3x+1） C、2（x﹣1）+x=3（3x+1） D、（x﹣1）+x=3（x+1）

查看试题解析
9. 如图，某学校后坡有一个凉亭在点 $C$ 处，通往凉亭要走两段坡度不一样的阶梯 $A B$ 和 $B C ， A B$ 部分的坡角为 $32^{°}$ ， $B C$ 部分的坡度（或坡比) $i = 1 ： 2.4$ ．已知 $A B$ 和 $B C$ 两段阶梯的台阶数量相同，每个台阶的高度也相同，若第一段坡长 $A B = 30 m$ ，则第二段坡长 $B C$ 约为（）（参考数据： $\sin 32^{°} \approx 0.53 ， \cos 32^{°} \approx 0.85 ， \tan 32^{°} \approx 0.62$ ）

A、 $38.2 m$ B、 $41.3 m$ C、 $48.4 m$ D、 $66.3 m$

查看试题解析
10. 如图，在直角坐标系中，矩形 $O A B C$ 的边 $O A ， O C$ 分别在 $x$ 轴和 $y$ 轴上，对角线 $O B$ 的中点 $D$ 在反比例函数 $y = \frac{6}{x} (x > 0)$ 的图象上， $D E / / x$ 轴，交 $A B$ 于点 $E$ ．过点 $E$ 的反比例函数 $y = \frac{n}{x} (x > 0)$ 的图象交 $O B$ 于点 $F$ ，连接 $C F$ ．若点 $D (3 ， m)$ ，则 $Δ C O F$ 的面积为（）

A、 $3 \sqrt{2}$ B、 $4 \sqrt{2}$ C、 $6 \sqrt{2}$ D、 $8 \sqrt{2}$

查看试题解析
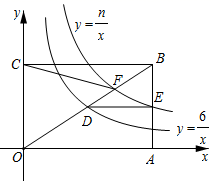11. 若数 $a$ 使关于 $x$ 的一元一次不等式组 ${\begin{array}{l} \frac{x + 1}{5} \geq \frac{x}{2} - 1 \\ x + a < 6 x + 3 \end{array}$ ，至少有4个整数解，且使关于 $y$ 的分式方程 $\frac{y + a}{y - 3} + \frac{2 y}{3 - y} = 1$ 有非负整数解，则符合条件的所有整数 $a$ 的值之和为（）

A、9 B、12 C、15 D、19

查看试题解析
12. 如图，在纸片 $Δ A B C$ 中， $A B = A C = 12 ， ∠ B = 30^{°}$ ，折叠纸片，使点 $B$ 落在 $A C$ 的中点 $D$ 处，折痕为 $E F$ ，则 $Δ D E F$ 的面积为（）

A、 $\frac{49 \sqrt{3}}{5}$ B、 $10 \sqrt{3}$ C、 $11 \sqrt{3}$ D、 $\frac{56 \sqrt{3}}{5}$

查看试题解析

二、填空题

13. 计算： ${(π - 3)}^{0} + {(- 1)}^{3} =$ ．

查看试题解析
14. 三张背面完全相同的卡片，正面分别写着数字 $1 ， 2 ， 3$ ．背面朝上，随机抽取一张记下数字后，放回搅匀，再随机抽取一张，则两次取出的数字之和是偶数的概率为．

查看试题解析
15. 如图，点 $C ， D$ 分别是以 $A B$ 为直径的半圆上的三等分点，若阴影部分的面积是 $\frac{3}{2} π$ ，则弧 $C D$ 的长为．

查看试题解析
16. 小明家、文具店、学校在一条直线上，小明家到学校的路程为 $1000 m$ ．一天，小明在上学途中到文具店买了学习用品，然后以原速的 $1.5$ 倍继续匀速步行到学校，图中的折线反映了这天小明从家步行到学校所走的路程 $s (m)$ 与时间 $t (\min)$ 之间的函数关系，这天小明上学途中共用的时间是 $\min$

查看试题解析
17. 如图，四边形 $A B C D$ 是菱形，点 $E ， F$ 分别在边 $B C ， C D$ 上，其中 $C E = \frac{1}{3} B C ， C F = \frac{1}{3} C D ， P$ 是对角线 $B D$ 上的动点，若 $P E + P F$ 的最小值为 $4 \sqrt{2} ， A C = 6$ ，则该菱形的面积为

查看试题解析
18. 随着我国疫情的有效控制，各地打造了众多春游景点供市民休闲娱乐．某区特别打造了多彩植物园、亲子游乐园、劳动体验园吸引游客.3月份多彩植物园、亲子游乐园、劳动体验园接待游客数量之比为 $3 ： 3 ： 4$ ．为增加游客数量，该地区通过发抖音、转发朋友圈等多种方式加大宣传力度，预计4月份三个园区接待的游客总人数在3月份的基础上会增加．但因为多彩植物园中部分花期已过，多彩植物园的游客人数在3月份的基础上将减少 $\frac{1}{3}$ ．这样4月份，多彩植物园接待的游客总人数占三个园区接待游客总人数的 $\frac{1}{7}$ ，而亲子游乐园、劳动体验园4月份接待游客人数之比将达到 $3 ： 2$ ，则亲子游乐园新增的人数与4月份这三个园区的总人数之比是

查看试题解析

三、解答题

19. 计算：

(1)、 $x (x + 2 y) + {(x - y)}^{2}$

(2)、 $a - 1 + \frac{2 a - 6}{a^{2} - 9} \div \frac{2 a + 2}{a + 3}$

查看试题解析
20. 如图，已知 $Δ A B C .$

(1)、作 $∠ A C B$ 的平分线，交 $A B$ 于点 $D$ ；以 $D$ 为顶点，在边 $A B$ 右侧作 $∠ A D E = ∠ A B C$ ，交 $A C$ 于点 $E$ ；（要求：尺规作图，不写作法，保留作图痕迹）

(2)、在（1）所作的图中，求证： $D E = C E .$

查看试题解析

21. 某中学九年级共750名学生参加了中招体考，现从甲、乙两个班级各随机抽取10名学生的中招体考成绩(50分制)进行整理、描述和分析(成绩得分用

m

表示，共分成三组：

A .0 \leq m < 45 ， B .45 < m < 49 ， C . m = 50

)．下面给出了部分信息：其中乙班

B

组的数据为：

49 ， 48 ， 48 ， 48 ， 48.

抽取的甲、乙两班各10名学生的中招体考成绩统计表

班级	平均数	中位数	众数	优秀率
甲班	47	$x$	$z$	70%
乙班	47	$y$	48/	80%

根据以上信息，解答下列问题：

(1)、直接写出

x ， y ， z

的值；

(2)、你认为该校九年级中招体考成绩，甲、乙两个班级，哪个班成绩较好，请说明理由（写出一条理由即可)；

(3)、估计该校九年级学生中招体考成绩达到满分的人数．

查看试题解析

22. 在初中阶段的函数学习中，我们经历了列表、描点、连线画函数图象，并结合图象研究函数性质的过程．以下是我们研究函数

y = \frac{12}{| x | + 1}

的性质及其应用的部分过程，按要求完成下列各小题．

(1)、请把下表补充完整，并在图中补全该函数图象；

$x$	…	-5	-4	-3	-2	-1	0	1	2	3	4	5	…
$y = \frac{12}{\| x \| + 1}$	…		$\frac{12}{5}$	3	4	6			4		$\frac{12}{5}$	2	…

(2)、请根据这个函数的图象，写出这个函数的一条性质；

(3)、已知函数

y = x + 7

的图象如图所示，结合图象，请直接写出

x + 7 > \frac{12}{| x | + 1}

的解集．(近似值保留一位小数，误差不超过

0.2

)

查看试题解析

23. 毕业季即将到来，某礼品店购进了一批适合大学生的毕业纪念品，该礼品店用4000元购进 $A$ 种礼品若干件，用8400元购进 $B$ 种礼品若干件，所购 $B$ 种礼品的数量比 $A$ 种礼品的数量多10件，且 $B$ 种礼品每件的进价是 $A$ 种礼品每件进价的1.4倍．

(1)、 $A ， B$ 两种礼品每件的进价分别为多少元?

(2)、礼品店第一次所购礼品全部售完后，再次购进 $A ， B$ 两种礼品(进价不变)，其中 $A$ 种礼品购进的数量在第一次的基础上增加了 $2 a %$ ，售价在进价的基础上提高了 $0.9 a %$ ； $B$ 种礼品购进的数量在第一次的基础上增加了 $2 a %$ ，售价在进价的基础上提高了 $a %$ ．全部售出后，第二次所购礼品的利润为12000元(不考虑其他因素)，求第二次购进 $A ， B$ 两种礼品各多少件?

查看试题解析
24. “字母表示数”的系统化阐述是由16世纪法国数学家韦达提出的，被后人称为从“算术”到“代数”的一次飞跃，从而大大推动了数学的发展．经过初中三年数学的学习，我们知道了用字母表示数可以分析从特殊到一般的数学规律，字母与数一样，也可以参与运算．请同学们观察下列等式：
第1个等式： $1 \times 3 \times 5 \times 7 + 16 = 11^{2}$ ；

第2个等式： $2 \times 4 \times 6 \times 8 + 16 = 20^{2}$ ；

第3个等式： $3 \times 5 \times 7 \times 9 + 16 = 31^{2}$ ；

第4个等式： $4 \times 6 \times 8 \times 10 + 16 = 44^{2}$ ；

第5个等式： $5 \times 7 \times 9 \times 11 + 16 = 59^{2}$ ；

……

按照以上规律，解答下列问题：

(1)、写出第6个等式和第7个等式；

(2)、用字母 $n$ 表示第 $n$ 个等式（其中 $n$ 为正整数)；

(3)、若 $x (x + 2) (x + 4) (x + 6) + 16 = y^{2}$ ，且 $100 \leq y \leq 200$ ，求正整数 $x$ 的值．

查看试题解析
25. 如图所示，在平面直角坐标系由．抛物线 $y = - x^{2} + b x + c$ 与 $x$ 轴的两个交点分别为 $A (- 2 ， 0) ， B (5 ， 0)$ ，点 $C$ 在抛物线上，且直线 $A C$ 与 $x$ 轴形成的夹角为 $45^{°}$ ．

(1)、求该抛物线的函数表达式；

(2)、若点 $P$ 为直线 $A C$ 上方抛物线上的动点，求点 $P$ 到直线 $A C$ 距离的最大值；

(3)、将满足（2）中到直线 $A C$ 距离最大时的点 $P$ ，向下平移4个单位长度得到点 $Q$ ，将原抛物线向右平移2个单位长度，得到抛物线 $y = a_{1} x^{2} + b_{1} x + c_{1} (a_{1} \neq 0) ， M$ 为平移后抛物线上的动点， $N$ 为平移后抛物线对称轴上的动点，是否存在点 $M$ ，使得以点 $C ， Q ， M ， N$ 为顶点的四边形是平行四边形，若存在，请直接写出点 $M$ 的坐标；若不存在，请说明理由．

查看试题解析
26. 如图所示，在 $▱ A B C D$ 中，连接对角线 $A C$ ．把 $A B$ 绕着点 $A$ 逆时针旋转 $60^{°}$ ，得到线段 $A E$ ，点 $E$ 在边 $B C$ 上．点 $F$ 在线段 $A E$ 上，且 $A F = C E$ ．连接 $B F ， D F . G$ 是 $B F$ 的中点，连接 $A G ， C G$

(1)、求证： $∠ B A G = ∠ E A C$ ；

(2)、猜想 $A G$ 与 $C G$ 存在的数量关系，并证明你猜想的结论；

(3)、当 $∠ B A G = 15^{°}$ 时，请直接写出 $D F$ 与 $A B$ 存在的数量关系．

查看试题解析