浙江省绍兴市新昌县2021年初中学业模拟考试数学试卷
试卷更新日期:2021-06-17 类型:中考模拟
一、单选题
-
1. -5的绝对值等于( )A、-5 B、5 C、 D、2. 截止2021年2月28日,全球新冠肺炎累计确诊病例超113000000,数字113000000月科学记数法可简洁表示为( )A、 B、 C、 D、3.
如图所示的几何体的俯视图为 ( )
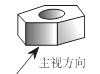 A、
A、 B、
B、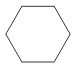 C、
C、 D、
D、 4. 计算 的正确结果是( )A、 B、 C、 D、5. 在一个有15万人的小镇,随机调查了3000人,其中有300人看中央电视台的早间新闻.据此,估计该镇看中央电视台早间新闻的约有( )A、2.5万人 B、2万人 C、1.5万人 D、1万人6. 如图, 是等腰三角形 的顶角平分线, ,则 等于( )
4. 计算 的正确结果是( )A、 B、 C、 D、5. 在一个有15万人的小镇,随机调查了3000人,其中有300人看中央电视台的早间新闻.据此,估计该镇看中央电视台早间新闻的约有( )A、2.5万人 B、2万人 C、1.5万人 D、1万人6. 如图, 是等腰三角形 的顶角平分线, ,则 等于( )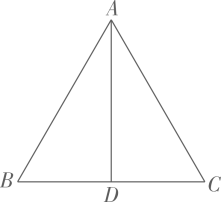 A、10 B、5 C、4 D、37. 三角板是我们学习数学的工具,一副三角板拼成如图方式,则图中 的值为( )
A、10 B、5 C、4 D、37. 三角板是我们学习数学的工具,一副三角板拼成如图方式,则图中 的值为( )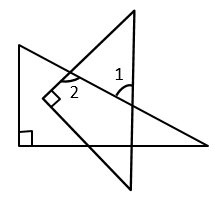 A、30° B、45° C、60° D、不能确定8. 《孙子算经》是中国古代重要的数学著作,书中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有 匹,则可列方程为( )A、 B、 C、 D、9. 如图,一次函数 与y轴相交于点 ,与 轴相交于点 ,在直线 上取一点 (点 不与 , 重合),过点 作 轴,垂足为点 ,连结 ,若 的面积恰好为 ,则满足条件的 点有( )
A、30° B、45° C、60° D、不能确定8. 《孙子算经》是中国古代重要的数学著作,书中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有 匹,则可列方程为( )A、 B、 C、 D、9. 如图,一次函数 与y轴相交于点 ,与 轴相交于点 ,在直线 上取一点 (点 不与 , 重合),过点 作 轴,垂足为点 ,连结 ,若 的面积恰好为 ,则满足条件的 点有( ) A、1个 B、2个 C、3个 D、4个10. 如图, 中, , , ,平行四边形内放着两个菱形,菱形 和菱形 ,它们的重叠部分是平行四边形 .已知三个阴影平行四边形的周长相等,那么平行四边形 的面积为( )
A、1个 B、2个 C、3个 D、4个10. 如图, 中, , , ,平行四边形内放着两个菱形,菱形 和菱形 ,它们的重叠部分是平行四边形 .已知三个阴影平行四边形的周长相等,那么平行四边形 的面积为( )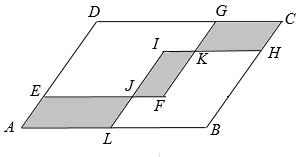 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 因式分解: .12. 如图,在 中,若 是 的中点, 是 的中点, ,则 度.
 13. 如图,已知点 是圆 上一点,以点 为圆心, 为半径作弧,交圆 于点 ,则 的度数为度.
13. 如图,已知点 是圆 上一点,以点 为圆心, 为半径作弧,交圆 于点 ,则 的度数为度.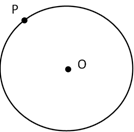 14. 将二次函数 的图象向左平移3个单位,再向下平移3个单位,则平移后的二次函数的最小值为.15. 如图是4个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作 ( 为1~4的整数),函数 ( )的图象为曲线 .若曲线 使得 ,这些点分布在它的两侧,每侧各2个点,则 的取值范围是.
14. 将二次函数 的图象向左平移3个单位,再向下平移3个单位,则平移后的二次函数的最小值为.15. 如图是4个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作 ( 为1~4的整数),函数 ( )的图象为曲线 .若曲线 使得 ,这些点分布在它的两侧,每侧各2个点,则 的取值范围是. 16. 如图,在矩形 中, .将矩形 绕点 按顺时针方向旋转,旋转角为 ( ),得到矩形 ,边 与 相交于点 ,边 与 的延长线相交于点 .在矩形 旋转过程中,当 落在线段 上时, , 当 是线段 的三等分点时, .
16. 如图,在矩形 中, .将矩形 绕点 按顺时针方向旋转,旋转角为 ( ),得到矩形 ,边 与 相交于点 ,边 与 的延长线相交于点 .在矩形 旋转过程中,当 落在线段 上时, , 当 是线段 的三等分点时, .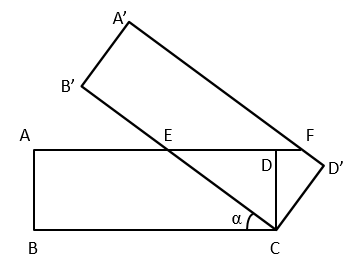
三、解答题
-
17.(1)、计算:(2)、解方程:18. 一辆客车从甲地开往乙地,一辆轿车从乙地开往甲地,两车同时出发,如图表示两车行驶时间 (小时)与到甲地的距离 (千米)的函数图象,已知其中一个函数的表达式为 .
 (1)、求另一个函数表达式.(2)、求两车相遇的时间.19. 某校九(1)班针对“垃圾分类”知晓情况对全班学生进行专题调查活动,将“垃圾分类”的知晓情况分为 , , , 四类,其中, 类表示“非常了解”, 类表示“比较了解”, 类表示“基本了解”, 类表示“不太了解”,每名学生可根据自己的情况任选其中一类,班长根据调查结果进行了统计,并绘制成了不完整的条形统计图和扇形统计图.
(1)、求另一个函数表达式.(2)、求两车相遇的时间.19. 某校九(1)班针对“垃圾分类”知晓情况对全班学生进行专题调查活动,将“垃圾分类”的知晓情况分为 , , , 四类,其中, 类表示“非常了解”, 类表示“比较了解”, 类表示“基本了解”, 类表示“不太了解”,每名学生可根据自己的情况任选其中一类,班长根据调查结果进行了统计,并绘制成了不完整的条形统计图和扇形统计图.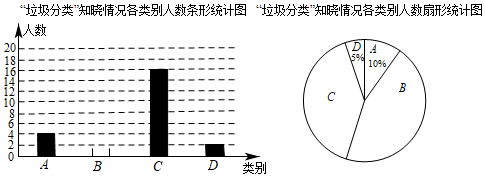
根据以上信息解决下列问题:
(1)、补全条形统计图,并求出扇形统计图中类别 所对应扇形的圆心角度数.(2)、类别 的4名学生中有3名男生和1名女生,现从这4名学生中随机选取2名学生参加学校“垃圾分类”知识竞赛,求所选取的2名学生中恰好有1名男生、1名女生的概率.20. 如图是边长为1的小正三角形组成的网格. (1)、在网格中画出一个以 为边的 ,使 的长为无理数且 , 均在格点(即每个小正三角形的顶点)上.(2)、针对你所画的平行四边形(不添加任何条件),请你编制一个计算题,并直接写出答案.21. 如图,一个书架上的方格中放着七本厚度和长度相同的书,其中左边六本书紧帖书架方格内侧竖放,右边一本书自然向左斜放,支撑点为 , ,右侧书角 正好靠在方格内侧上.若书架方格内侧长 , ,书的长度 .
(1)、在网格中画出一个以 为边的 ,使 的长为无理数且 , 均在格点(即每个小正三角形的顶点)上.(2)、针对你所画的平行四边形(不添加任何条件),请你编制一个计算题,并直接写出答案.21. 如图,一个书架上的方格中放着七本厚度和长度相同的书,其中左边六本书紧帖书架方格内侧竖放,右边一本书自然向左斜放,支撑点为 , ,右侧书角 正好靠在方格内侧上.若书架方格内侧长 , ,书的长度 . (1)、求 的长度.(2)、求每本书的厚度.(结果精确到 )(参考数据: , , )22. 如图,在 中, .点 为边 上一点, 于点 ,点 为 上一点.连结 并延长与 相交于点 ,连结 .已知 .
(1)、求 的长度.(2)、求每本书的厚度.(结果精确到 )(参考数据: , , )22. 如图,在 中, .点 为边 上一点, 于点 ,点 为 上一点.连结 并延长与 相交于点 ,连结 .已知 . (1)、若 平分 ,求证: ≌ .(2)、若 ,求 的长.(3)、若 ,求 的读数.23. 某喷泉中间的喷水管 ,喷水点 向各个方向喷射出去的水柱为形状相同的抛物线,以水平方向为 轴,喷水管所在直线为 轴,喷水管与地面的接触点 为原点建立直角坐标系,如图所示,已知喷出的水柱距原点 处达到最高,高度为 .
(1)、若 平分 ,求证: ≌ .(2)、若 ,求 的长.(3)、若 ,求 的读数.23. 某喷泉中间的喷水管 ,喷水点 向各个方向喷射出去的水柱为形状相同的抛物线,以水平方向为 轴,喷水管所在直线为 轴,喷水管与地面的接触点 为原点建立直角坐标系,如图所示,已知喷出的水柱距原点 处达到最高,高度为 . (1)、求水柱所在抛物线(第一象限)的函数表达式.(2)、身高为 的小明站在距离喷水管 的地方,他会被水喷到吗?(3)、现重新改建喷泉,升高喷水管,使落水点与喷水管距离 ,已知喷水管升高后,喷水管喷出的水柱抛物线形状不变,且水柱仍在距离原点 处达到最高,则喷水管 要升高多少?24. 如图,在矩形 中, , ,点 是 上一点,且 , 是边 上的动点,以 为边作矩形 ,使 ,矩形 是矩形 关于对角线 的轴对称图形.
(1)、求水柱所在抛物线(第一象限)的函数表达式.(2)、身高为 的小明站在距离喷水管 的地方,他会被水喷到吗?(3)、现重新改建喷泉,升高喷水管,使落水点与喷水管距离 ,已知喷水管升高后,喷水管喷出的水柱抛物线形状不变,且水柱仍在距离原点 处达到最高,则喷水管 要升高多少?24. 如图,在矩形 中, , ,点 是 上一点,且 , 是边 上的动点,以 为边作矩形 ,使 ,矩形 是矩形 关于对角线 的轴对称图形. (1)、当 时,求矩形 的面积.(2)、当点 落在 上时,求 .(3)、在 从 到 的运动过程中,
(1)、当 时,求矩形 的面积.(2)、当点 落在 上时,求 .(3)、在 从 到 的运动过程中,①当 落在边 上时,求 的长.
②当矩形 与矩形 的边只有两个交点时,直接写出 的取值范围.