四川省遂宁市2021年中考数学试卷
试卷更新日期:2021-06-17 类型:中考真卷
一、单选题
-
1. -2021的绝对值是( )A、-2021 B、2021 C、 D、2. 下列计算中,正确的是( )A、 B、 C、 D、3. 如图所示的几何体是由6个完全相同的小正方体搭成,其主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 国家统计局2021年5月11日公布了第七次全国人口普查结果,全国总人口约14.1亿人,将14.1亿用科学记数法表示为( )A、14.1×108 B、1.41×108 C、1.41×109 D、0.141×10105. 如图,在△ABC中,点D、E分别是AB、AC的中点,若△ADE的面积是3cm2 , 则四边形BDEC的面积为( )
4. 国家统计局2021年5月11日公布了第七次全国人口普查结果,全国总人口约14.1亿人,将14.1亿用科学记数法表示为( )A、14.1×108 B、1.41×108 C、1.41×109 D、0.141×10105. 如图,在△ABC中,点D、E分别是AB、AC的中点,若△ADE的面积是3cm2 , 则四边形BDEC的面积为( ) A、12cm2 B、9cm2 C、6cm2 D、3cm26. 下列说法正确的是( )A、角平分线上的点到角两边的距离相等 B、平行四边形既是轴对称图形,又是中心对称图形 C、在代数式 , , , , , 中, , , 是分式 D、若一组数据2、3、x、1、5的平均数是3,则这组数据的中位数是47. 不等式组 的解集在数轴上表示正确的是( )A、
A、12cm2 B、9cm2 C、6cm2 D、3cm26. 下列说法正确的是( )A、角平分线上的点到角两边的距离相等 B、平行四边形既是轴对称图形,又是中心对称图形 C、在代数式 , , , , , 中, , , 是分式 D、若一组数据2、3、x、1、5的平均数是3,则这组数据的中位数是47. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、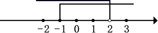 D、
D、 8. 如图,在矩形ABCD中,AB=5,AD=3,点E为BC上一点,把△CDE沿DE翻折,点C 恰好落在AB边上的F处,则CE的长是( )
8. 如图,在矩形ABCD中,AB=5,AD=3,点E为BC上一点,把△CDE沿DE翻折,点C 恰好落在AB边上的F处,则CE的长是( ) A、1 B、 C、 D、9. 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为点F,若⊙O的半径为 ,∠CDF=15°, 则阴影部分的面积为( )
A、1 B、 C、 D、9. 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为点F,若⊙O的半径为 ,∠CDF=15°, 则阴影部分的面积为( ) A、 B、 C、 D、10. 已知二次函数 的图象如图所示,有下列5个结论:① ;② ;③ ;④ ( );⑤若方程 =1有四个根,则这四个根的和为2,其中正确的结论有( )
A、 B、 C、 D、10. 已知二次函数 的图象如图所示,有下列5个结论:① ;② ;③ ;④ ( );⑤若方程 =1有四个根,则这四个根的和为2,其中正确的结论有( )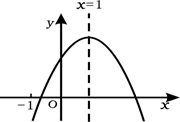 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 若 ,则 .12. 如图,在△ABC中,AB=5,AC=7,直线DE垂直平分BC,垂足为E,交AC于点D,则△ABD的周长是.
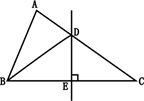 13. 已知关于x,y的二元一次方程组 满足 ,则a的取值范围是.14. 如图都是由同样大小的小球按一定规律排列的,依照此规律排列下去,第个图形共有210个小球.
13. 已知关于x,y的二元一次方程组 满足 ,则a的取值范围是.14. 如图都是由同样大小的小球按一定规律排列的,依照此规律排列下去,第个图形共有210个小球. 15. 如图,正方形ABCD中,点E是CD边上一点,连结BE,以BE为对角线作正方形BGEF,边EF与正方形ABCD的对角线BD相交于点H,连结AF,有以下五个结论:① ;② ;③ ;④ ;⑤若 ,则 ,你认为其中正确是(填写序号)
15. 如图,正方形ABCD中,点E是CD边上一点,连结BE,以BE为对角线作正方形BGEF,边EF与正方形ABCD的对角线BD相交于点H,连结AF,有以下五个结论:① ;② ;③ ;④ ;⑤若 ,则 ,你认为其中正确是(填写序号)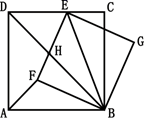
三、解答题
-
16. 计算:17. 先化简,再求值: ,其中m是已知两边分别为2和3的三角形的第三边长,且m是整数.18. 如图,在平行四边形ABCD中,对角线AC与BD相交于点O,过点O的直线EF与BA、DC的延长线分别交于点E、F.
 (1)、求证:AE=CF;(2)、请再添加一个条件,使四边形BFDE是菱形,并说明理由.19. 我市于2021年5月22-23日在遂宁观音湖举行了“龙舟赛”,吸引了全国各地选手参加.现对某校初中1000名学生就“比赛规则”的了解程度进行了抽样调查(参与调查的同学只能选择其中一项),并将调查结果绘制出以下两幅不完整的统计图表,请根据统计图表回答下列问题:
(1)、求证:AE=CF;(2)、请再添加一个条件,使四边形BFDE是菱形,并说明理由.19. 我市于2021年5月22-23日在遂宁观音湖举行了“龙舟赛”,吸引了全国各地选手参加.现对某校初中1000名学生就“比赛规则”的了解程度进行了抽样调查(参与调查的同学只能选择其中一项),并将调查结果绘制出以下两幅不完整的统计图表,请根据统计图表回答下列问题:类别
频数
频率
不了解
10
m
了解很少
16
0.32
基本了解
b
很了解
4
n
合计
a
1
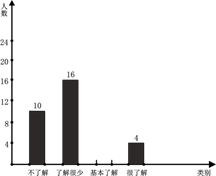 (1)、根据以上信息可知:a= , b= , m= , n=;(2)、补全条形统计图;(3)、估计该校1000名初中学生中“基本了解”的人数约有人;(4)、“很了解”的4名学生是三男一女,现从这4人中随机抽取两人去参加全市举办的“龙舟赛”知识竞赛,请用画树状图或列表的方法说明,抽到两名学生均为男生和抽到一男一女的概率是否相同.20. 已知平面直角坐标系中,点P( )和直线Ax+By+C=0(其中A,B不全为0),则点P到直线Ax+By+C=0的距离d可用公式 来计算.
(1)、根据以上信息可知:a= , b= , m= , n=;(2)、补全条形统计图;(3)、估计该校1000名初中学生中“基本了解”的人数约有人;(4)、“很了解”的4名学生是三男一女,现从这4人中随机抽取两人去参加全市举办的“龙舟赛”知识竞赛,请用画树状图或列表的方法说明,抽到两名学生均为男生和抽到一男一女的概率是否相同.20. 已知平面直角坐标系中,点P( )和直线Ax+By+C=0(其中A,B不全为0),则点P到直线Ax+By+C=0的距离d可用公式 来计算.例如:求点P(1,2)到直线y=2x+1的距离,因为直线y=2x+1可化为2x-y+1=0,其中A=2,B=-1,C=1,所以点P(1,2)到直线y=2x+1的距离为: .
根据以上材料,解答下列问题:
(1)、求点M(0,3)到直线 的距离;(2)、在(1)的条件下,⊙M的半径r = 4,判断⊙M与直线 的位置关系,若相交,设其弦长为n,求n的值;若不相交,说明理由.21. 某服装店以每件30元的价格购进一批T恤,如果以每件40元出售,那么一个月内能售出300件,根据以往销售经验,销售单价每提高1元,销售量就会减少10件,设T恤的销售单价提高x元.(1)、服装店希望一个月内销售该种T恤能获得利润3360元,并且尽可能减少库存,问T恤的销售单价应提高多少元?(2)、当销售单价定为多少元时,该服装店一个月内销售这种T恤获得的利润最大?最大利润是多少元?22. 小明周末与父母一起到遂宁湿地公园进行数学实践活动,在A处看到B、C处各有一棵被湖水隔开的银杏树,他在A处测得B在北偏西45°方向, C在北偏东30°方向,他从A处走了20米到达B处,又在B处测得C在北偏东60°方向.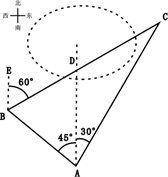 (1)、求∠C的度数;(2)、求两颗银杏树B、C之间的距离(结果保留根号).23. 如图,一次函数 =k x + b (k≠0)与反比例函数 (m≠0)的图象交于点A(1,2)和B(-2,a),与y轴交于点M.
(1)、求∠C的度数;(2)、求两颗银杏树B、C之间的距离(结果保留根号).23. 如图,一次函数 =k x + b (k≠0)与反比例函数 (m≠0)的图象交于点A(1,2)和B(-2,a),与y轴交于点M. (1)、求一次函数和反比例函数的解析式;(2)、在y轴上取一点N,当△AMN的面积为3时,求点N的坐标;(3)、将直线 向下平移2个单位后得到直线y3 , 当函数值 时,求x的取值范围.24. 如图,⊙O的半径为1,点A是⊙O的直径BD延长线上的一点,C为⊙O上的一点,AD=CD,∠A=30°.
(1)、求一次函数和反比例函数的解析式;(2)、在y轴上取一点N,当△AMN的面积为3时,求点N的坐标;(3)、将直线 向下平移2个单位后得到直线y3 , 当函数值 时,求x的取值范围.24. 如图,⊙O的半径为1,点A是⊙O的直径BD延长线上的一点,C为⊙O上的一点,AD=CD,∠A=30°. (1)、求证:直线AC是⊙O的切线;(2)、求△ABC的面积;(3)、点E在 上运动(不与B、D重合),过点C作CE的垂线,与EB的延长线交于点F.
(1)、求证:直线AC是⊙O的切线;(2)、求△ABC的面积;(3)、点E在 上运动(不与B、D重合),过点C作CE的垂线,与EB的延长线交于点F.①当点E运动到与点C关于直径BD对称时,求CF的长;
②当点E运动到什么位置时,CF取到最大值,并求出此时CF的长.
25. 如图,已知二次函数的图象与x轴交于A和B(-3,0)两点,与y轴交于C(0,-3),对称轴为直线 ,直线y=-2x+m经过点A,且与y轴交于点D,与抛物线交于点E,与对称轴交于点F. (1)、求抛物线的解析式和m的值;(2)、在y轴上是否存在点P,使得以D、E、P为顶点的三角形与△AOD相似,若存在,求出点P的坐标;若不存在,试说明理由;(3)、直线y=1上有M、N两点(M在N的左侧),且MN=2,若将线段MN在直线y=1上平移,当它移动到某一位置时,四边形MEFN的周长会达到最小,请求出周长的最小值(结果保留根号).
(1)、求抛物线的解析式和m的值;(2)、在y轴上是否存在点P,使得以D、E、P为顶点的三角形与△AOD相似,若存在,求出点P的坐标;若不存在,试说明理由;(3)、直线y=1上有M、N两点(M在N的左侧),且MN=2,若将线段MN在直线y=1上平移,当它移动到某一位置时,四边形MEFN的周长会达到最小,请求出周长的最小值(结果保留根号).