浙江省宁波市江北区2021年数学中考模拟试卷
试卷更新日期:2021-06-17 类型:中考模拟
一、单选题
-
1. 在-2, ,0, 这四个数中,最大的数是( )A、-2 B、 C、0 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 接种疫苗是防控新冠疫情最有效的手段,截至2021年3月23日,我国各地累计报告接种新冠病毒疫苗8284.6万剂次,这也是人类疫苗接种史上首次启动日报制度.其中8284.6万用科学记数法可表示为( )A、 B、 C、 D、4. 不等式组 的解集在数轴上表示正确的是( )A、
 B、
B、 C、
C、 D、
D、 5. 如图所示的几何体是由4个大小相同的小正方体搭成,其左视图是( )
5. 如图所示的几何体是由4个大小相同的小正方体搭成,其左视图是( )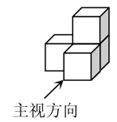 A、
A、 B、
B、 C、
C、 D、
D、 6. 能说明命题“对于任意实数 , ”是假命题的一个反例可以是( )A、 B、 C、 D、7. 从一盒写有“鲜肉3只、蛋黄2只、豆沙2只、排骨3只”的端午粽子(所有粽子的形状大小都一样)礼盒中,随机取出一只粽子,正好是蛋黄粽子的概率是( )A、 B、 C、 D、8. 如图,点 、 、 在⊙O上, , ,则 的度数是( )
6. 能说明命题“对于任意实数 , ”是假命题的一个反例可以是( )A、 B、 C、 D、7. 从一盒写有“鲜肉3只、蛋黄2只、豆沙2只、排骨3只”的端午粽子(所有粽子的形状大小都一样)礼盒中,随机取出一只粽子,正好是蛋黄粽子的概率是( )A、 B、 C、 D、8. 如图,点 、 、 在⊙O上, , ,则 的度数是( )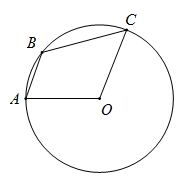 A、110° B、125° C、135° D、165°9. 如图,在菱形 中, , .动点 从点 出发,以每秒2个单位的速度沿折线 运动到点 ,同时动点 也从点 出发,以每秒 个单位的速度沿 运动到点 ,当一个点停止运动时,另一个点也随之停止.设 的面积为 ,运动时间为 秒,则下列图象能大致反映 与 之间函数关系的是( )
A、110° B、125° C、135° D、165°9. 如图,在菱形 中, , .动点 从点 出发,以每秒2个单位的速度沿折线 运动到点 ,同时动点 也从点 出发,以每秒 个单位的速度沿 运动到点 ,当一个点停止运动时,另一个点也随之停止.设 的面积为 ,运动时间为 秒,则下列图象能大致反映 与 之间函数关系的是( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,矩形 ,分别以 、 为边向内作等边三角形(图1);分别以 、 为边向内作等边三角形(图2),两个等边三角形的重叠部分用阴影表示,设图1中阴影部分的面积为 ,图2中阴影部分的面积为 .若 ,则 的值为( )
10. 如图,矩形 ,分别以 、 为边向内作等边三角形(图1);分别以 、 为边向内作等边三角形(图2),两个等边三角形的重叠部分用阴影表示,设图1中阴影部分的面积为 ,图2中阴影部分的面积为 .若 ,则 的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. -3的绝对值等于。12. 二次根式 中字母x的取值范围是 .
13. 将二次函数 的图象向左平移1个单位,再向上平移2个单位后,所得图象的函数表达式为.14. 已知一组数据1, ,5, ,8,10的平均数是6,众数是5,则这组数据的中位数是.15. 如图,⊙O的半径为1,弦 , ,点 为劣弧 上一个动点,延长 至点 ,使 ,当点 由点 运动到点 时,点 的运动路径长为. 16. 如图,直线 与反比例函数 的图象交于点 、 ,与 轴交于点 , 轴于点 , 轴于点 ,点 是线段 的中点,连结 、 ,已知 的面积是 面积的2倍,且 ,则 的值是.
16. 如图,直线 与反比例函数 的图象交于点 、 ,与 轴交于点 , 轴于点 , 轴于点 ,点 是线段 的中点,连结 、 ,已知 的面积是 面积的2倍,且 ,则 的值是.
三、解答题
-
17.(1)、计算:(2)、化简: .
小江的解答如下:
①
②
③
小江的解答过程从第步(填“①”或“②”或“③”)开始出错,请你写出正确的解答过程.
18. 如图,在 的网格中已经涂黑了三个小正方形,请按下列要求画图. (1)、在图1中涂黑一块小正方形,使涂黑的四个小正方形组成一个轴对称图形.(2)、在图2中涂黑一块小正方形,使涂黑的四个小正方形组成一个中心对称图形.19. 某校春日郊游就“最想去的宁波市江北区旅游景点”,随机调查了本校2000名学生中的部分学生,提供四个景点选择:A.达人村;B.慈城古镇;C.保国寺;D.荪湖.要求每位学生选择一个最想去的景点.下面是根据调查结果进行数据整理后绘制的统计图.
(1)、在图1中涂黑一块小正方形,使涂黑的四个小正方形组成一个轴对称图形.(2)、在图2中涂黑一块小正方形,使涂黑的四个小正方形组成一个中心对称图形.19. 某校春日郊游就“最想去的宁波市江北区旅游景点”,随机调查了本校2000名学生中的部分学生,提供四个景点选择:A.达人村;B.慈城古镇;C.保国寺;D.荪湖.要求每位学生选择一个最想去的景点.下面是根据调查结果进行数据整理后绘制的统计图.
请根据图中提供的信息,解答下列问题:
(1)、本次一共随机调查了学生名.(2)、请补全条形统计图.(3)、请估计全校“最想去景点D(荪湖)”的学生人数.20. 如图,已知二次函数 的图象经过点 与点 ,且与 轴交于点 、 . (1)、求该二次函数的表达式,以及与 轴的交点坐标.(2)、若点 在该二次函数图象上,
(1)、求该二次函数的表达式,以及与 轴的交点坐标.(2)、若点 在该二次函数图象上,①求 的最小值;
②若点 到 轴的距离小于3,请结合函数图象直接写出 的取值范围.
21. 如图,机器上使用的螺丝钉,它上面的螺纹以一定的角度旋转上升,使得螺丝旋转时向前推进.一颗底面为圆且直径为6毫米的螺丝钉,如果螺纹的初始角 为4°,那么每转一圈向前推进的距离 约为多少毫米?(参考数据: , , ,结果精确到0.01毫米) 22. 周末傍晚,小北从家出发步行去电影院看电影,出发一段时间后,妈妈发现小北忘了带口罩,于是骑上自行车沿小北行进的路线去追赶,在小北到达电影院之前,妈妈追上小北,然后立即沿原路返程回家,但由于路上行人渐多,妈妈返回时骑车的速度只有原来的 ,小北继续以原速度步行前往并到达电影院.妈妈与小北之间的距离 (米)与小北从家出发后步行的时间 (分)之间的关系如图所示(假设小北步行与妈妈骑车的过程均视为匀速,妈妈将口罩交给小北耽搁的时间忽略不计).
22. 周末傍晚,小北从家出发步行去电影院看电影,出发一段时间后,妈妈发现小北忘了带口罩,于是骑上自行车沿小北行进的路线去追赶,在小北到达电影院之前,妈妈追上小北,然后立即沿原路返程回家,但由于路上行人渐多,妈妈返回时骑车的速度只有原来的 ,小北继续以原速度步行前往并到达电影院.妈妈与小北之间的距离 (米)与小北从家出发后步行的时间 (分)之间的关系如图所示(假设小北步行与妈妈骑车的过程均视为匀速,妈妈将口罩交给小北耽搁的时间忽略不计). (1)、求小北的步行速度;妈妈追赶小北时的速度.(2)、求出图中点 的坐标,并描述说明其表达的实际意义.23. 图1,点 是 内的一点,连结 、 , ,将 绕点 顺时针旋转得 ,射线 交线段 于点 ,射线 交线段 于点 .
(1)、求小北的步行速度;妈妈追赶小北时的速度.(2)、求出图中点 的坐标,并描述说明其表达的实际意义.23. 图1,点 是 内的一点,连结 、 , ,将 绕点 顺时针旋转得 ,射线 交线段 于点 ,射线 交线段 于点 . (1)、求证: .(2)、如图2,若 ,且 , ,求四边形 周长的最小值.(3)、如图3,若 为等边三角形, , ,求 与 的一边平行时 的长.24. 定义:两个角对应互余,且这两个角的夹边对应相等的两个三角形叫做余等三角形.如图1,在 和 中,若 ,且 ,则 和 是余等三角形.
(1)、求证: .(2)、如图2,若 ,且 , ,求四边形 周长的最小值.(3)、如图3,若 为等边三角形, , ,求 与 的一边平行时 的长.24. 定义:两个角对应互余,且这两个角的夹边对应相等的两个三角形叫做余等三角形.如图1,在 和 中,若 ,且 ,则 和 是余等三角形.


 (1)、如图2,等腰直角 ,其中 , ,点 是 上任意一点(不与点 、 重合),则图中 ▲ 和 ▲ 是余等三角形,并求证: .(2)、如图3,四边形 是⊙O的内接四边形,⊙O的半径为5,且 ,
(1)、如图2,等腰直角 ,其中 , ,点 是 上任意一点(不与点 、 重合),则图中 ▲ 和 ▲ 是余等三角形,并求证: .(2)、如图3,四边形 是⊙O的内接四边形,⊙O的半径为5,且 ,①求证: 和 是余等三角形.
②图4,连结 交 于点 ,连结 , 为 上一点,连结 并延长交 于点 ,若 , ,设 , ,求 关于 的函数关系式.