四川省资阳市雁江区2021年初中学业水平考试及适应性检测数学试卷
试卷更新日期:2021-06-17 类型:中考模拟
一、单选题
-
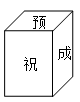
1. ﹣3的绝对值是( )A、﹣3 B、3 C、- D、2. 小明为今年将要参加中考的好友小李制作了一个(如图)正方体礼品盒,六面上各有一字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的平面展开图可能是( )
 A、
A、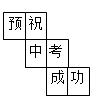 B、
B、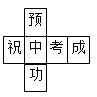 C、
C、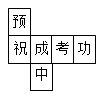 D、
D、 3. 已知某种冠状病毒的直径长约125纳米,1纳米=10﹣9米,那么这种冠状病毒的直径用科学记数法可表示为( )A、125×10﹣9米 B、1.25×10﹣6米 C、1.25×10﹣7米 D、1.25×10﹣8米4. 如图, ,一块含45°角的直角三角板如图放置, ,则 的度数为( )
3. 已知某种冠状病毒的直径长约125纳米,1纳米=10﹣9米,那么这种冠状病毒的直径用科学记数法可表示为( )A、125×10﹣9米 B、1.25×10﹣6米 C、1.25×10﹣7米 D、1.25×10﹣8米4. 如图, ,一块含45°角的直角三角板如图放置, ,则 的度数为( ) A、17° B、27° C、38° D、43°5. 下列计算正确的是( )A、 B、 C、 D、6. 某天 名学生在进入校门时测得体温(单位℃)分别为:36.5 ,36.7 ,36.4 ,36.3,36.4,36.2,36.3,对这组数据描述正确的是( )A、众数是36.4 B、中位数是36.3 C、平均数是36.4 D、方差是1.97. 若关于x的一元二次方程 有实数根,则实数m的取值范围是( )A、 B、 C、 D、8. 如图,在Rt 中, , 为中线,延长 至点E,使 ,连结 ,F为 中点,连结 .若 , ,则 的长为( )
A、17° B、27° C、38° D、43°5. 下列计算正确的是( )A、 B、 C、 D、6. 某天 名学生在进入校门时测得体温(单位℃)分别为:36.5 ,36.7 ,36.4 ,36.3,36.4,36.2,36.3,对这组数据描述正确的是( )A、众数是36.4 B、中位数是36.3 C、平均数是36.4 D、方差是1.97. 若关于x的一元二次方程 有实数根,则实数m的取值范围是( )A、 B、 C、 D、8. 如图,在Rt 中, , 为中线,延长 至点E,使 ,连结 ,F为 中点,连结 .若 , ,则 的长为( )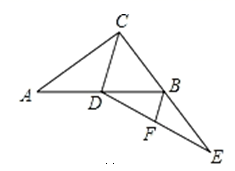 A、2 B、2.5 C、3 D、49. 如图,在扇形纸片 中, 在桌面内的直线l上.现将此扇形在直线l上按顺时针方向旋转(旋转过程中无滑动),当 落在l上时,停止旋转.则点O所经过的路线长为( )
A、2 B、2.5 C、3 D、49. 如图,在扇形纸片 中, 在桌面内的直线l上.现将此扇形在直线l上按顺时针方向旋转(旋转过程中无滑动),当 落在l上时,停止旋转.则点O所经过的路线长为( ) A、 B、 C、 D、10. 如图,抛物线 的顶点和该抛物线与 轴的交点在一次函数 的图象上,它的对称轴是 ,有下列四个结论:① ;② ;③ ;④当 时, ,其中正确的结论是( )
A、 B、 C、 D、10. 如图,抛物线 的顶点和该抛物线与 轴的交点在一次函数 的图象上,它的对称轴是 ,有下列四个结论:① ;② ;③ ;④当 时, ,其中正确的结论是( ) A、①②③ B、①②④ C、①③④ D、①②③④
A、①②③ B、①②④ C、①③④ D、①②③④二、填空题
-
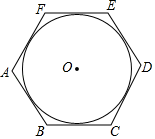
11. 在函数 中,自变量 的取值范围是.12. 若方程x2﹣2x﹣4=0的两个实数根为α,β,则α2+β2的值为 .13. 刘徽是中国古代卓越的数学家之一,他在《九章算术》中提出了“割圆术”,即用圆内接或外切正多边形逐步逼近圆来近似计算圆的面积.下图是其中的一个图形,六边形ABCDEF是⊙O的外切正六边形,现随机向该图形掷一枚小针,则针尖落在⊙O内的概率是 . (结果不取近似值).
 14. 若数 使关于 的不等式组 至少有3个整数解且所有解都是 的解,且使关于 的分式方程 有整数解.则满足条件的所有整数 的和是.15. 如图,把炬形 沿 , 折叠,使点 , 落在 上同一点 处, , 的面积是 , 的面积是 ,则矩形 的面积等于.
14. 若数 使关于 的不等式组 至少有3个整数解且所有解都是 的解,且使关于 的分式方程 有整数解.则满足条件的所有整数 的和是.15. 如图,把炬形 沿 , 折叠,使点 , 落在 上同一点 处, , 的面积是 , 的面积是 ,则矩形 的面积等于.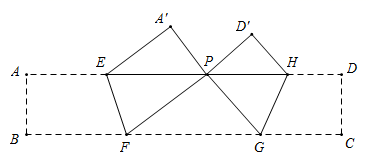 16. 在滑草过程中,小明发现滑道两边形如两条双曲线.如图,点 , , …在反比例函数 的图象上,点 , , …在反比例函数 的图象上, 轴,已知点 , …的横坐标分别为1,2…,令四边形 、 、…的面积分别为 、 、…,(1)用含 的代数式表示 ;(2)若 ,则 .
16. 在滑草过程中,小明发现滑道两边形如两条双曲线.如图,点 , , …在反比例函数 的图象上,点 , , …在反比例函数 的图象上, 轴,已知点 , …的横坐标分别为1,2…,令四边形 、 、…的面积分别为 、 、…,(1)用含 的代数式表示 ;(2)若 ,则 .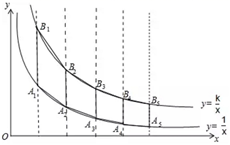
三、解答题
-
17. 先化简再求值:
,其中x是不等式组 的一个整数解.
18. 某学校为了解学生“第二课堂“活动的选修情况,对报名参加A.跆拳道,B.声乐,C.足球,D.古典舞这四项选修活动的学生(每人必选且只能选修一项)进行抽样调查.并根据收集的数据绘制了图①和图②两幅不完整的统计图.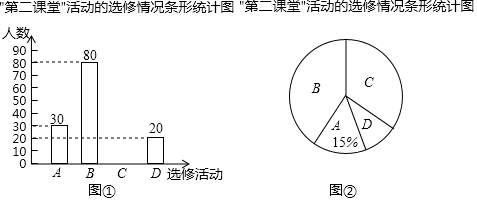
根据图中提供的信息,解答下列问题:
(1)、本次调查的学生共有人;在扇形统计图中,B所对应的扇形的圆心角的度数是;(2)、将条形统计图补充完整;(3)、在被调查选修古典舞的学生中有4名团员,其中有1名男生和3名女生,学校想从这4人中任选2人进行古典舞表演.请用列表或画树状图的方法求被选中的2人恰好是1男1女的概率.19. 如图,圆O是 的外接圆,其切线 与直径 的延长线相交于点E,且 .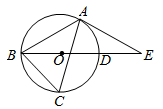 (1)、求 的度数;(2)、若 ,求圆O的半径.20. 由于受到手机更新换代的影响,某手机店经销的华为Mate30手机二月份每台售价比一月份每台售价低500元.如果卖出相同数量的华为Mate30手机,那么一月份销售额为9万元,二月份销售额只有8万元.(1)、一月份Mate30手机每台售价为多少元?(2)、为了提高利润,该店计划三月份购进华为Mate40手机销售,已知华为Mate30每台进价为3500元,华为Mate40每台进价为4000元,预计用不少于7.4万元且不多于7.6万元的资金购进这两种手机共20台,请问有几种进货方案?(3)、该店计划4月份对华为Mate30的尾货进行销售,决定在二月份售价基础上每售出一台华为Mate30手机再返还顾客现金 元,而华为Mate40按销售价4400元销售,如要使(2)中所有方案获利相同, 应取何值?21. 如图,双曲线 与直线 交于 、 两点,点 在双曲线 上,且 .
(1)、求 的度数;(2)、若 ,求圆O的半径.20. 由于受到手机更新换代的影响,某手机店经销的华为Mate30手机二月份每台售价比一月份每台售价低500元.如果卖出相同数量的华为Mate30手机,那么一月份销售额为9万元,二月份销售额只有8万元.(1)、一月份Mate30手机每台售价为多少元?(2)、为了提高利润,该店计划三月份购进华为Mate40手机销售,已知华为Mate30每台进价为3500元,华为Mate40每台进价为4000元,预计用不少于7.4万元且不多于7.6万元的资金购进这两种手机共20台,请问有几种进货方案?(3)、该店计划4月份对华为Mate30的尾货进行销售,决定在二月份售价基础上每售出一台华为Mate30手机再返还顾客现金 元,而华为Mate40按销售价4400元销售,如要使(2)中所有方案获利相同, 应取何值?21. 如图,双曲线 与直线 交于 、 两点,点 在双曲线 上,且 .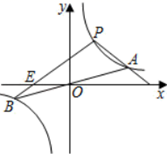 (1)、设 交 轴于点 ,若 ,求点 的坐标;(2)、连接 、 ,得到 ,若 ,求 的面积.22. 江阴芙蓉大道城市快速路在2020年5月份通车,在安装路灯过程中,工人师傅发现垂直于地面的灯柱OA与灯杆AB相交成一定的角度才能产生光照效果,路灯采用锥形灯罩,在地面上的照射区域OC长为8m,从O、C两处测得路灯B的仰角分别为∠BOC和∠BCO,且tan∠BOC=4,tan∠BCO= .
(1)、设 交 轴于点 ,若 ,求点 的坐标;(2)、连接 、 ,得到 ,若 ,求 的面积.22. 江阴芙蓉大道城市快速路在2020年5月份通车,在安装路灯过程中,工人师傅发现垂直于地面的灯柱OA与灯杆AB相交成一定的角度才能产生光照效果,路灯采用锥形灯罩,在地面上的照射区域OC长为8m,从O、C两处测得路灯B的仰角分别为∠BOC和∠BCO,且tan∠BOC=4,tan∠BCO= . (1)、求路灯B到地面的距离;(2)、若∠OAB=120°,求灯柱OA的高度(结果保留根号).23. 如图①,在矩形 中, ,对角线 , 相交于点 , ,点 是线段 上一点,连接 ,将线段 绕点 逆时针旋转 得到线段 ,连接 .
(1)、求路灯B到地面的距离;(2)、若∠OAB=120°,求灯柱OA的高度(结果保留根号).23. 如图①,在矩形 中, ,对角线 , 相交于点 , ,点 是线段 上一点,连接 ,将线段 绕点 逆时针旋转 得到线段 ,连接 . (1)、求证: ;(2)、连接 交 于点 ,求 的最大值;(3)、如图②,点 在射线 上运动,连接 ,在点 的运动过程中,若 ,求 的长.24. 图①,二次函数y=ax2+bx+c(a≠0)的图象经过点A(﹣1,0),并且与直线y= x﹣2相交于坐标轴上的B、C两点,动点P在直线BC下方的二次函数的图象上.
(1)、求证: ;(2)、连接 交 于点 ,求 的最大值;(3)、如图②,点 在射线 上运动,连接 ,在点 的运动过程中,若 ,求 的长.24. 图①,二次函数y=ax2+bx+c(a≠0)的图象经过点A(﹣1,0),并且与直线y= x﹣2相交于坐标轴上的B、C两点,动点P在直线BC下方的二次函数的图象上. (1)、求此二次函数的表达式;(2)、如图①,连接PC,PB,设△PCB的面积为S,求S的最大值;(3)、如图②,抛物线上是否存在点Q,使得∠ABQ=2∠ABC?若存在,则求出直线BQ的解析式及Q点坐标;若不存在,请说明理由.
(1)、求此二次函数的表达式;(2)、如图①,连接PC,PB,设△PCB的面积为S,求S的最大值;(3)、如图②,抛物线上是否存在点Q,使得∠ABQ=2∠ABC?若存在,则求出直线BQ的解析式及Q点坐标;若不存在,请说明理由.