四川省宜宾市江安县2021年数学中考二诊试卷
试卷更新日期:2021-06-17 类型:中考模拟
一、单选题
-
1. 2021的相反数是( )A、 -2021 B、 C、2021 D、2. 如图分别是厨余垃圾,可回收物,有害垃圾,和其他垃圾的标识,其中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 据央广网消息,近年来,数字贸易在国内创造了高达32000亿元的经济效益.将数据“32000亿”用科学记数法表示为( )A、 B、 C、 D、4. 如图是手提水果篮抽象的几何体,则它的俯视图为( )
3. 据央广网消息,近年来,数字贸易在国内创造了高达32000亿元的经济效益.将数据“32000亿”用科学记数法表示为( )A、 B、 C、 D、4. 如图是手提水果篮抽象的几何体,则它的俯视图为( )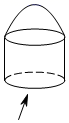 A、
A、 B、
B、 C、
C、 D、
D、 5. 下列运算正确的是( )A、2a+3a=5a2 B、(﹣ab2)3=﹣a3b6 C、a2•a3=a6 D、(a+2b)2=a2+4b26. 某体育用品商店对某一型号运动服9月份的销售情况的统计如图所示,店长决定下个月进该型号运动服时多进一些蓝色的,店长的这一决定主要参考销售数据中的( )
5. 下列运算正确的是( )A、2a+3a=5a2 B、(﹣ab2)3=﹣a3b6 C、a2•a3=a6 D、(a+2b)2=a2+4b26. 某体育用品商店对某一型号运动服9月份的销售情况的统计如图所示,店长决定下个月进该型号运动服时多进一些蓝色的,店长的这一决定主要参考销售数据中的( ) A、平均数 B、方差 C、中位数 D、众数7. 如图,圆锥形的烟囱冒的底面直径是 ,母线长是 ,制作100个这样的烟囱冒至少需要铁皮( )
A、平均数 B、方差 C、中位数 D、众数7. 如图,圆锥形的烟囱冒的底面直径是 ,母线长是 ,制作100个这样的烟囱冒至少需要铁皮( )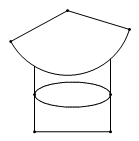 A、 B、 C、 D、8. 如图,在 中, 的垂直平分线 交 于点D,交 于点E,连接 ,若 ,则 的面积为( )
A、 B、 C、 D、8. 如图,在 中, 的垂直平分线 交 于点D,交 于点E,连接 ,若 ,则 的面积为( )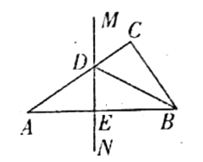 A、16 B、32 C、48 D、649. “新冠”疫情中,某呼吸机厂家接到一份生产300台呼吸机的订单,在生产完成一半时,应客户要求,需提前供货,每天比原来多生产20台呼吸机,结果提前2天完成任务.设原来每天生产x台呼吸机,下列列出的方程中正确的是( )A、 B、 C、 D、10. 若关于x的一元一次不等式结 的解集为 ;且关于 的分式方程 有正整数解,则所有满足条件的整数a的值之积是( )A、7 B、-14 C、28 D、-5611. 如图,在边长为12的正方形 中,E是 上一点, ,且 ,则 ( )
A、16 B、32 C、48 D、649. “新冠”疫情中,某呼吸机厂家接到一份生产300台呼吸机的订单,在生产完成一半时,应客户要求,需提前供货,每天比原来多生产20台呼吸机,结果提前2天完成任务.设原来每天生产x台呼吸机,下列列出的方程中正确的是( )A、 B、 C、 D、10. 若关于x的一元一次不等式结 的解集为 ;且关于 的分式方程 有正整数解,则所有满足条件的整数a的值之积是( )A、7 B、-14 C、28 D、-5611. 如图,在边长为12的正方形 中,E是 上一点, ,且 ,则 ( )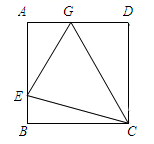 A、8 B、10 C、12 D、1612. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
A、8 B、10 C、12 D、1612. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( ) A、
A、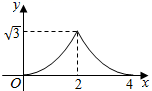 B、
B、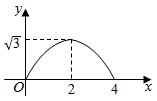 C、
C、 D、
D、
二、填空题
-
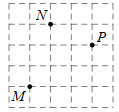
13. 分解因式: .14. 如图,某小区有古树 棵,分别记作为 若建立平面直角坐标系,将古树 用坐标分别表示为 和 ,则古树 用坐标表示为
 15. 如图,直线 ,直线 分别交 于 两点, 平分 ,若 ,则 .
15. 如图,直线 ,直线 分别交 于 两点, 平分 ,若 ,则 .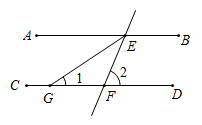 16. 在“抗疫”期间,某药店计划一次购进 两种型号的口罩共200盒,每盒A型口罩的销售利润为7.5元,每盒B型口罩的销售利润为10元,若要求B型口罩的进货量不超过A型口罩的3倍,且完全售出后利润不少于1870元,则该药店在此次进货中获得的最大利润是元.17. 如图,在△ABC中,AB>AC,∠B=45°,AC=5,BC=4 ;E是AB边上一点,将△BEC沿EC所在直线翻折得到△DEC,DC交AB于F,当DE∥AC时,tan∠DCE的值为.
16. 在“抗疫”期间,某药店计划一次购进 两种型号的口罩共200盒,每盒A型口罩的销售利润为7.5元,每盒B型口罩的销售利润为10元,若要求B型口罩的进货量不超过A型口罩的3倍,且完全售出后利润不少于1870元,则该药店在此次进货中获得的最大利润是元.17. 如图,在△ABC中,AB>AC,∠B=45°,AC=5,BC=4 ;E是AB边上一点,将△BEC沿EC所在直线翻折得到△DEC,DC交AB于F,当DE∥AC时,tan∠DCE的值为.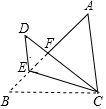 18. 如图,在矩形 中, 的平分线交 于点 于点H,连接 并延长交 于点F,连接 交 于点O.下列结论:① ;② ;③H为 的中点;④ .其中正确的有(将所有正确结论的序号填在横线上)
18. 如图,在矩形 中, 的平分线交 于点 于点H,连接 并延长交 于点F,连接 交 于点O.下列结论:① ;② ;③H为 的中点;④ .其中正确的有(将所有正确结论的序号填在横线上)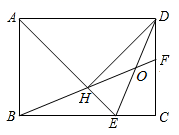
三、解答题
-
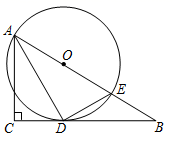
19.(1)、计算: .(2)、先化简,再求值: ,其中 .20. 如图,在四边形 中, ∠A=90°,对角线 平分 ,且 于点 .
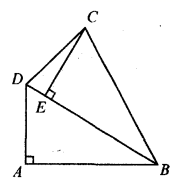 (1)、求证: .(2)、当时 ,求 的度数.21. “学而时习之,不亦说乎?”古人把经常复习当作是一种乐趣.某校为了解九年级(一)班学生每周的复习情况,班长对该班学生每周的复习时间进行了调查,复习时间四舍五入后只有4种:1小时,2小时,3小时,4小时,已知该班共有50人,根据调查结果,制作了两幅不完整的统计图表,该班女生一周的复习时间数据(单位:小时)如下:1,1,1,2,2,2,2,2,2,2,3,3,3,3,4,4,4,4,4,4
(1)、求证: .(2)、当时 ,求 的度数.21. “学而时习之,不亦说乎?”古人把经常复习当作是一种乐趣.某校为了解九年级(一)班学生每周的复习情况,班长对该班学生每周的复习时间进行了调查,复习时间四舍五入后只有4种:1小时,2小时,3小时,4小时,已知该班共有50人,根据调查结果,制作了两幅不完整的统计图表,该班女生一周的复习时间数据(单位:小时)如下:1,1,1,2,2,2,2,2,2,2,3,3,3,3,4,4,4,4,4,4九年级(一)班女生一周复习时间频数分布表:
复习时间
频数(学生人数)
1小时
3
2小时
a
3小时
4
4小时
6
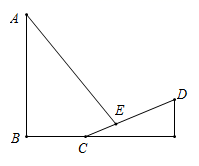
(1)、统计表中a= , 该班女生一周复习时间的中位数为小时;(2)、扇形统计图中,该班男生一周复习时间为4小时所对应圆心角的度数为°; (3)、该校九年级共有600名学生,通过计算估计一周复习时间为4小时的学生有多少名?(4)、在该班复习时间为4小时的女生中,选择其中四名分别记为A,B,C,D,为了培养更多学生对复习的兴趣,随机从该四名女生中选取两名进行班会演讲,请用树状图或者列表法求恰好选中B和D的概率.22. 周末时,小明和妈妈在小区对面的山上玩,回家走到E点时,在E点处测得楼顶A的仰角为 ,沿着坡度 的山坡向下走了13米达到C处,再往前走了42米达到了B处,求小明家所住楼房的高度.(精确到米)
(3)、该校九年级共有600名学生,通过计算估计一周复习时间为4小时的学生有多少名?(4)、在该班复习时间为4小时的女生中,选择其中四名分别记为A,B,C,D,为了培养更多学生对复习的兴趣,随机从该四名女生中选取两名进行班会演讲,请用树状图或者列表法求恰好选中B和D的概率.22. 周末时,小明和妈妈在小区对面的山上玩,回家走到E点时,在E点处测得楼顶A的仰角为 ,沿着坡度 的山坡向下走了13米达到C处,再往前走了42米达到了B处,求小明家所住楼房的高度.(精确到米)(参考数据: )
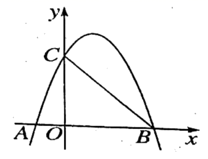
 23. 如图所示,直线 与反比例函数 的图象交于点 ,点 是反比例函数图象上一点,且 .
23. 如图所示,直线 与反比例函数 的图象交于点 ,点 是反比例函数图象上一点,且 .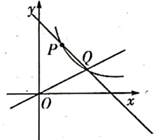 (1)、求反比例函数和直线 的解析式;(2)、若点M在x轴上,使得 的面积为3,求点M的坐标.
(1)、求反比例函数和直线 的解析式;(2)、若点M在x轴上,使得 的面积为3,求点M的坐标.