四川省成都市高新区2021年数学中考二诊试卷
试卷更新日期:2021-06-17 类型:中考模拟
一、单选题
-
1. ﹣ 的相反数是( )A、﹣5 B、5 C、﹣ D、2. 2020年11月24日22时6分,嫦娥五号实现了飞行过程中第一次轨道修正后继续飞向月球.截止当时,嫦娥五号距离地球约160000公里( )A、 B、 C、 D、3. 抽样调查了某年级30名女生所穿鞋子的尺码,数据如下(单位:码)
号码
33
34
35
36
37
人数
7
9
12
1
1
那么这30名女生所穿鞋子的尺码的中位数、众数分别是( )
A、34,35 B、34.5,35 C、35,35 D、35,374. 某鱼塘里养了1600条鲤鱼,若干条草鱼和800条鲢鱼,该鱼塘主通过多次捕捞试验后发现,捕到草鱼的频率稳定在0.5附近,则该鱼塘捞到鲢鱼的概率约为( )A、 B、 C、 D、5. 如图,晚上小明在路灯下沿路从 处径直走到 处,这一过程中他在地上的影子( )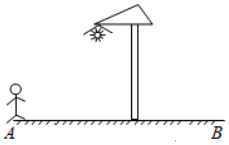 A、一直都在变短 B、先变短后变长 C、一直都在变长 D、先变长后变短6. 已知点 是反比例函数 图象上的两点,则( )A、 B、 C、 D、7. 三角形在正方形网格纸中的位置如图所示,则sinα的值是( )
A、一直都在变短 B、先变短后变长 C、一直都在变长 D、先变长后变短6. 已知点 是反比例函数 图象上的两点,则( )A、 B、 C、 D、7. 三角形在正方形网格纸中的位置如图所示,则sinα的值是( )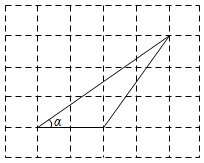 A、 B、 C、 D、8. 如图,在正方形ABCD中,E为AB中点,连结DE,过点D作 交BC的延长线于点F,连结 若 ,则EF的值为
A、 B、 C、 D、8. 如图,在正方形ABCD中,E为AB中点,连结DE,过点D作 交BC的延长线于点F,连结 若 ,则EF的值为 A、3 B、 C、 D、49. 如图,AB为⊙O的直径,点C,D在圆上,若∠D=65°,则∠BAC=( )
A、3 B、 C、 D、49. 如图,AB为⊙O的直径,点C,D在圆上,若∠D=65°,则∠BAC=( ) A、20° B、25° C、30° D、35°10. 将抛物线y=3x2+2向左平移2个单位长度,再向下平移3个单位长度,则得到的抛物线的解析式为( )A、y=3(x﹣2)2﹣1 B、y=3(x﹣2)2+5 C、y=3(x+2)2﹣1 D、y=3(x+2)2+5
A、20° B、25° C、30° D、35°10. 将抛物线y=3x2+2向左平移2个单位长度,再向下平移3个单位长度,则得到的抛物线的解析式为( )A、y=3(x﹣2)2﹣1 B、y=3(x﹣2)2+5 C、y=3(x+2)2﹣1 D、y=3(x+2)2+5二、填空题
-
11. 正n边形的一个外角的度数为60°,则n的值为 .12. 在比例尺为 的某市旅游地图上,某条道路的长为 ,则这条道路的实际长度为 .13. 关于 的方程 有两个实数根,则 的取值范围是.14. 如图,直线 ,直线 分别与 ,PQ交于点A,B,小宇同学利用尺规按以下步骤作图:①以点 为圆心,以任意长为半径作弧交 于点 ,交AB于点 ,②分别以C、D为圆心,以大于 长为半径作弧,两弧在 内交于点 ;③作射线 交 于点F,若∠ABP=70°,则 .
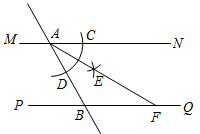 15. 若关于 的一元二次方程 有两个相等的实数根,则 .16. 已知线段AB=2cm,点C在线段AB上,且AC2=BC·AB , 则AC的长cm.17. 如图,在平面直角坐标系 中,等边 的顶点 在 轴的正半轴上, , ,点 ,将 绕点 顺时针旋转60°得到 ,则 的长度为 , 图中阴影部分面积为.
15. 若关于 的一元二次方程 有两个相等的实数根,则 .16. 已知线段AB=2cm,点C在线段AB上,且AC2=BC·AB , 则AC的长cm.17. 如图,在平面直角坐标系 中,等边 的顶点 在 轴的正半轴上, , ,点 ,将 绕点 顺时针旋转60°得到 ,则 的长度为 , 图中阴影部分面积为. 18. 如图,一次函数 与反比例函数 的图象在第一象限交于点A,点C在以 为圆心,1为半径的⊙B上,已知当点C到直线OA的距离最大时 的面积为8,则该反比例函数的表达式为.
18. 如图,一次函数 与反比例函数 的图象在第一象限交于点A,点C在以 为圆心,1为半径的⊙B上,已知当点C到直线OA的距离最大时 的面积为8,则该反比例函数的表达式为. 19. 如图,面积为4的平行四边形 中, ,过点 作 边的垂线,垂足为点 ,点 正好是 的中点,点 、点 分别是 、 .上的动点, 的延长线交线段 于点 ,若点 是唯一使得线段 的点,则线段 长 的取值范围是.
19. 如图,面积为4的平行四边形 中, ,过点 作 边的垂线,垂足为点 ,点 正好是 的中点,点 、点 分别是 、 .上的动点, 的延长线交线段 于点 ,若点 是唯一使得线段 的点,则线段 长 的取值范围是.
三、解答题
-
20.(1)、计算: +(﹣1)0﹣2sin45°;(2)、化简: .21. 解不等式组: 并在数轴上表示出不等式组的解集
 22. 学习习近平总书记关于生态文明建设重要讲话,牢固树立“绿水青山就是金山银山”的科学观,让环保理念深入到学校,某校张老师为了了解本班学生3月植树成活情况,对本班全体学生进行了调查,并将调查结果分为了三类:A:好,B:中,C:差.请根据图中信息,解答下列问题:
22. 学习习近平总书记关于生态文明建设重要讲话,牢固树立“绿水青山就是金山银山”的科学观,让环保理念深入到学校,某校张老师为了了解本班学生3月植树成活情况,对本班全体学生进行了调查,并将调查结果分为了三类:A:好,B:中,C:差.请根据图中信息,解答下列问题: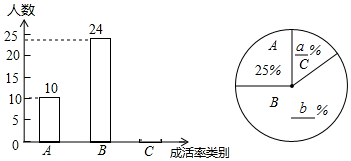 (1)、求全班学生总人数;(2)、在扇形统计图中,a= , b= , C类的圆心角为;(3)、张老师在班上随机抽取了4名学生,其中A类1人,B类2人,C类1人,若再从这4人中随机抽取2人,请求出全是B类学生的概率.23. 浮式起重机是海上打捞、海上救援和海上装卸的重要设备(如图①),某公司的浮式起重机需更换悬索,该公司设计了一个数学模型(如图(2),测量知, , , .请你利用以上数据,求出悬索 和支架 的长(结果取整数).参考数据: , , , .
(1)、求全班学生总人数;(2)、在扇形统计图中,a= , b= , C类的圆心角为;(3)、张老师在班上随机抽取了4名学生,其中A类1人,B类2人,C类1人,若再从这4人中随机抽取2人,请求出全是B类学生的概率.23. 浮式起重机是海上打捞、海上救援和海上装卸的重要设备(如图①),某公司的浮式起重机需更换悬索,该公司设计了一个数学模型(如图(2),测量知, , , .请你利用以上数据,求出悬索 和支架 的长(结果取整数).参考数据: , , , . 24. 如图,在平面直角坐标系中,菱形 的顶点 与原点 重合,点D在反比例函数 ( , )的图象上, ,设 所在直线解析式为 ( ).
24. 如图,在平面直角坐标系中,菱形 的顶点 与原点 重合,点D在反比例函数 ( , )的图象上, ,设 所在直线解析式为 ( ). (1)、求 的值;(2)、若将菱形 沿 轴正方向平移 个单位,在平移中,若反比例函数图象与菱形的边 始终有交点,求 的取值范围.25. 如图,在 中, , 的角平分线交 于点 ,点 是 上一点,以 为直径的 分别交 、 于点 、 .
(1)、求 的值;(2)、若将菱形 沿 轴正方向平移 个单位,在平移中,若反比例函数图象与菱形的边 始终有交点,求 的取值范围.25. 如图,在 中, , 的角平分线交 于点 ,点 是 上一点,以 为直径的 分别交 、 于点 、 . (1)、求证: 是 的切线;(2)、 ,求 ;(3)、在(2)问的条件下,点 为 上一点,过点 作 的垂线,交 延长线于点 ,交 于点 , .若 的半径为5,求 的长.26. 某超市销售一款“免洗洗手液”,这款“免洗洗手液”的成本价为每瓶16元,当销售单价定为20元时,每天可售出80瓶,现决定降价销售.市场调查反映:销售单价每降低0.5元,则每天可多售出20瓶(销售单价不低于成本价)(元),每天的销售量为 (瓶).(1)、求每天的销售量 (瓶)与销售单价 (元)之间的函数关系式;(2)、当销售单价为多少元时,销售这款“免洗洗手液”每天的销售利润最大,最大利润为多少元?27. 正方形 中, 、 分别是 、 上的动点,且 , 与 交于点 .
(1)、求证: 是 的切线;(2)、 ,求 ;(3)、在(2)问的条件下,点 为 上一点,过点 作 的垂线,交 延长线于点 ,交 于点 , .若 的半径为5,求 的长.26. 某超市销售一款“免洗洗手液”,这款“免洗洗手液”的成本价为每瓶16元,当销售单价定为20元时,每天可售出80瓶,现决定降价销售.市场调查反映:销售单价每降低0.5元,则每天可多售出20瓶(销售单价不低于成本价)(元),每天的销售量为 (瓶).(1)、求每天的销售量 (瓶)与销售单价 (元)之间的函数关系式;(2)、当销售单价为多少元时,销售这款“免洗洗手液”每天的销售利润最大,最大利润为多少元?27. 正方形 中, 、 分别是 、 上的动点,且 , 与 交于点 .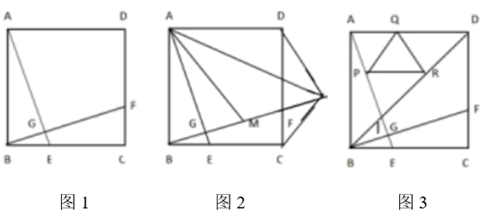 (1)、如图1,若 , ,求 ;(2)、如图2,在 上截取 , 的平分线交 于点 ,连接 ,求证: .(3)、如图3,若 ,在 上截取 ,点 、 分别是 、 上的动点,直接写出 的周长的最小值.28. 如图,在平面直角坐标系中,抛物线 ( )与 轴交于点 、 ,与 轴交于点 ,且 ,点 是第一象限内抛物线上的动点.
(1)、如图1,若 , ,求 ;(2)、如图2,在 上截取 , 的平分线交 于点 ,连接 ,求证: .(3)、如图3,若 ,在 上截取 ,点 、 分别是 、 上的动点,直接写出 的周长的最小值.28. 如图,在平面直角坐标系中,抛物线 ( )与 轴交于点 、 ,与 轴交于点 ,且 ,点 是第一象限内抛物线上的动点. (1)、求抛物线的解析式;(2)、连接 与 ,交于点 ,当 的值最大时,求点 的坐标;(3)、点 在抛物线上运动,点 在 轴上运动,是否存在点 、点 .使 ,且 与 相似,若存在,请求出点 、点 的坐标.
(1)、求抛物线的解析式;(2)、连接 与 ,交于点 ,当 的值最大时,求点 的坐标;(3)、点 在抛物线上运动,点 在 轴上运动,是否存在点 、点 .使 ,且 与 相似,若存在,请求出点 、点 的坐标.