江苏省泰州市海陵区2021年数学中考一模试卷

试卷更新日期：2021-06-17 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣3的绝对值是（）

A、﹣3 B、3 C、- $\frac{1}{3}$ D、 $\frac{1}{3}$

查看试题解析
2. 下列计算正确的是（）

A、 ${(a^{3})}^{2} = a^{5}$ B、 ${(a - 1)}^{2} = a^{2} - 1$ C、 $a^{2} \cdot a^{3} = a^{5}$ D、 $2 a^{2} + a^{2} = 3 a^{4}$

查看试题解析
3. 根据泰州市统计局2021年3月15日公布的数据，2020年全市实现地区生产总值约531300000000元，比上年增长3.6%.将531300000000用科学记数法表示为（）

A、 $5.313 \times 10^{12}$ B、 $5.313 \times 10^{11}$ C、 $53.13 \times 10^{11}$ D、 $53.13 \times 10^{10}$

查看试题解析
4. 一组数据8，7，3，8，12的众数是（）

A、7 B、3 C、12 D、8

查看试题解析
5. 已知点 $P (m ， n)$ 是一次函数 $y = - 2 x + 1$ 图象上任意一点，则 $2 m + n$ 的值等于（）

A、1 B、-1 C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
6. 一个适当大的正六边形，它的一个顶点与一个边长为定值的小正六边形 $A B C D E F$ 的中心 $O$ 重合，且与边 $A B$ 、 $C D$ 相交于 $G$ 、 $H$ （如图）.图中阴影部分的面积记为 $S$ ，三条线段 $G B$ 、 $B C$ 、 $C H$ 的长度之和记为 $l$ ，在大正六边形绕点 $O$ 旋转过程中，下列说法正确的是（）

A、 $S$ 变化， $l$ 不变 B、 $S$ 不变， $l$ 变化 C、 $S$ 变化， $l$ 变化 D、 $S$ 与 $l$ 均不变

查看试题解析

二、填空题

7. 化简： $\sqrt{\frac{2}{5}}$ =

查看试题解析
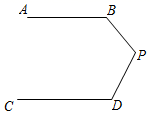
8. 若二次根式 $\sqrt{x + 4}$ 有意义.则x的取值范围是.

查看试题解析
9. 当气温与人体正常体温（37℃）之比等于黄金分割比0.618时，人体感觉最舒适，这个气温约为℃.（取整数）

查看试题解析
10. 将一次函数 $y = 3 x + 2$ 的图象向下平移3个单位，则平移后一次函数的图象与 $y$ 轴的交点坐标是.

查看试题解析
11. 如图，AB∥CD，则∠B+∠D+∠P＝．

查看试题解析
12. 如图， $A$ 、 $B$ 、 $C$ 、 $D$ 是 $⊙ O$ 上四点， $C$ 为 $\overset{⌢}{B D}$ 的中点，如果 $∠ A = 25 °$ ，则 $∠ C B D$ 的度数为°.

查看试题解析
13. 已知 $y = \frac{1}{3} [{(x - 1)}^{2} + {(x - 3)}^{2} + {(x - 2)}^{2}]$ ，当 $x =$ 时， $y$ 的值最小.

查看试题解析
14. 如图，一个圆锥的底面圆半径 $O A = 5 cm$ ，将其侧面沿一条母线剪开展成一个扇形，若该扇形恰好是半圆，则这个半圆的面积等于 ${cm}^{2}$ （结果保留 $π$ ）

查看试题解析
15. 如图，已知面积等于16的正方形 $A B C D$ 的两个顶点 $B$ 、 $D$ 是反比例函数 $y = \frac{k}{x} (k > 0 ， x > 0)$ 的图象上两点，若点 $D$ 坐标是 $(m ， n)$ ，则 $m - n$ 的值等于.

查看试题解析
16. 已知二次函数 $y = a x^{2} + b x + c$ 的图象经过点 $(3 ， 0)$ 与 $(- 1 ， 0)$ ，关于 $x$ 的方程 $a x^{2} + b x + c + m = 0 (m > 0)$ 有两个根，其中一个根是5，若关于 $x$ 的方程 $a x^{2} + b x + c + n = 0 (0 < n < m)$ 有两个整数根，则这两个整数根分别是.

查看试题解析

三、解答题

17.

(1)、计算： $\sqrt{2} \sin 45 ° + {(\frac{1}{4})}^{- 2} + {(- 2)}^{3}$ ；

(2)、解不等式组 ${\begin{array}{l} 2 x - 7 \leq x + 2, \\ \frac{x + 2}{4} - \frac{x}{6} > 1. \end{array}$ ，并写出不等式组的正整数解.

查看试题解析
18. 为有效控制新型冠状病毒的传染，目前，国家正全面推开新冠疫苗的免费接种工作.某社区为了解其辖区内居民的接种情况，随机抽查了一部分居民进行问卷调查，把调查的结果分为 $A$ （已经接种）、 $B$ （准备接种）、 $C$ （观望中）、 $D$ （不接种）四种类别，并绘制了下面两幅不完整的统计图，请根据图中提供的信息解答下列问题：

(1)、此次抽查的居民人数为人；

(2)、请补全条形统计图，同时求出 $C$ 类别所在扇形的圆心角度数；

(3)、若该社区共有居民4000人，请你估计该社区已接种新冠疫苗的居民约有多少人？

查看试题解析
19. 为打赢脱贫攻坚战，全面奔向小康社会，某市科技人员带着 $A$ 、 $B$ 、 $C$ 三个扶贫项目来到某村，对甲、乙两个贫困户进行帮扶，贫困户可从中随机选择一个项目.

(1)、甲贫困户恰好选择 $A$ 扶贫项目的概率是；

(2)、甲、乙两个贫困户恰好选择相同项目的概率是多少？（请用树状图或列表进行解答）

查看试题解析
20. 如图

(1)、如图1，在 $▱ A B C D$ 中，点 $E$ 、 $F$ 分别在 $B C$ 、 $A D$ 上，且线段 $E F$ 经过对角线 $A C$ 的中点 $O$ .求证： $O E = O F$ ；

(2)、如图2，在 $▱ A B C D$ 中，点 $E$ 、 $F$ 分别在 $C D$ 、 $A D$ 上，试仅用一把无刻度的直尺画出 $▱ E F G H$ ，使得 $G$ 、 $H$ 分别在边 $A B$ 、 $B C$ 上，并写出作图步骤（保留作图痕迹）.

查看试题解析
21. 已知：如图，在⊙O中，弦 $A B$ 与 $C D$ 相交于点 $E$ ， $∠ A C D = 60 °$ ，给出下列信息：

① $∠ A D C = 50 °$ ；② $A B$ 是⊙O的直径；③ $∠ C E B = 100 °$ .

(1)、请在上述3条信息中选择其中两条作为条件，剩下的一条作为结论.你选择的条件是 ▲ ，结论是 ▲ （只要填写序号）.判断此命题是否正确，并说明理由；

(2)、在（1）的情况下，若 $A D = 2 \sqrt{3}$ ，求 $\overset{⌢}{A D}$ 的长度.

查看试题解析
22. 为配制一定浓度的盐水溶液，在一个足够大的容器中，先加入 $10 g$ 的盐和一定量的水.由于实验的需要发现盐水质量不够，又加入 $5 g$ 的盐和 $40 g$ 的水，恰好与原来配制的浓度相同，求原来盐水溶液的质量.

查看试题解析
23. 某校数学兴趣小组为了测量建筑物 $C D$ 的高度，先在斜坡 $A B$ 的底部 $A$ 测得建筑物顶点 $C$ 的仰角为31°，再沿斜坡 $A B$ 走了 $26 m$ 到达斜坡顶点 $B$ 处，然后在点 $B$ 测得建筑物顶点 $C$ 的仰角为53°，已知斜坡 $A B$ 的坡度 $i = 1 ： 2.4$ .（参考数据： $\tan 53 ° \approx \frac{4}{3}$ ， $\tan 31 ° \approx \frac{3}{5}$ ）

(1)、求点 $B$ 到地面的高度；

(2)、求建筑物 $C D$ 的高度.

查看试题解析
24. 在平面直角坐标系中，直线 $y = k x + 2 k (k < 0)$ 与 $x$ 轴交于点 $A$ ，与 $y$ 轴交于点 $P$ ，过点 $A$ 作 $x$ 轴的垂线，交反比例函数 $y = - \frac{8}{x} (x < 0)$ 图象于点 $B$ .

(1)、求点 $A$ 的坐标；

(2)、若四边形 $A B O P$ 为平行四边形，求直线 $y = k x + 2 k$ 的函数关系式；

(3)、在（2）问的条件下，直接写出关于 $x$ 的不等式 $k x + 2 k + 4 + \frac{8}{x} < 0$ 的解集.

查看试题解析
25. 如图，点 $C (0 ， \frac{1}{a}) (a < 0)$ 是 $y$ 轴负半轴上的一点，经过点 $C$ 作直线，与抛物线 $y = a x^{2}$ 交于 $A$ 、 $B$ 两点（点 $A$ 在点 $B$ 的左侧），连接 $O A$ 、 $O B$ ，设点 $A$ 的横坐标为 $m (m < 0)$ .

(1)、若点 $A$ 的坐标为 $(- 4 ， - 2)$ ，求点 $C$ 的坐标；

(2)、若 $A C ： B C = 1 ： 2$ ， $m = - 1$ ，求 $a$ 的值，并证明： $∠ A O B = 90 °$ ；

(3)、若 $A C ： B C = 1 ： k (k > 1)$ ，问“ $∠ A O B = 90 °$ ”这一结论还成立吗？试说明理由.

查看试题解析
26. 已知：如图1，矩形 $A B C D$ 中 $A B = 6$ ， $A D = 12$ ， $O$ 为边 $A D$ 上的一点，以 $O$ 为顶点作 $∠ E O F = 45 °$ ，点 $E$ 在折线段 $A - B - C$ 上，点 $F$ 在折线段 $B - C - D$ 上，点 $E$ 、 $F$ 之间的距离称为 $∠ E O F$ 的“截线长”.

(1)、如图2，若点 $O$ 与点 $A$ 重合，点 $E$ 与点 $B$ 重合时，求 $∠ E O F$ 的“截线长”；

(2)、若点 $O$ 与点 $A$ 重合，点 $F$ 与点 $C$ 重合时，求此时 $∠ E O F$ 的“截线长”；

(3)、若点 $O$ 为 $A D$ 的中点，点 $E$ 在线段 $A B$ 上，当 $∠ E O F$ 的“截线长”为5时，求 $A E$ 的长度.

查看试题解析