江苏省江阴市2021年数学中考一模试卷

试卷更新日期：2021-06-17 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣3的相反数为（）

A、﹣3 B、﹣ $\frac{1}{3}$ C、 $\frac{1}{3}$ D、3

查看试题解析
2. 计算 ${(a^{3})}^{2}$ 的结果是（）

A、 $a^{5}$ B、 $a^{6}$ C、 $a^{8}$ D、 $2 a^{3}$

查看试题解析
3. 函数 $y = \frac{5}{x - 4}$ 中自变量x的取值范围是（）

A、 $x \geq 4$ B、 $x \leq 4$ C、 $x > 4$ D、 $x \neq 4$

查看试题解析
4. 江阴市今年4月上旬有一段时间7天的最高气温为（单位：℃）：20，17，18，20，18，18，22，对这组数据，下列说法正确的是（）

A、平均数为18 B、中位数为20 C、众数为18 D、极差为4

查看试题解析
5. 下列图形中，是中心对称图形但不一定是轴对称图形的是（）

A、等腰三角形 B、平行四边形 C、圆 D、正六边形

查看试题解析
6. 若一个凸多边形的内角和为720°，则这个多边形的边数为 $($ 　　 $)$

A、4 B、5 C、6 D、7

查看试题解析
7. 已知 $⊙ O$ 的圆心O到直线l的距离为5， $⊙ O$ 的半径为3，则直线l和 $⊙ O$ 的位置关系为（）

A、相离 B、相切 C、相交 D、相交或相切

查看试题解析
8. 圆锥的高是 $4cm$ ，其底面圆半径为 $3cm$ ，则它的侧面展开图的面积为（）

A、 ${12πcm}^{2}$ B、 ${24πcm}^{2}$ C、 ${15πcm}^{2}$ D、 ${30πcm}^{2}$

查看试题解析
9. 如图是由一些边长为1的等边三角形组成的网格，其中A、B、D、E均是等边三角形的顶点，延长 $A B$ 交 $D E$ 于点C，则 $\frac{D C}{C E}$ 的值为（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{1}{2}$

查看试题解析
10. 已知如图， $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 90 °$ ，D为线段 $B C$ 上一点，将线段 $A D$ 绕点A逆时针旋转 $90 °$ 得到线段 $A E$ ，F为 $D E$ 中点，直线 $C F$ 交射线 $B A$ 于点G.下列说法：①若连接 $E C$ ，则 $E C ⊥ B C$ ；② $∠ B D A = ∠ E D C$ ；③ $D E = C G$ ；④若 $B D = 2 D C$ ，则 $A D = \sqrt{5} A G$ .其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 分解因式： $m^{2} - 9$ =

查看试题解析
12. 2020年江阴市的国内生产总值（GDP）已经超过4100亿元，数据4100用科学记数法表示为.

查看试题解析
13. 已知 $△ A B C$ 中， $A B = 5$ ， $B C = 6$ ， $A C = 7$ ，点D、E、F分别为三边中点，则 $△ D E F$ 的周长为.

查看试题解析
14. 反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象经过点 $A (- 2 ， 3) ， B (1 ， m)$ ，则m的值为.

查看试题解析
15. 若 $a^{2} + b^{2} = 5$ ， $a + b = 3$ ，则ab的值为.

查看试题解析
16. 请写出一个函数表达式，函数值随自变量的增大而减小：.

查看试题解析

17. 如图1，杆秤是我国传统的计重工具，极大的方便了人们的生活.如图2是杆秤的示意图，可以用秤砣到秤纽的水平距离，来得出秤钩上所挂物体的重量，小明在一次称重时，得到如下一组数据，已知表中有一组数据错了.

秤砣到秤纽的水平距离（cm）	1	2	4	7	12
秤钩所挂物体重量（斤）	0.75	1.00	2.00	2.25	3.50

若秤杆上秤砣到秤纽的水平距离是 $16cm$ ，则秤钩上所挂物体的重量为斤.

查看试题解析

18. 如图，在正方形 $A B C D$ 中， $A B = 4$ ，以B为圆心， $B A$ 长为半径画弧，点E为弧上一点， $E F ⊥ C D$ 于F，连接 $C E$ ，若 $C E - E F = 2$ ，则 $C F$ 的值为.

查看试题解析

三、解答题

19.

(1)、计算： $| - 2 | - {(\frac{1}{3})}^{- 1} + {(π - \sqrt{2021})}^{0}$ ；

(2)、化简： $a - b + \frac{2 b^{2}}{a + b}$ .

查看试题解析
20.

(1)、解方程： $\frac{x}{3} = \frac{x - 2}{2}$ ；

(2)、解不等式组： ${\begin{array}{l} x + 2 (x - 3) < 1 \\ \frac{3 x - 1}{2} \geq 1 \end{array}$

查看试题解析
21. 如图， $▱ A B C D$ 的对角线 $A C$ 、 $B D$ 相交于点O，且 $O E = O F$ .

(1)、求证： $△ B O E ≌ △ D O F$ ；

(2)、求证： $B E / / D F$ .

查看试题解析
22. 无锡有丰富的旅游产品.某校九年级（1）班的同学就部分旅游产品的喜爱情况对部分游客随机调查，要求游客在列举的旅游产品中选出最喜爱的产品，且只能选一项，选项分别为A：酱排骨，B：惠山泥人，C：宜兴紫砂壶，D：油面筋，E：江阴马蹄酥，以下是同学们整理的不完整的统计图：

根据以上信息完成下列问题：

(1)、参与随机调查的游客有人；

(2)、在扇形统计图中，A部分所占的圆心角是 ▲ 度，并将条形统计图补充完整；

(3)、根据调查结果，请估计在20000名游客中，最喜爱江阴马蹄酥的游客约有多少人？

查看试题解析
23. “石头、剪子、布”是一个广为流传的游戏，又称“猜丁壳”，它古老而简单，这个游戏的主要目的是为了解决争议，因为三者相互制约，在不考虑平局的情况下，总会有胜负的时候.一般认为起源于我国，明朝人所写《五杂俎》记载：最早石头、剪子、布起源自汉朝的手势令与豁拳.现有甲、乙两人做“石头、剪子、布”游戏，其规则是：甲、乙两人都做出“石头、剪子、布”3种手势中的一种，其中“石头”胜“剪子”，“剪子”胜“布”，“布”胜“石头”，手势相同不分胜负.假设甲、乙两人每次都随意且同时做出3种手势中的一种.

(1)、乙出剪子的概率为；

(2)、求甲获胜的概率.（请用“画树状图”或“列表”的方法，写出分析过程，并给出结果）

查看试题解析
24. 如图，AB为⊙O的直径，点C，D在⊙O上，且BC＝6 cm，AC＝8 cm，∠ABD＝45°.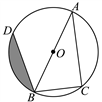

(1)、求BD的长；

(2)、求图中阴影部分的面积．

查看试题解析
25. 如图，一个边长为 $8m$ 的正方形花坛是由4块全等的小正方形区域组成的中心对称图形.在小正方形 $A B C D$ 中，点G、E、F分别在 $C D$ 、 $A B$ 、 $A D$ 上，且 $D G = 1 m ， A E = A F$ .在 $△ A E F$ 、 $△ D F G$ 、五边形 $E B C G F$ 三个区域上种植不同的花卉，每平方米的种植成本分别是20元、20元、10元.问：点E在什么位置时，正方形花坛种植花卉所需的总费用最少，最少为多少元？

查看试题解析
26. 已知二次函数 $y = a x^{2} - 2 a x + c (a < 0)$ 的图象交x轴于点A、B两点（A在B左侧），与y轴交于点C，与其对称轴交于点D，直线BD交y轴于点E，BD=2DE.

(1)、求点A的坐标；

(2)、①连接 $A C ， B C$ ，若 $△ A B C$ 外接圆的圆心正好在x轴上，求二次函数表达式；
②连接 $C D$ ，若 $\tan ∠ C D B = \tan ∠ O B D$ ，求此时二次函数表达式.

查看试题解析
27. 如图

(1)、如图1， $△ A B C$ 中，D为 $A B$ 边上一点，将点A沿经过点D的直线翻折，使得A的对应点 $A^{'}$ 恰好落在 $A C$ 边上，请用无刻度的直尺和圆规作出点 $A^{'}$ ；（不写作法，保留作图痕迹）

(2)、D为线段 $A B$ 中点.
①如图2，点P在线段 $A C$ 上， $P A$ 沿直线 $P D$ 翻折后得到的 $P A^{'} ⊥ A B$ ，请用无刻度的直尺和圆规作出点P；（不写作法，保留作图痕迹）

②如图3， $∠ B A C = 30 °$ ，点P在射线 $A C$ 上， $P A$ 沿直线 $P D$ 翻折后得到的 $P A^{'} ⊥ A B$ ，若 $A B = 4$ ，则线段 $B A^{'}$ 的长度为 ▲ .

查看试题解析
28. 已知，在平面直角坐标系中，点O为坐标原点，点 $A (5 ， 0)$ ，点 $M (m ， 4)$ ，点 $N (m - 5 ， 4)$ ，点P为线段 $A M$ 上一动点.

(1)、求四边形 $O A M N$ 的面积；

(2)、将 $△ O A P$ 沿 $O P$ 翻折得到同一平面内的 $△ O A^{'} P$ （点A的对应点为点 $A^{'}$ ）.
①当点 $A^{'}$ 恰好落在线段 $M N$ 上，求此时m的值或取值范围；

②当点P与点M重合时，记 $△ O A^{'} P$ 与四边形 $O A M N$ 重叠部分的面积为 $S_{1}$ ，四边形 $O A M N$ 的面积为 $S_{2}$ ，若 $\frac{S_{2}}{S_{1}} = \frac{5}{2}$ ，求此时m的值.

查看试题解析