广西来宾市合山市2020-2021学年八年级下学期数学第四次月考试卷
试卷更新日期:2021-06-17 类型:月考试卷
一、选择题(共12小题,每小题3分,共36分。在每小题给出的四个选项中只有一项是符合要求的,用2B铅笔把答题卡上对应题目的答案标号涂黑。)
-
1. 下列四个手机APP图标中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 函数y= 的自变量x的取值范围是( )A、x>-3 B、x≠-3 C、x≥-3 D、x>-3且x≠03. 一组数据共40个,分为6组,第1到第4组的频数分别为10,5,7,6,第5组的频率为0.1,则第6组的频数为( )A、4 B、6 C、8 D、104. 下列四组数据不能作为直角三角形的三边长的是( )A、9,12,15 B、7,24,25 C、15,36,39 D、12,15,205. 如图,将透明直尺叠放在正五边形之上,若正五边形有两个顶点在直尺的边上,且有一边与直尺的边垂直。则∠α=( )
2. 函数y= 的自变量x的取值范围是( )A、x>-3 B、x≠-3 C、x≥-3 D、x>-3且x≠03. 一组数据共40个,分为6组,第1到第4组的频数分别为10,5,7,6,第5组的频率为0.1,则第6组的频数为( )A、4 B、6 C、8 D、104. 下列四组数据不能作为直角三角形的三边长的是( )A、9,12,15 B、7,24,25 C、15,36,39 D、12,15,205. 如图,将透明直尺叠放在正五边形之上,若正五边形有两个顶点在直尺的边上,且有一边与直尺的边垂直。则∠α=( ) A、60° B、28° C、54° D、72°6. 一次函数y=-x+5的图象经过( )A、一、二、三象限 B、一、二、四象限 C、一、三、四象限 D、二、三、四象限7. 如图,矩形 中,对角线 , 交于O点.若 , ,则 的长为( )
A、60° B、28° C、54° D、72°6. 一次函数y=-x+5的图象经过( )A、一、二、三象限 B、一、二、四象限 C、一、三、四象限 D、二、三、四象限7. 如图,矩形 中,对角线 , 交于O点.若 , ,则 的长为( )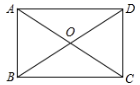 A、4 B、 C、3 D、58. 已知如图,正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=x+k的图象大致是( )A、
A、4 B、 C、3 D、58. 已知如图,正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=x+k的图象大致是( )A、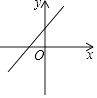 B、
B、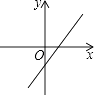 C、
C、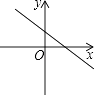 D、
D、 9. 已知甲、乙两地相距s(单位:km),汽车从甲地匀速行驶到乙地,则汽车行驶的时间(单位:h)关于行驶速度v(单位:km/h)的函数图象是( )A、
9. 已知甲、乙两地相距s(单位:km),汽车从甲地匀速行驶到乙地,则汽车行驶的时间(单位:h)关于行驶速度v(单位:km/h)的函数图象是( )A、 B、
B、 C、
C、 D、
D、 10. 将直线y= x+4向下平移5个单位长度,所得直线的表达式为( )A、y= x-1 B、y= x-5 C、y=- x+1 D、y=- x-111. 小文同学统计了某栋居民楼中全体居民每周使用手机支付的次数,并绘制了直方图.根据图中信息,下列说法错误的是( )
10. 将直线y= x+4向下平移5个单位长度,所得直线的表达式为( )A、y= x-1 B、y= x-5 C、y=- x+1 D、y=- x-111. 小文同学统计了某栋居民楼中全体居民每周使用手机支付的次数,并绘制了直方图.根据图中信息,下列说法错误的是( )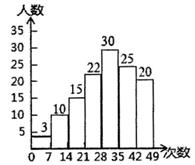 A、这栋居民楼共有居民125人 B、每周使用手机支付次数为28~35次的人数最多 C、有 的人每周使用手机支付的次数在35~42次 D、每周使用手机支付不超过21次的有15人12. 小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发,家到公园的距离为2500m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象。
A、这栋居民楼共有居民125人 B、每周使用手机支付次数为28~35次的人数最多 C、有 的人每周使用手机支付的次数在35~42次 D、每周使用手机支付不超过21次的有15人12. 小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发,家到公园的距离为2500m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象。
①小明所走路程s与时间y的函数关系式为:s=
②小明出发37.5分钟时与爸爸第三次相遇;
③在速度都不变的情况下,小明希望比爸爸早20min到达公园,则小明在步行过程中停留的时间需减少5分钟。
以上说法中,正确的个数有( )
A、1 B、2 C、3 D、0二、填空题(每小题3分,满分18分)
-
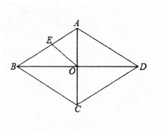
13. P(-3,2)关于x轴对称的点的坐标是14. 当x=时,函数y=2x-3与函数y=-3x+5有相同的函数值。15. 如果一个多边形的每一个外角都等于60°,则它的内角和是.16. 菱形ABCD的两条对角线AC,BD相交于点O,E是AB的中点,若AC=12,菱形ABCD的面积为96,则OE长为。
 17. 已知一次函数y=mx-3的图象与x轴的交点坐标为(x0 , 0),且2≤x0≤3,则m的取值范围是18. 九年级体育测试某班跳绳成绩的频数分布表如下:
17. 已知一次函数y=mx-3的图象与x轴的交点坐标为(x0 , 0),且2≤x0≤3,则m的取值范围是18. 九年级体育测试某班跳绳成绩的频数分布表如下:次数
100≤x<120
120≤x<140
140≤x<160
160≤x<180
180≤x<200
频数
2
3
26
13
6
跳绳次数x在160≤x<180范围的学生占全班学生的(用百分数表示)
三、解答题(共66分)
-
19. 如图所示,在▱ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F,求证:BE=DF.
 20. 如图,AB=BC,∠BAD=∠BCD=90°,点D是EF上一点,AE⊥EF于E,CF⊥EF于F,AE=CF,求证:Rt△ADE≌Rt△CDF
20. 如图,AB=BC,∠BAD=∠BCD=90°,点D是EF上一点,AE⊥EF于E,CF⊥EF于F,AE=CF,求证:Rt△ADE≌Rt△CDF 21. 根据下列条件分别确定函数的解析式:(1)、y与x成正比例,当x=5时,y=6;(2)、直线y=kx+b经过点(3,6)与点(2,-4)22. 如图,已知点A(6,0)、点B(0,-2)。
21. 根据下列条件分别确定函数的解析式:(1)、y与x成正比例,当x=5时,y=6;(2)、直线y=kx+b经过点(3,6)与点(2,-4)22. 如图,已知点A(6,0)、点B(0,-2)。 (1)、求直线AB所对应的函数表达式;(2)、在x轴上找一点P,满足PA=PB,求P点的坐标。23. 已知:如图,△ABC在平面直角坐标系中的位置如图所示
(1)、求直线AB所对应的函数表达式;(2)、在x轴上找一点P,满足PA=PB,求P点的坐标。23. 已知:如图,△ABC在平面直角坐标系中的位置如图所示
( 1 )将△ABC向上平移6个单位得到△A1B1C1 , 请画出△A1B1C1;
( 2 )将△ABC关于y轴对称得到△A2B2C2 , 请画出△A2B2C2;
( 3 )直接写出△ABC的面积 ▲
24. 如图,在正方形ABCD中,E是BC边上的点,连接AE,作BF⊥AE于点O,且点F在CD边上。 (1)、求证:△ABE≌△BCF。(2)、若CE=1,CF=2,求AE的长。25. 2020年,“地摊经济”成为了社会关注的热门话题。小亮从市场得知如下信息:
(1)、求证:△ABE≌△BCF。(2)、若CE=1,CF=2,求AE的长。25. 2020年,“地摊经济”成为了社会关注的热门话题。小亮从市场得知如下信息:甲商品
乙商品
进价(元/件)
35
5
售价(元/件)
45
8
小亮计划购进甲、乙商品共100件进行销售,设小亮购进乙商品x件,甲、乙商品全部销售完后获得利润为y元。
(1)、求出y与x之间的函数关系式。(2)、小亮用不超过2000元资金一次性购进甲、乙两种商品,求x的取值范围。26. 随着社会的发展,私家车变得越来越普及,使用节能低油耗汽车,对环保有着非常积极的意义.某市有关部门对该市的某一型号的若干辆汽车进行了一项油耗抽样试验:在同一条件下,被抽样的该型号汽车,在耗油1L的情况下所行驶的路程(单位:km)。对得到的数据进行统计分析,结果如图所示。
(注:记A为12~12.5,B为12.5~13,C为13~13.5,D为13.5~14,E为14~14.5)
请依据统计结果回答以下问题:
(1)、试求进行该试验的车辆数;(2)、请补全频数直方图;(3)、求扇形D的圆心角的度数。