广西防城区2020-2021学年八年级下学期数学第二次月考试卷
试卷更新日期:2021-06-17 类型:月考试卷
一、单选题(共12小题,每小题3分,共36分)
-
1. 函数y= 中,x的取值范围是( )A、x>-5 B、x>-5且x+0 C、x≥-5且x≠0 D、x≥-5
-
2. ①y=-8x;②y= ;③y= +1;④y=-8x2+6;⑤y=-0.5x-1中,一次函数共有( )A、1个 B、2个 C、3个 D、4个
-
3. 小李骑车沿直线旅行,先前进了1000米,休息了一段时间,又原路返回800米,再前进1200米,则他离起点的距离s与时间t的关系示意图是( )A、
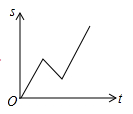 B、
B、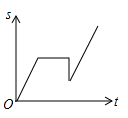 C、
C、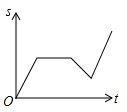 D、
D、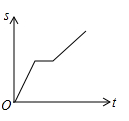
-
4. 下列各图象中,不能表示y是x的函数的是( )A、
 B、
B、 C、
C、 D、
D、
-
5. 一次函数y=3x+6的图象经过( )A、第一、二、三象限 B、第二、三、四象限 C、第一、二、四象限 D、第一、三、四象限
-
6. 直线y=-2x+6与x轴的交点坐标是( )A、(0,-3) B、(0,3) C、(3,0) D、(-3,0)
-
7. 下列关于一次函数y=-2x+2的图象的说法中,错误的是( )A、函数图象经过第一、二、四象限 B、函数图象与x轴的交点坐标为(2,0) C、当x>0时,y<2 D、y的值随着x值的增大而减小
-
8. 若正比例函数y=kx的图象经过点(2,-3),则此图象也必定经过点( )A、(-2,3) B、(2,3) C、(3,-2) D、(-3,-2)
-
9. 如图,直线y=ax+b(a≠0)过点A(0,5),B(-3,0),则方程ax+b>0的解集是( )
 A、x>-3 B、x<-3 C、x>5 D、x>
A、x>-3 B、x<-3 C、x>5 D、x> -
10. 已知直线l:y=kx+k-b与直线y=-2x+1平行,且直线l经过第二,三、四象限,则b的取值范围为( )A、b<-2 B、b<2 C、b>-2 D、b>2
-
11. 一次函数y=mx+n与正比例函数y=mnx(m,n为常数、且mm≠0)在同一平面直角坐标系中的图可能是( )A、
 B、
B、 C、
C、 D、
D、
-
12. A、B两地相距80km,甲、乙两人沿同一条路从A地到B地。I1 , l2分别表示甲、乙两人离开A地的距离s(kxm)与时间t(h)之间的关系。对于以下说法:①乙车出发1.5小时后甲才出发;②两人相遇时,他们离开A地20km;③甲的速度是40km/h,乙的速度是 km/h;④当乙车出发2小时时,两车相距13km。其中正确的结论是( )
 A、①③ B、①④ C、②③ D、②④
A、①③ B、①④ C、②③ D、②④
二、填空题(共6小题,每小题3分,共18分)
-
13. 已知y=(k-3)x|k|-2+2是一次函数,那么k的值为
-
14. 若一次函数y=2x-3的图象经过点A(a,1),则a=
-
15. 把直线y=2x-1向上平移3个单位长度后,所得到的直线对应的函数解析式是
-
16. 如果点P(5,k)在直线y=-2x+3上,那么点P到x轴的距离为
-
17. 如图,平面直角坐标系xOy中,直线y1=k1x+b1的图像与直线y2=k2x+b2的图像相交于点(-1,-3),当y1<y2时,实数x的取值范围为

-
18. 如图,直线y= x+3与坐标轴分别交于点AB,与直线y=x交于点C,Q是线段OA上的动点,连接CQ,若△OQC是等腰三角形,则OQ的长为

三、解答题(共8小题,共66分。需写出完整的解题或推理过程)
-
19. 已知y与x-1成正比例,且当x=3时,y=4。(1)、求出y与x之间的函数解析式;(2)、当x=1时,求y的值。
-
20. 已知:一次函数 的图象经过 , 两点.
 (1)、求一次函数的解析式,并画出此一次函数的图象;(2)、求当x取何值时,函数值 .
(1)、求一次函数的解析式,并画出此一次函数的图象;(2)、求当x取何值时,函数值 . -
21. 一次函数y=kx+b的图象与y=-x平行,且过点A(1,4),求一次函数表达式。
-
22. 已知一次函数y=(2-k)x-k2+4(1)、k为何值时,y随x的增大而减小?(2)、k为何值时,它的图象经过原点?
-
23. 如图,根据一次函数y=kx+b的图象,直接写出下列问题的答案:
 (1)、关于x的方程kx+b=0的解;(2)、当x=1时,代数式k+b的值;(3)、关于x的方程kx+b=-3的解。
(1)、关于x的方程kx+b=0的解;(2)、当x=1时,代数式k+b的值;(3)、关于x的方程kx+b=-3的解。 -
24. 如图,在平面直角坐标系xOy中,已知A(5,-2),B(1,6),直线AB与直线l:y=x+2交于点C,直线l与x轴交于点D。
 (1)、求直线AB的解析式:(2)、求点C的坐标;(3)、求△ACD的面积.
(1)、求直线AB的解析式:(2)、求点C的坐标;(3)、求△ACD的面积. -
25. 如图,ABC在直角坐标系中,
 (1)、请写出ABC 三个顶点的坐标;(2)、在x轴上找一点P,使PA+PB的值最小,请在图中表示出点P的位置并写出点P的坐标。
(1)、请写出ABC 三个顶点的坐标;(2)、在x轴上找一点P,使PA+PB的值最小,请在图中表示出点P的位置并写出点P的坐标。 -
26. 某农谷生态园响应国家发展有机农业政策,大力种植有机蔬菜,某超市看好甲、乙两种有机蔬菜的市场价值,经调查甲种蔬菜进价每千克m元,售价每千克16元;乙种蔬菜进价每千克n元,售价每千克18元。(1)、该超市购进甲种蔬菜10千克和乙种蔬菜5千克需要170元;购进甲种蔬菜6千克和乙种蔬菜10千克需要200元.求m,n的值。(2)、该超市决定每天购进甲、乙两种蔬菜共100千克,且投入资金不少于1160元又不多于1168元,设购买甲种蔬菜x千克(x为整数),求有哪几种购买方案。(3)、在(2)的条件下,求超市在获得的利润的最大值。
