广西北部湾经济区2021年数学中考全真模拟试卷（五）

试卷更新日期：2021-06-17 类型：中考模拟

进入出卷网下载

一、选择题(共12小题，每小题3分，共36分。在每小题给出的四个选项中只有一项是符合要求的，用2B铅笔把答题卡上对应题目的答案标号涂黑。)

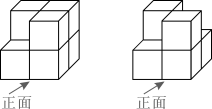
1. -3的倒数是（）

A、3 B、-3 C、 $- \frac{1}{3}$ D、 $\frac{1}{3}$

查看试题解析
2. 2020年6月23日，我国的北斗卫星导航系统（BDS）星座部署完成，其中一颗中高轨道卫星高度大约是21500000米.将数字21500000用科学记数法表示为（）

A、 0.215×10⁸ B、2.15×10⁷ C、2.15×10⁶ D、21.5×10⁶

查看试题解析
3. 如图的两个几何体分别由7个和6个相同的小正方体搭成，比较两个几何体的三视图，正确的是（）

A、仅主视图不同 B、仅俯视图不同 C、仅左视图不同 D、主视图、左视图和俯视图都相同

查看试题解析
4. 下列说法正确的是（）

A、“买中奖率为 $\frac{1}{10}$ 的奖券10张，中奖”是必然事件 B、“汽车累积行驶10000km，从未出现故障”是不可能事件 C、气象局预报说“明天的降水概率为70%”，意味着明天一定下雨 D、抛掷一枚质地均匀的硬币，正面朝上的概率为0.5

查看试题解析
5. 下列计算正确的是（）

A、a²·a²＝2a⁴ B、(－a²)³＝－a⁶ C、3a²－6a²＝3a² D、(a－2)²＝a²－4

查看试题解析
6. 将抛物线y=x²-2x+3向上平移3个单位长度，再向右平移2个单位长度后，得到抛物线的解析式为（）

A、y=(x-1)²+5 B、y=(x-3)²+5 C、y=(x+2)³+6 D、y=(x-4)²+6

查看试题解析
7. 如图，在△ABC中，∠C=60°，AD是BC边上的高，点E为AD的中点，连接BE并延长交AC于点F。若∠AFB=90°，EF=2，则BF长为（）

A、4 B、6 C、8 D、10

查看试题解析
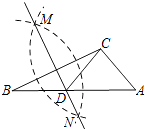
8. 如图，在已知的△ABC中，按以下步骤作图：
①分别以B，C为圆心，以大于 $\frac{1}{2}$ BC的长为半径作弧，两弧相交于两点M，N；
②作直线MN交AB于点D，连接CD．
若CD=AC，∠A=50°，则∠ACB的度数为（）

A、90° B、95° C、100° D、105°

查看试题解析
9. 某工程队几名工人建造绿地，随着技术的提高，公司采用了新的快捷的建造工具，由每周建造3000平方米提高到4200平方米，而且平均每人每周比原来多建造80平方米，若公司的工作人员人数不变，求原来平均每人每周建造多少平方米？设原来平均每人每周建造x平方米，根据题意可列方程为（）

A、 $\frac{3000}{x} = \frac{4200}{x - 80}$ B、 $\frac{3000}{x} + 80 = \frac{4200}{x}$ C、 $\frac{4200}{x} = \frac{3000}{x} - 80$ D、 $\frac{3000}{x} = \frac{4200}{x + 80}$

查看试题解析
10. 《九章算术》是我国古代数学成就的杰出代表，其中《方田》章给出计算弧田面积所用公式为：弧田面积= $\frac{1}{2}$ (弦x矢+矢²)，弧田(如图)是由圆弧和其所对的弦所围成，公式中“弦”指圆弧所对弦长AB，“矢”等于半径长与圆心O到弦的距离之差．在如图所示的弧田中，“弦”为8，“矢”为3，则cos∠OAB=（）

A、 $\frac{3}{5}$ B、 $\frac{24}{25}$ C、 $\frac{4}{5}$ D、 $\frac{12}{25}$

查看试题解析
11. 如图，△OA₁B₁ ， △A₁A₂B₂ ， △A₂A₃B₃ ， ……是分别以B₁ ， B₂ ， B₃ ， ……为直角顶点，斜边在x轴正半轴上的等腰直角三角形，其直角顶点B₁(x₁ ， y₁)，B₂(x₂ ， y₂)，B₃(x₃ ， y₃)，……均在反比例函数y= $\frac{4}{x}$ (x>0)的图象上，则y₁+y₂+……+y₁₀的值为（）

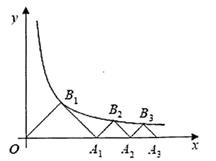A、2 $\sqrt{10}$ B、6 C、4 $\sqrt{2}$ D、2 $\sqrt{7}$

查看试题解析
12. 如图，AC为边长为2 $\sqrt{3}$ 的菱形ABCD的对角线，∠ABC=60°，点M，N分别从点B，C同时出发，以相同的速度沿BC，CA向终点C和A运动，连接AM和BN，求△APB面积的最大值是（）

A、2 $\sqrt{3}$ B、4+2 $\sqrt{3}$ C、1+ $\sqrt{3}$ D、 $\sqrt{3}$

查看试题解析

二、填空题(本小题共6小题，每小题3分，共18分)

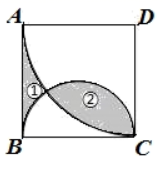
13. 若二次根式 $\sqrt{2021 - x}$ 有意义，则x的取值范围是.

查看试题解析
14. 因式分解：4a³-16a²+16a=

查看试题解析
15. 等腰三角形的两条边长分别为3和4，则这个等腰三角形的周长是．

查看试题解析
16. 端午节是我国传统佳节，小峰同学带了4个粽子(除粽馅不同外，其他均相同)，其中有两个肉馅粽子、一个红枣粽子和一个豆沙粽子，准备从中任意拿出两个送给他的好朋友小悦，小悦拿到的两个粽子都是肉馅的概率是

查看试题解析
17. 如图，在边长为2的正方形ABCD中，以点D为圆心.AD的长为半径画弧，再以BC为直径画半圆.若阴影部分①的面积为S₁ ，阴影部分②的面积为S₂ ，则S₂-S₁的值为.

查看试题解析
18. 如图，在矩形AOBC中，OB=4，OA=3，分别以OB、OA所在直线为x轴和y轴，建立如图所示的平面直角坐标系，F是边BC上的一个动点(不与B、C重合)，过F点的反比例函数y= $\frac{k}{x}$ (k>0)的图象与AC边交于点E，将△CEF沿EF对折后，C点恰好落在OB上的点D处，则k的值可为

查看试题解析

三、解答题(本大题共8小题，共66分。解答应写出文字说明或验算步骤)

19. 计算：|1- $\sqrt{2}$ |-（ $\frac{1}{3}$ ）^-1+（2020-π）⁰-2cos45°

查看试题解析
20. 先化简，再求值： $\frac{a + 1}{a^{2} - 2 a + 1} \div (2 + \frac{3 - a}{a - 1})$ ，其中a=2．

查看试题解析
21. 如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，△ABC的三个顶点A(5，2)、B(5，5)、C(1，1)均在格点上。

( 1 )将△ABC向下平移5个单位得到△A₁B₁C₁ ，并写出点A₁的坐标；

( 2 )画出△A₁B₁C₁绕点C₁逆时针旋转90°后得到的△A₂B₂C₁ ，并写出点A₂的坐标；．

( 3 )在(2)的条件下，求△A₁B₁C₁在旋转过程中扫过的面积(结果保留π)

查看试题解析
22. 电影《你好，李焕英》成为今年春节电影档的黑马，截至2021年3月17日票房已达52.78亿。为了解大家对这部电影的喜爱程度，小李3月17日在百丽宫电影院、西城天街UME电影院观看这部电影的观众中，各抽取了m名观众，统计这部分观众对电影的评价分数(满分10分，用x表示评价分数，共分为4组：A：9<x≤10；B：8<x≤9；C：7<x≤8；D：0≤x≤7)，并对数据进行整理、描述和分析，下面给出了部分信息。

其中百丽宫观众的评分位于A组有14人，评分分别为：

10，10，9.8，9.8，9.7，9.6，9.6，9.5，9.5，9.4，9.2，9.2，9.2，9.2；

两家电影院观众评分的平均数，中位数，众数(单位：分)如表所示：

电影院

百丽宫

UME

平均数

9.2

9.2

中位数

n

9.5

众数

9.2

9.5

(1)、填空：m= ， n= ，并补全条形统计图；

(2)、通过以上数据分析，你认为哪个电影院的观众更欢这部电影？请说明理由(一条理由即可)；

(3)、3月17日，百丽宫电影院、UME电影院共有1000人观看这部电影，请估计这1000人中给出这部电影评分高于9分的观众人数是多少？

查看试题解析
23. 请阅读下列材料，并完成相应的任务．
克罗狄斯·托勒密(约90年- 168 年)，古希腊天文学家、地理学家和光学家，在数学方面，他还论证了四边形的特性，即有名的托勒密定理，托勒密定理的内容如下：

圆的内接四边形的两条对角线的乘积等于两组对边乘积的和，即：如图1，若四边形ABCD

内接于⊙O，则有

任务：

(1)、材料中划横线部分应填写的内容为

(2)、已知，如图2，四边形ABCD内接于⊙O，BD平分∠ABC，∠COD=120%，求证：BD=AB+BC

查看试题解析

24. 某网店销售的消毒用紫外线灯很畅销，该网店店主结合店铺数据发现，日销量y(件)是售价x (元/件)的一次函数，其售价、日销售量、日销售纯利润w (元)的四组对应值如表：

售价x (元/件)	150	160	170	180
日销售量y (件)	200	180	160	140
日销售纯利润w (元)	8000	8800	9200	9200

另外，该网店每日的固定成本折算下来为2000元。

注：日销售纯利润=日销售量×(售价-进价)-每日固定成本

(1)、①求y关于x的函数解析式(不要求写出自变量的取值范围)；

②该商品进价是元/件，当售价是元/件时，日销售纯利润最大，最大纯利润是元。

(2)、每件紫外线灯的进价提高了m元(m>0)，且每日固定成本增加了100元，但该店主为响应政府号召，落实用品限价规定，按售价不高于170元/件销售，若此时的日销售纯利润最高为7500元，求m的值。

查看试题解析

25. 如图，抛物线经过点A(-1，0)，B(3，0)，C(0，3)。过抛物线上一个动点D作x轴的平行线，交抛物线于点E，过点D、E分别作DG⊥x轴于G，EF⊥x轴于F。

(1)、求抛物线的解析式。

(2)、设点D的横坐标为m，四边形DEFG的周长为I，当1<m<3时，求I关于m的函数关系式，并求出当l取最大值时点D的坐标。

(3)、在(2)的条件下，若点P在抛物线上，点Q在抛物线的对称轴上，是否存在以点A、D、P、Q为顶点的四边形为平行四边形？若存在，请写出相应的点P的坐标；若不存在，请说明理由。

查看试题解析
26. 在一次数学研究性学习中，小兵将两个全等的直角三角形纸片ABC和DEF拼在一起，使点A与点F重合，点C与点D重合(如图1)，其中∠ACB=∠DFE=90°，BC=EF=3cm，AC=DF=4cm，并进行如下研究活动。

活动一：将图1中的纸片DEF沿AC方向平移，连接AE，BD(如图2)，当点F与点C重合时停止平移。

[思考]图2中的四边形ABDE是平行四边形吗？请说明理由。

[发现]当纸片DEF平移到某一位置时，小兵发现四边形ABDE为矩形(如图3)。求AF的长。

活动二：在图3中，取AD的中点O，再将纸片DEF绕点O顺时针方向旋转a度(0≤a≤90)，连接OB，OE (如图4)。

[探究]当EF平分∠AEO时，探究OF与BD的数量关系，并说明理由。

查看试题解析

电影院	百丽宫	UME
平均数	9.2	9.2
中位数	n	9.5
众数	9.2	9.5