浙江省金华市婺城区2021年数学中考冲刺卷（二）
试卷更新日期：2021-06-17 类型：中考模拟
一、选择题(本大题有10小题，每小题3分，共30分)
-
1. 如果a与-2021互为相反数，那么a （ ）A、-2021 B、2021 C、 D、2. 2021年5月22日，中国工程院院士袁隆平在长沙不幸逝世。这位“共和国勋章获得者”的最大贡献是杂交水稻技术。2020年我国水稻种植面积4.5亿亩，其中50%左右是杂交水稻，则杂交水稻种植面积用科学记数法表示为 （ ）A、4.5×108亩 B、2.25×108亩 C、4.5×109亩 D、2.25×109亩3. 如图，一个圆柱体被截去一部分，则该几何体的主视图 （ ）
A、
B、
C、
D、
4. 小马虎做题很快，但经常不仔细思考，所以往往错误率很高，有一次做了四个题，但只做对了一个，他做对的是（ ）A、(2x3)2=2x6 B、a2·a3=a6 C、 =±2 D、2x3·x2=2x55. 围棋起源于中国，古代称之为“弈”，至今已有4000多年的历史.2017年5月，世界围棋冠军柯洁与人工智能机器人AlphaGo 进行围棋人机大战．截取首局对战棋谱中的四个部分，由黑白棋子摆成的图案是中心对称（ ）A、
B、
C、
D、
6. 测试五位学生的“一分钟跳绳”成绩，得到五个各不相同的数据，在统计时，出现了一处错误：将最高成绩写得更高了，计算结果不受影响（ )A、方差 B、标准差 C、中位数 D、平均数7. 三个全等三角形按如图的形式摆放，则∠1+∠2+∠3的度数是（ ）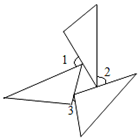
A、90° B、120° C、135° D、180°8. 如图是一张高脚木凳，AC∥EF∥GH，AB=CD，点E，G是AB的三等分点，已知EF与GH之间的距离为25cm，∠EGH=80°，则椅脚AB的长度为 cm（ ）
A、 B、75sin80° C、 D、9. 如图，已知点P1为直线I：y=-2x+6上一点，先将点P向下平移a个单位，再向右平移3个单位至点P2 ， 然后再将点P2向下平移2个单位，向右平移b个单位至点P3。若点P3恰好落在直线l上，则a，b应满足的关系（ ）
A、a-2b=4 B、b-2a=1 C、a+2b=8 D、2a+b=710. 如图，在Rt△ABC中，∠ACB=90°，分别以其三边为边向外作正方形，延长EA交BG于点M，连接IM交AB于点N，若M是BG的中点，则 的值为（ ）
A、 B、 C、 D、二、填空题(本题有6小题，每小题4分，共24分)
-
11. 分解因式：16-4x2=12. 某科幻小说上、下各1册，小明随机将它们叠放在一起，从上到下的顺序恰好为“上册、下册”的概率是13. 商家花费760元购进某种水果80千克，销售中有5%的水果正常损耗．为了避免亏本，售价至少应定为元千克14. 现在很多家庭都使用折叠型西餐桌来节省空间，两边翻开后成圆形桌面(如图1)。餐桌两边AD和BC平行且相等(如图2)，小华用皮带尺量出AC=4米，AB=2米，那么桌面翻成圆桌后，桌子面积会增加平方米。(结果保留π)．
15. 如图，菱形ABCD顶点A在函数y= (x>0)的图象上，函数y= (k>12，x>0)的图象关于直线AC对称，且经过点B，D两点，若AB=4，∠DAB=30°，则k的值为
16. 有一种双层长方体垃圾桶AB=70cm，BC=25cm，CF=30cm，侧面如图1所示，隔板EG等分上下两层，下方内桶BCHG绕底部轴(CF)旋转开，若点H恰好能卡在原来点G的位置，则内桶边CH的长度应设计为；现将CH调整为25cm，打开最大角度时，卡在隔板上，如图2所示，则可完全放入下方内桶的球体的直径不大于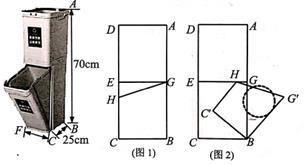
三、解答题(本题有8小题，共66分，每题都必须写出解答过程)
-
17. 计算：3tan30°+| -2|-( )-2+(sin60°-1)018. 解方程：(x-1)(2x+3)=(2x+3)．19. 如图，在4×5的正方形网格中，每个小正方形的边长为1，点AB在格点上，点C是线段AB与格线的交点。利用网格和无刻度的直尺按下列要求画图。
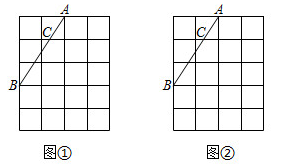(1)、在图①中，过点B作AB的垂线。(2)、在图②中，过点C作AB的垂线。20. 今年的7月1日是中国共产党成立100周年纪念日，我市某中学开展了爱党宣传教育活动.为了了解这次宣传活动的效果，学校从全校1200名学生中随机抽取了部分学生进行知识测试，并将测试成绩分为 五个等级，绘制成了如下统计图（部分信息未给出）.
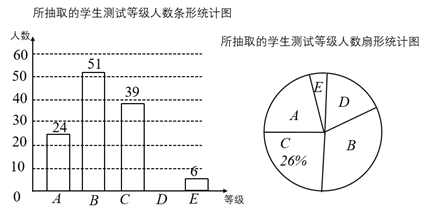(1)、求本次被调查的学生人数，并补全条形统计图.(2)、求扇形统计图中“A”所对应的扇形圆心角的度数.(3)、如果测试成绩为 等级的均为优秀，请估计该校学生中成绩为优秀的人数.21. 如图1是一种手机平板支架，由底座、支撑板和托板构成，手机放置在托板上，如图2是其侧面示意图，量得底座长AB=11cm，支撑板长BC=8cm，托板长CD=6cm，托板CD固定在支撑板顶端点C处，托板CD可绕点C旋转，支撑板BC可绕点B转动。
(1)、如果∠ABC=60°，∠BCD=70，求点D到直线AB的距离(精确到0.1cm)；(2)、在第(1)小题的条件下，如果把线段CD绕点C顺时针旋转20°后， 再将线段BC绕点B逆时针旋转，使点D落在直线AB上，求线段BC旋转的角度．(参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，sin37°≈0.60，cos37°≈0.80，tan37°≈0.75， ≈1.73)
22. 如图，四边形ABCD是平行四边形，以AB为直径的⊙O与CD边相切于点E，BC交⊙O于点F(AF>BF)，连接AE，EF。
(1)、求证：△FCE∽△FEA；(2)、若⊙O的半径是 ，且 ，求AD的长．23. 如图，在平面直角坐标系xOy中，抛物线y=ax2+bx+c(a>0)与x轴相交于A(-1，0)，B(3，0)两点，点C为抛物线的顶点。点M(0，m)为y轴上的动点，将抛物线绕点M旋转180°，得到新的抛物线，其中B、C旋转后的对应点分别记为B'、C'
(1)、若原抛物线经过点(-2，5)，求原抛物线的函数表达式；(2)、在(1)的条件下，当四边形BCB'C的面积为40时，求m的值；(3)、探究a满足什么条件时，存在点M，使得四边形BCB'C'为菱形？请说明理由。24. 已知，在矩形ABCD中，AB=4， AD=6，点E是边AD上的一个点(与点A、D不重合)，联结CE，作∠CEF=90°交直线BC于点F。点G为线段EP的中点。
(1)、如图1，联结BG，若点E是AD的中点，求△BFG的面积； ．(2)、如图2，若将边AD向左平移1个单位得 A'BCD'，当点G落在边A'B上时，求A'E的长；(3)、如图3，连接DF，点H是DF的中点，连接GH，EH，是否存在点E，使△EGH为等腰三角形？若存在，画出图形并求出DE2的值。