浙江省宁波市余姚市2020-2021学年阳明杯竞赛八年级下学期数学试卷

试卷更新日期：2021-06-17 类型：竞赛测试

进入出卷网下载

一、选择题（共8小题，每题4分）

1. 下列二次根式是最简二次根式的是（）

A、 $\sqrt{12}$ B、 $\sqrt{2.4}$ C、 $\sqrt{3}$ D、 $\sqrt{\frac{1}{3}}$

查看试题解析
2. 若关于x的一元二次方程 $x^{2} + 3 x + k - 2 = 0$ 有两个不相等的实数根，则实数k的取值范围是（）

A、k＞ $\frac{17}{4}$ B、k≥ $\frac{17}{4}$ C、k＜ $\frac{17}{4}$ D、k≤ $\frac{17}{4}$

查看试题解析
3. 如图，在直角三角形ABC中，∠C＝90°，AB＝10，AC＝8，点E、F分别为AC和AB的中点，则EF＝（）

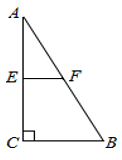A、3 B、4 C、5 D、6

查看试题解析
4. 如图，平行四边形ABCD的对角线交于点E ，已知AB＝5cm ， △ABE的周长比△BEC的周长小3cm ，则AD的长度为（）

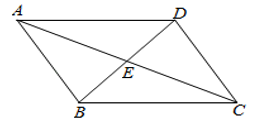A、8cm B、5cm C、3cm D、2cm

查看试题解析
5. 菱形具有而矩形不具有的性质是（）

A、对角线互相平分 B、对角线相等 C、对角相等 D、对角线互相垂直

查看试题解析
6. 已知，有下列各数： $2 ， 3 ， 3 ， 5 ， 5 ， 6 ， 7 ， x$ 组成的数据，其中这组数据的众数是 $3$ ，则该组数据的中位数为（）

A、5 B、4 C、3 D、2

查看试题解析
7. 用反证法证明“在三角形中，至少有一个内角大于或等于60°”时，应先假设（）

A、在三角形中，三个内角都大于60° B、在三角形中，三个内角都小于60° C、在三角形中，至少有一个内角大于60° D、在三角形中，至少有一个内角小于60°

查看试题解析
8. 如图，矩形ABCD和矩形CEFG，AB＝1，BC＝CG＝2，CE＝4，点P在边GF上，点Q在边CE上，且PF＝CQ，连结AC和PQ，N，M分别是AC，PQ的中点，则MN的长为（）

A、3 B、6 C、 $\frac{\sqrt{37}}{2}$ D、 $\frac{\sqrt{17}}{2}$

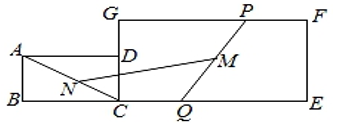查看试题解析

二、填空题（共6小题，每题5分）

9. 比较大小： $- 3 \sqrt{2}$ $- 2 \sqrt{3}$

查看试题解析
10. 已知样本数据为3，4，2，1，5，则标准差是。

查看试题解析
11. 一个多边形的内角和是720°，这个多边形的边数是．

查看试题解析
12. 已知x＝1是关于x的方程x²+mx+3＝0的一个根，则方程的另一个根是．

查看试题解析
13. 如图，已知一次函数 $y_{1} = 3 x$ 的图象与反比例函数 $y_{2} = \frac{k}{x}$ 的图象交于点A（a ， 3）．则当 $x$ 的取值范围满足时， $y_{1} > y_{2}$ .

查看试题解析
14. 如图，在菱形ABCD中．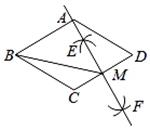

（ 1 ）分别以C ， D为圆心，大于 $\frac{1}{2}$ CD长为半径作弧，两弧分别交于点E ， F；

（ 2 ）作直线EF交边CD于点M ，且直线EF恰好经过点A

（ 3 ）连接BM ．

根据以上作图过程及所作图形，判断下列结论中正确的有．（填序号）

①∠ABC＝60° ②BC＝2CM

③S_△_ABM＝2S_△_ADM④如果AB＝2，那么BM＝4

查看试题解析

三、解答题（共7小题）

15.

(1)、计算： $\frac{1}{2} \sqrt{20} - \sqrt{5} + 3 \sqrt{\frac{1}{5}}$

(2)、解方程： ${(x - 1)}^{2} = 2 x + 1$

查看试题解析
16. 图1，图2，图3均是由边长为1的正三角形构成的网格，每个网格图中有5个正三角形已涂上阴影.请在余下的空白正三角形中，按下列要求涂上阴影：

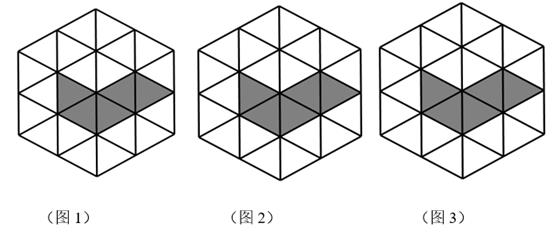(1)、在图1中涂上一个阴影正三角形，使得阴影部分图形是中心对称图形，但不是轴对称图形.

(2)、在图2中涂上两个阴影正三角形，使得阴影部分图形是轴对称图形，但不是中心对称图形.

(3)、在图3中涂上三个阴影正三角形，使得阴影部分图形既是中心对称图形，又是轴对称图形.

查看试题解析

17. 我区某校德育处积极开展“预防新冠病毒知识知多少”宣传活动，组织举办了一次防病毒知识竞赛，本次竞赛满分10分，学生得分均为整数，成绩达到6分及6分以上为合格，达到9分或10分为优秀，在这次竞赛中，甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图所示．

组别	平均分	中位数	方差	合格率	优秀率
甲组	6.8	a	3.76	90%	30%
乙组	b	7.5	1.96	80%	20%

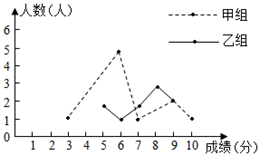
解答下列问题：

(1)、填空：a＝；b＝．

(2)、小敏说：“这次竞赛我得了7分，在我们小组中排名属中游略偏上．”观察上面表格后思考判断，小敏属于（填“甲”或“乙”）组的学生．

(3)、甲组同学说他们组的合格率、优秀率均高于乙组，所以他们组的成绩比乙组好．但乙组同学不同意甲组同学的说法，认为他们的成绩要好于甲组.请你写出两条支持乙组同学观点的理由．

查看试题解析

18. 如图，在平行四边形ABCD中，E ， F为AB边上的两点，且AE＝BF ， DF＝CE ．

求证：

(1)、平行四边形ABCD是矩形．

(2)、△ADF≌△BCE ．

查看试题解析
19. 随着全球疫情的爆发，医疗物资需求猛增，某企业及时引进一条口罩生产线生产口罩，开工第一天生产口罩5000盒，第三天生产口罩7200盒，若每天增长的百分率相同．

(1)、求每天增长的百分率.

(2)、经调查发现，1条生产线的最大产能是15000盒/天，但是每增加1条生产线，每条生产线的产能将减少500盒/天，现该厂要保证每天生产口罩65000盒，在增加产能的同时又要节省投入的条件下（生产线越多，投入越大），应该增加几条生产线？

查看试题解析
20. 如图，已知矩形OABC中，OA＝3 ， AB＝4 ，反比例函数y＝ $\frac{k}{x}$ （k＞0）的图像与矩形两边AB、BC分别交于点D、E ，且BD＝2AD﹒

(1)、求反比例函数的表达式及点E的坐标；

(2)、若矩形OABC的对角线OB与反比例函数图象相交于点P ，连结PC ，求△POC的面积

查看试题解析

四、附加题试题（共5小题，满分30分）

21. 已知关于x的方程 $a {(x + m)}^{2} + b = 0 (a 、 b 、 m 为常数， a \neq 0)$ 的解是 $x_{1} = 2 ， x_{2} = - 1 ，$ 那么方程 $a {(x + m + 2)}^{2} + b = 0$ 的解是（）

A、 $x_{1} = 2 ， x_{2} = - 1$ B、 $x_{1} = - 2 ， x_{2} = 1$ C、 $x_{1} = 0 ， x_{2} = - 3$ D、条件不足，无法求解

查看试题解析
22. 如图，正方形ABCD由8个全等的直角三角形和小正方形PQMN组成，记正方形ABCD、正方形EFGH、正方形PQMN的面积为x 、y、z.若EF的长为 $\sqrt{6}$ ，则 x+y+z=（）

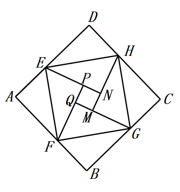A、12 B、18 C、 $2 \sqrt{6}$ D、 $4 \sqrt{6}$

查看试题解析
23. 如图，将矩形ABCD沿EF折叠，使点D落在点B处，点C落在点C'处，P为折痕EF上的任意一点，过点P作PG⊥BE ， PH⊥BC ，垂足分别为G ， H ，若AD＝16，CF＝6，则PG+PH＝．

查看试题解析
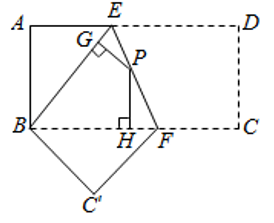24. 如图，12个边长为1的正方形摆放在平面直角坐标系中，过点A（-1，0）的直线AB将这12个正方形面积相等的两部分，且直线与反比例函数y＝ $\frac{k}{x}$ （k<0）的图象交于点C ，与y轴交于点B ，若△AOB与△BOC的面积之比为1：3，则k的值为．

查看试题解析
25. 如图，在矩形ABCD中，AB=6 ， BC=8 ，将矩形ABCD绕点D按顺时针方向旋转，得到矩形EFGD ，直线DE ， FG分别与直线BC交于点P ， Q.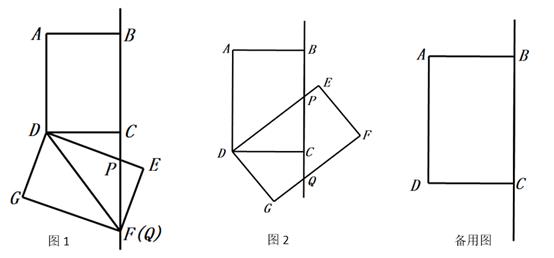

(1)、如图1，当矩形EFGD的顶点F落在线段BC的延长线上时，求DP的长．

(2)、如图2，在矩形旋转过程中，当P位于线段BC上时，求证：DP=PQ.

(3)、在旋转过程中，旋转角 $α$ 满足 $0^{\circ} < α \leq 90^{\circ}$ ，当 $B P = \frac{1}{2} B Q$ 时，求CP的长（直接写出答案）.

查看试题解析