浙江省宁波市余姚市2020-2021学年阳明杯竞赛七年级下学期数学试卷

试卷更新日期：2021-06-17 类型：竞赛测试

进入出卷网下载

一、选择题（每小题4分，共32分。）

1. 下列是二元一次方程的是（）

A、 $x + 2 y$ B、 $\frac{1}{x} + y = 0$ C、x=y²+1 D、x+y=1

查看试题解析
2. 下列计算结果正确的是（）

A、 $a^{3} \times a^{4} = a^{12}$ B、 ${(a^{3})}^{2} = a^{6}$ C、 ${(a b^{2})}^{3} = a b^{6}$ D、 $a^{5} \div a = a^{5}$

查看试题解析
3. 下列调查中，需要采用全面调查方式的是（）

A、对某批次汽车的抗撞击能力的调查 B、为防控新冠肺炎，对高风险地区人员进行核酸检测 C、对全国中学生课外阅读情况的调查 D、对某一批次盒装牛奶的合格情况的调查

查看试题解析
4. 如图，能判定DE∥BC的条件是（）

A、∠ABC+∠BAE=180 B、∠C=∠BAC C、∠C+∠BAD=180 D、∠C=∠BAD

查看试题解析
5. 下列分解因式正确的是（）

A、a²－4=（a－2）² B、 $- x y^{2} + 2 x y - y = - y (x y - 2 x)$ C、 $2 x^{2} - 8 x + 8 = 2 {(x - 2)}^{2}$ D、 $x^{2} + 2 x y - y^{2} = {(x - y)}^{2}$

查看试题解析
6. 如图，在框中解分式方程的4个步骤中，根据等式基本性质的是（）

A、①③ B、②④ C、①② D、③④

查看试题解析
7. 对于分式 $\frac{x + a}{3 x - 1}$ ，当 $x = - a$ 时，下列结论正确的是（）

A、分式无意义 B、分式值为0 C、当 $a \neq - \frac{1}{3}$ 时，分式的值为0 D、当 $a \neq \frac{1}{3}$ 时，分式的值为0

查看试题解析
8. 已知 $4 x^{2} + 1$ 加上一个单项式后能成为一个整式的完全平方，给出下面四个单项式① $4 x$ ， ② $- 2 x$ ， ③ $-$ 1 ， ④ $4 x^{4}$ ，其中满足条件的共有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题（每小题5分，共30分）

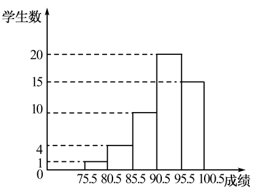
9. 石墨烯是目前世界上最薄、最坚硬的纳米材料，厚度仅0.000 0034m，用科学记数法表示0.000 0034= ．

查看试题解析
10. 已知a﹣b＝3，ab＝﹣2，则a²b﹣ab²的值为．

查看试题解析
11. 若多项式x²+m x+n可以因式分解为 $(x - 2) (x + 3)$ ，则 $m - n$ 的值为．

查看试题解析
12. 七年级（1）班一次数学单元测试，全班所有学生成绩的频数直方图如图所示（满分100分，成绩取整数），则成绩在90.5～95.5这一分数段的频率是．

查看试题解析
13. 将一把直尺和一块直角三角板如图放置，如果∠α=43°，则∠β的度数是度．

查看试题解析
14. 在“幻方拓展课程”探索中，小明在如图的3×3方格内填入了一些表示数的代数式，若图中各行、各列及对角线上的三个数之和都相等，则 ${(2 y)}^{x}$ 的值为．

查看试题解析

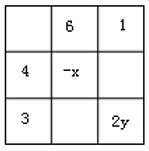
三、解答题（共58分）

15. 计算下列各题

(1)、 $x^{2} \cdot x^{3} + x^{7} \div x^{2}$

(2)、 ${(x - 2)}^{2} - {(x + 1)}^{} (x - 1)$

(3)、 $\frac{2}{a^{2} - 1} + \frac{1}{a + 1}$

查看试题解析
16. 解方程（组）

(1)、 ${\begin{cases} 2 x - y = 5 \\ 3 x + 2 y = 4 \end{cases}$

(2)、 $\frac{2 - x}{x - 3} = \frac{1}{3 - x} - 2$

查看试题解析
17. 如图，已知∠1=∠2，∠B=∠C ，可推得AB∥CD ．理由如下：
∵∠1=∠2（已知），

又∠1=∠CGD（        ）

∴∠2=∠CGD

∴CE∥BF（        ）

∴∠_▲_=∠BFD（        ）

又∵∠B=∠C（已知）

∴__▲__

∴AB∥CD（        ）

查看试题解析
18. 如图，正方形网格中有一个△ABC（其中A，B，C均在格点上），按要求进行下列作图（只借助于网格，需标上字母写出结论）

（ 1 ）过点A画出BC的平行线；

（ 2 ）画出先将△ABC向右平移5格，再向上平移3格后的△DEF；

查看试题解析
19. 为提高学生的音乐素养，培养学生的音乐兴趣，某校举行了一次“听音辨曲”活动．随机抽取了部分学生进行测试，并将测试成绩从高到低分为A（优秀），B（良好），C（合格），D（不合格）四个等级，制作了如下的统计图（扇形统计图中，等级“C”所对应的扇形的圆心角为90度，部分信息不完整）：

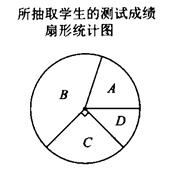
根据上述统计图，完成以下问题：

(1)、这次共抽取了名学生；在扇形统计图中，等级“D”所对应的扇形的圆心角是度．

(2)、请把条形统计图补充完整．

(3)、已知该校共有1800名学生参加测试，请你估算该校获得等级“A”的学生人数．

查看试题解析
20. 材料阅读：若一个整数能表示成a²+b²（a、b是正整数）的形式，则称这个数为“完美数”．例如：因为13=3²+2² ，所以13是“完美数”；再如：因为a²+2ab+2b²=（a+b）²+b²（a、b是正整数），所以a²+2ab+2b²也是“完美数”．

(1)、解决问题：
请你写出一个大于20小于30 的“完美数”，并判断53是否为“完美数”；

(2)、探究问题：
①已知x²+y²-2x+4y+5＝0，求x+y的值．

②已知S＝x²+4y²+4x-12y+k（x、y是整数，k是常数），要使S为“完美数”，试求出符合条件的一个k值，并说明理由．

查看试题解析

四、附加选择题（每小题4分，共8分）

21. 已知 $M = a^{2} + 4 b^{2} ， N = 4 a b$ （ $a ， b$ 为任意有理数），则M与N的大小关系是（）

A、M>N B、M<N C、M ≥N D、M ≤ N

查看试题解析
22. 如图，大长方形ABCD是由一张周长为C₁正方形纸片①和四张周长分别为C₂ ， C₃ ， C₄ ， C₅的长方形纸片②，③，④，⑤拼成，若大长方形周长为定值，则下列各式中为定值的是（）

A、C₁ B、C₃+C₅ C、C₁+C₃+C₅ D、C₁+C₂+C₄

查看试题解析

五、附加填空题（每小题5分，共10分）

23. 如果关于x的分式方程 $\frac{4}{x - 3} = 1 + \frac{m}{x - 3}$ 有增根，则m的值为．

查看试题解析
24. a ， b是实数，定义关于“*”的一种运算：a*b＝ $（ a + b)^{2} - {(a - b)}^{2}$ ．则下列结论：
①a*b＝0，则a＝0或b＝0； ②不存在实数a ， b ，满足a*b＝4a²+b²；

③a*（b+c）＝a*b+a*c； ④a*b＝8，则（10ab³）÷（5b²）＝4 ，

其中正确的结论是．（用序号表示出所有正确的结论）

查看试题解析

六、附加解答题

25. 一张如图1的长方形铁皮，四个角都剪去边长为 30 厘米的正方形，再四周折起，做成一个有底无盖的铁盒如图2．

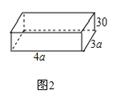(1)、现有一批图1规格的铁皮需甲、乙两队加工，已知甲队加工300张铁皮与乙队加工360张铁皮所用时间相同. 若乙队每天比甲队多加工30张，求甲队每天加工铁皮的张数.

(2)、已知铁盒底面长方形的长是 $4 a$ cm，宽是 $3 a$ cm，这个无盖铁盒各个面的面积之和称为铁盒的全面积．
①若要在铁盒的各个外表面漆上某种油漆，每元钱可漆的面积为 $\frac{a}{50}$ （cm²），则油漆这个铁盒需要多少钱（用含 $a$ 的代数式表示）？

②是否存在一个正整数 $a$ ，使得铁盒的全面积是底面积的正整数倍？若存在，请求出所有 $a$ ，若不存在，请说明理由．

查看试题解析