山东省烟台市龙口市西片2020-2021学年八年级下学期数学期中试卷（五四学制）

试卷更新日期：2021-06-17 类型：期中考试

进入出卷网下载

一、选择题（共12小题）

1. 二次根式 $\sqrt{\frac{1}{2}}$ 、 $\sqrt{12}$ 、 $\sqrt{30}$ 、 $\sqrt{x + 2}$ 、 $\sqrt{40 x^{2}}$ 、 $\sqrt{x^{2} + y^{2}}$ 中，最简二次根式有（）

A、1 个 B、2 个 C、3 个 D、4个

查看试题解析

2. 观察下列表格，一元二次方程x²﹣x＝1.1的一个解x所在的范围是（）

x	1.1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9
x²﹣x	0.11	0.24	0.39	0.56	0.75	0.96	1.19	1.44	1.71

A、1.5＜x＜1.6 B、1.6＜x＜1.7 C、1.7＜x＜1.8 D、1.8＜x＜1.9

查看试题解析

3. 已知三角形的两边长为4和5，第三边的长是方程x²﹣5x+6＝0的一个根，则这个三角形的周长是（）

A、11 B、12 C、11或12 D、15

查看试题解析
4. 若关于x的一元二次方程nx²﹣2x﹣1=0无实数根，则一次函数y=（n+1）x﹣n的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 若式子 $\frac{\sqrt{a + 2}}{a - 1}$ 有意义，则实数a的取值范围是（　　）

A、a≥﹣2 B、a≠1 C、a＞1 D、a≥﹣2且a≠1

查看试题解析
6. 给出以下方程的解题过程，其中正确的有（）
①解方程 $\frac{1}{2}$ （x﹣2）²＝16，两边同时开方得x﹣2＝±4，移项得x₁＝6，x₂＝﹣2；②解方程x（x﹣ $\frac{1}{2}$ ）＝（x﹣ $\frac{1}{2}$ ），两边同时除以（x﹣ $\frac{1}{2}$ ）得x＝1，所以原方程的根为x₁＝x₂＝1；③解方程（x﹣2）（x﹣1）＝5，由题得x﹣2＝1，x﹣1＝5，解得x₁＝3，x₂＝6；④方程（x﹣m）²＝n的解是x₁＝m+ $\sqrt{n}$ ，x₂＝m﹣ $\sqrt{n}$ ．

A、0个 B、2个 C、3个 D、4个

查看试题解析
7. 若m是方程x²﹣2019x﹣1＝0的根，则（m²﹣2019m+3）•（m²﹣2019m+4）的值为（）

A、16 B、12 C、20 D、30

查看试题解析
8. 用直尺和圆规作一个以线段AB为边的菱形，作图痕迹如图所示，能得到四边形ABCD是菱形的依据是（　　）

A、一组邻边相等的四边形是菱形 B、四边相等的四边形是菱形 C、对角线互相垂直的平行四边形是菱形 D、每条对角线平分一组对角的平行四边形是菱形

查看试题解析
9. 把a $\sqrt{- \frac{1}{a}}$ 根号外的因式移入根号内，运算结果是（）

A、 $\sqrt{a}$ B、 $\sqrt{- a}$ C、﹣ $\sqrt{a}$ D、﹣ $\sqrt{- a}$

查看试题解析
10. 若二次根式 $\sqrt{2 - m}$ 有意义，且关于x的分式方程 $\frac{m}{1 - x}$ +2＝ $\frac{3}{x - 1}$ 有正数解，则符合条件的整数m的和是（）

A、﹣7 B、﹣6 C、﹣5 D、﹣4

查看试题解析
11. 如图，在Rt△ABC中，∠BAC＝90°且AB＝3，AC＝4，点D是斜边BC上的一个动点，过点D分别作DM⊥AB于点M，DN⊥AC于点N，连接MN，则线段MN的最小值为（）

A、 $\frac{12}{5}$ B、 $\frac{5}{2}$ C、3 D、4

查看试题解析
12. 如图，∠BOD＝45°，BO＝DO，点A在OB上，四边形ABCD是矩形，连接AC、BD交于点E，连接OE交AD于点F．下列4个判断：①OE平分∠BOD；②OF＝BD；③DF＝ $\sqrt{2}$ AF；④若点G是线段OF的中点，则△AEG为等腰直角三角形．正确判断的个数是（）

A、4 B、3 C、2 D、1

查看试题解析

二、填空题（共6小题）

13. 若关于x的一元二次方程（m+2）x^|m|+2x﹣1＝0是一元二次方程，则m＝．

查看试题解析
14. 若关于x的一元二次方程kx²+2（k+1）x+k﹣1=0有两个实数根，则k的取值范围是．

查看试题解析
15. 已知实数a满足|2011﹣a|+ $\sqrt{a - 2012} = \sqrt[3]{a^{3}}$ ，求a﹣2011²的值为．

查看试题解析
16.
如图，已知菱形ABCD的周长为16，面积为8 $\sqrt{3}$ ，E为AB的中点，若P为对角线BD上一动点，则EP+AP的最小值为．

查看试题解析
17. 如图，AC是菱形ABCD的对角线，P是AC上的一个动点，过点P分别作AB和BC的垂线，垂足分别是点F和E，若菱形的周长是12cm，面积是6cm² ，则PE+PF的值是cm．

查看试题解析
18. 如图，正方形ABCD的边长为8，点E是BC上的一点，连接AE并延长交射线DC于点F，将△ABE沿直线AE翻折，点B落在点N处，AN的延长线交DC于点M，当AB＝2CF时，则NM的长为．

查看试题解析

三、解答题（共7小题）

19. 计算：

(1)、（ $\sqrt{3}$ ﹣2）²⁰¹⁸（ $\sqrt{3}$ +2）²⁰¹⁹﹣ $\frac{\sqrt{12}}{2}$ ；

(2)、（ $\sqrt{27}$ ×3 $\sqrt{6}$ + $\frac{4}{5} \sqrt{50}$ ﹣8 $\sqrt{\frac{1}{2}}$ ）÷ $\sqrt{2}$

查看试题解析
20. 按要求解下列方程：

(1)、（2x﹣3）²+x（2x﹣3）＝0（因式分解法）；

(2)、2x²﹣4x﹣1＝0（用配方法）．

查看试题解析
21. 已知关于x的二次方程mx²﹣2x+2﹣m＝0．

(1)、证明：不论m为何值时，方程总有实数根；

(2)、当m为何整数时，方程有两个不相等的非负整数根．

查看试题解析
22. 如图，已知△ABC中，AB＝AC，AD是角平分线，F为BA延长线上的一点，AE平分∠FAC，DE∥BA交AE于E．求证：四边形ADCE是矩形．

查看试题解析
23. 阅读下列解题过程
例：若代数式 $\sqrt{{(a - 1)}^{2}} + \sqrt{{(a - 3)}^{2}}$ 的值是2，求a的取值范围．

解：原式＝|a﹣1|+|a﹣3|，

当a＜1时，原式＝（1﹣a）+（3﹣a）＝4﹣2a＝2，解得a＝1（舍去）；

当1≤a≤3时，原式＝（a﹣1）+（3﹣a）＝2＝2，符合条件；

当a＞3时，原式＝（a﹣1）+（a﹣3）＝2a﹣4＝2，解得a＝3（舍去）

所以，a的取值范围是1≤a≤3

上述解题过程主要运用了分类讨论的方法，请你根据上述理解，解答下列问题

(1)、当2≤a≤5时，化简： $\sqrt{{(a - 2)}^{2}} + \sqrt{{(a - 5)}^{2}}$ ＝ 3 ；

(2)、若等式 $\sqrt{{(3 - a)}^{2}} + \sqrt{{(a - 7)}^{2}}$ ＝4成立，则a的取值范围是 3≤a≤7 ；

(3)、若 $\sqrt{{(a + 1)}^{2}} + \sqrt{{(a - 5)}^{2}}$ ＝8，求a的取值．

查看试题解析
24. 如图，四边形ABCD为菱形，P为对角线BD上一点，连接AP并延长交射线BC于点E，连接PC．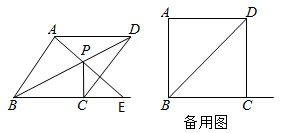

(1)、求证：∠AEB＝∠PCD；

(2)、当PA＝PD且PC⊥BE时，求∠ABC的度数；

(3)、若∠ABC＝90°，△PCE是等腰三角形．直接写出∠PEC的度数．

查看试题解析
25. 已知四边形ABCD是正方形，等腰直角△AEF的直角顶点E在直线BC上（不与点B，C重合），FM⊥AD，交射线AD于点M．

(1)、当点E在边BC上，点M在边AD的延长线上时，如图①，求证：AB+BE＝AM；
（提示：延长MF，交边BC的延长线于点H．）

(2)、当点E在边CB的延长线上，点M在边AD上时，如图②；当点E在边BC的延长线上，点M在边AD上时，如图③．请分别写出线段AB，BE，AM之间的数量关系，不需要证明；

(3)、在（1），（2）的条件下，若BE＝ $\sqrt{3}$ ，∠AFM＝15°，则AM＝．

查看试题解析