广东省深圳市罗湖区2020-2021学年八年级下学期数学期中试卷
试卷更新日期:2021-06-17 类型:期中考试
一、选择题(每小题3分,共30分)
-
1. 下列图形中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. x的 与x的和不超过5用不等式可以表示为( )A、 +x≤5 B、 +x<5 C、 +x≥5 D、 +x>53. 不等式组 的解集在数轴上可表示为( )A、
2. x的 与x的和不超过5用不等式可以表示为( )A、 +x≤5 B、 +x<5 C、 +x≥5 D、 +x>53. 不等式组 的解集在数轴上可表示为( )A、 B、
B、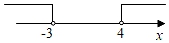 C、
C、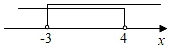 D、
D、 4. 用反证法证明命题“三角形中必有一个内角小于或等于60°”时,首先应假设这个三角形中( )A、有一个内角大于60° B、有一个内角小于60° C、每一个内角都大于60° D、每一个内角都小于60°5. 如图,在△ABC中,AC的垂直平分线交AB于点D,CD平分∠ACB,若∠A=50°,则∠B的度数为( )
4. 用反证法证明命题“三角形中必有一个内角小于或等于60°”时,首先应假设这个三角形中( )A、有一个内角大于60° B、有一个内角小于60° C、每一个内角都大于60° D、每一个内角都小于60°5. 如图,在△ABC中,AC的垂直平分线交AB于点D,CD平分∠ACB,若∠A=50°,则∠B的度数为( )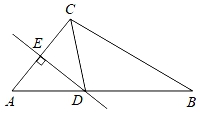 A、25° B、30° C、35° D、40°6. 如图,△ABC中,AB=AC=10cm,BC=8cm,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,并且DE∥AB,则△CDE的周长为( )
A、25° B、30° C、35° D、40°6. 如图,△ABC中,AB=AC=10cm,BC=8cm,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,并且DE∥AB,则△CDE的周长为( )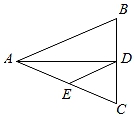 A、20cm B、12cm C、13cm D、14cm7. 如图△ABC中,AB=AC,∠BAC=120°,BC=2 ,D为BC的中点,DE⊥AB,则△EBD的面积为( )
A、20cm B、12cm C、13cm D、14cm7. 如图△ABC中,AB=AC,∠BAC=120°,BC=2 ,D为BC的中点,DE⊥AB,则△EBD的面积为( )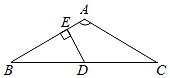 A、 B、 C、 D、8. 不等式组 的非负整数解有( )A、4个 B、5个 C、6个 D、7个9. 如图,是甲、乙两家商店销售同一种产品的销售价y(元)与销售量x(件)之间的函数图象.下列说法:①售2件时甲、乙两家售价一样;②买1件时买乙家的合算;③买3件时买甲家的合算;④买乙家的1件售价约为3元,其中正确的说法是( )
A、 B、 C、 D、8. 不等式组 的非负整数解有( )A、4个 B、5个 C、6个 D、7个9. 如图,是甲、乙两家商店销售同一种产品的销售价y(元)与销售量x(件)之间的函数图象.下列说法:①售2件时甲、乙两家售价一样;②买1件时买乙家的合算;③买3件时买甲家的合算;④买乙家的1件售价约为3元,其中正确的说法是( )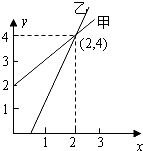 A、①② B、②③④ C、②③ D、①②③10. 如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于( )
A、①② B、②③④ C、②③ D、①②③10. 如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于( )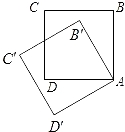 A、1﹣ B、1﹣ C、 D、
A、1﹣ B、1﹣ C、 D、二、填空题(每题3分,共15分)
-
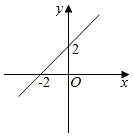
11. 不等式组 解集是 .12. 如图,当y<0时,自变量x的取值范围是 .
 13. 如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于 cm.
13. 如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于 cm.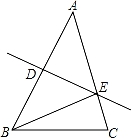 14. 用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素C含量及购买这两种原料的价格如下表:
14. 用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素C含量及购买这两种原料的价格如下表:甲种原料
乙种原料
维生素C含量(单位/千克)
600
100
原料价格(元/千克)
8
4
现配制这种饮料10千克,要求至少含有4200单位的维生素C,若所需甲种原料的质量为x千克,则x应满足的不等式为 .
15. 若等腰三角形一腰上的高等于腰长的一半,则此等腰三角形的二个底角的度数等于 度.三、解答题。(第16题5分,第17题6分,第18题8分,第19题8分,第20题8分,第21题10分,第22题10分,共55分)
-
16. 解不等式5(x﹣1)<6x+1.17. 求不等式组 的解集,并把它的解集表示在数轴上.18. △ABC在平面直角坐标系xOy中的位置如图所示,小正方形的边长为1个单位.
 (1)、作△ABC关于点C成中心对称的△A1B1C1 .(2)、将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2 .(3)、在x轴上求作一点P,使PA1+PC2的值最小,求经过点P和点C2的一次函数关系式,并求出点P的坐标.19. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D在AB边上,斜边DE交AC边于点F.
(1)、作△ABC关于点C成中心对称的△A1B1C1 .(2)、将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2 .(3)、在x轴上求作一点P,使PA1+PC2的值最小,求经过点P和点C2的一次函数关系式,并求出点P的坐标.19. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D在AB边上,斜边DE交AC边于点F. (1)、求n的度数;(2)、求△CDF的面积.20. 某商场计划从厂家购进甲、乙两种不同型号的电视机,已知进价分别为:甲种每台1500元,乙种每台2100元.(1)、若商场购进这两种不同型号的电视机共50台,金额不超过76000元,商场有几种进货方案,并写出具体的进货方案.(2)、在(1)的条件下,若商场销售一台甲、乙型号的电视机的销售价分别为1650元、2300元,以上进货方案中,哪种进货方案获利最多?最多为多少元?21. 已知,如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q.
(1)、求n的度数;(2)、求△CDF的面积.20. 某商场计划从厂家购进甲、乙两种不同型号的电视机,已知进价分别为:甲种每台1500元,乙种每台2100元.(1)、若商场购进这两种不同型号的电视机共50台,金额不超过76000元,商场有几种进货方案,并写出具体的进货方案.(2)、在(1)的条件下,若商场销售一台甲、乙型号的电视机的销售价分别为1650元、2300元,以上进货方案中,哪种进货方案获利最多?最多为多少元?21. 已知,如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q.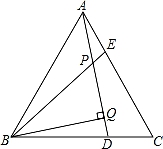 (1)、求证:BE=AD;(2)、求∠BPQ的度数;(3)、若PQ=3,PE=1,求AD的长.22. 已知△AOB和△MON都是等腰直角三角形,∠AOB=∠MON=90°.
(1)、求证:BE=AD;(2)、求∠BPQ的度数;(3)、若PQ=3,PE=1,求AD的长.22. 已知△AOB和△MON都是等腰直角三角形,∠AOB=∠MON=90°.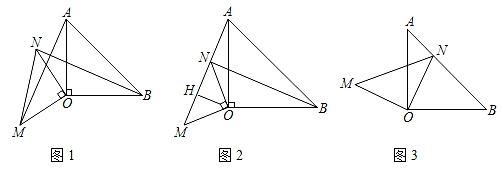 (1)、如图1:连AM,BN,求证:△AOM≌△BON;(2)、若将Rt△MON绕点O顺时针旋转,当点A,M,N恰好在同一条直线上时,如图2所示,线段OH∥BN,OH与AM交点为H,若OB=4,ON=3,求出线段AM的长;(3)、若将△MON绕点O顺时针旋转,当点N恰好落在AB边上时,如图3所示,MN与AO交点为P,求证:MP2+PN2=2PO2 .
(1)、如图1:连AM,BN,求证:△AOM≌△BON;(2)、若将Rt△MON绕点O顺时针旋转,当点A,M,N恰好在同一条直线上时,如图2所示,线段OH∥BN,OH与AM交点为H,若OB=4,ON=3,求出线段AM的长;(3)、若将△MON绕点O顺时针旋转,当点N恰好落在AB边上时,如图3所示,MN与AO交点为P,求证:MP2+PN2=2PO2 .