广东省广州市海珠区2020-2021学年八年级下学期数学期中试卷

试卷更新日期：2021-06-17 类型：期中考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列各式中是二次根式的是（）

A、 $\sqrt[3]{8}$ B、 $\sqrt{- 1}$ C、﹣ $\sqrt{3}$ D、2

查看试题解析
2. 下列四组数据中，不能作为直角三角形三边长的是（）

A、5，12，13 B、1，2，3 C、9，40，41 D、3，4，5

查看试题解析
3. 使 $\sqrt{x - 3}$ 有意义的x的取值范围是（）

A、x≤3 B、x＜3 C、x≥3 D、x＞3

查看试题解析
4. 下列计算正确的是（）

A、 $\sqrt{2}$ + $\sqrt{3}$ ＝ $\sqrt{5}$ B、 $\sqrt{4 \times 2}$ ＝2 $\sqrt{2}$ C、 $\sqrt{6}$ +2＝ $\sqrt{3}$ D、3 $\sqrt{2}$ ﹣ $\sqrt{2}$ ＝3

查看试题解析
5. 在▱ABCD中，∠A＝50°，则∠C＝（）

A、130° B、50° C、40° D、25°

查看试题解析
6. 在四边形ABCD中，对角线AC，BD互相平分，要使四边形ABCD为矩形，需添加的条件是（）

A、∠A＝∠C B、AB＝BC C、AC⊥BD D、AC＝BD

查看试题解析
7. 如图，▱ABCD的对角线AC与BD相交于点O，AB⊥AC，若AB＝4，AC＝6，则BO的长为（）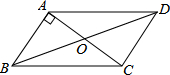

A、5 B、8 C、10 D、11

查看试题解析
8. 如图，菱形ABCD的边长为 $\sqrt{5}$ ，对角线AC，BD交于点O，OA＝1，则菱形ABCD的面积为（）

A、 $\sqrt{5}$ B、2 $\sqrt{5}$ C、2 D、4

查看试题解析
9. 如图是一个圆柱形饮料罐，底面半径是5，高是12，上底面中心有一个小圆孔，则一条到达底部的直吸管在罐内部分a的长度x（罐壁厚度和小圆孔大小忽略不计）范围是（）

A、12≤x≤13 B、12≤x≤15 C、5≤x≤12 D、5≤x≤13

查看试题解析
10. 如图，已知正方形ABCD的边长为12，BE＝EC，将正方形的边CD沿DE折叠到DF，延长EF交AB于G，连接DG．现有如下3个结论：①AG+EC＝GE；②∠GDE＝45°；③五边形DAGEC的周长是44，其中正确的个数为（）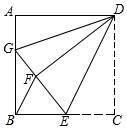

A、0 B、1 C、2 D、3

查看试题解析

二、填空题（每题3分，共18分）

11. 计算： $\sqrt{{(- 6)}^{2}}$ ＝．

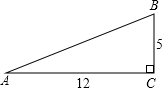
查看试题解析
12. 如果最简二次根式 $\sqrt{2 x + 1}$ 与 $\sqrt{5}$ 可以合并，则x＝．

查看试题解析
13. 如图，在Rt△ABC中，∠C＝90°，BC＝5，AC＝12，则AB＝，∠A＝， ∠B＝．（角度精确到1′）

查看试题解析
14. 如图，以正方形ABCD的一边AD为边向外作等边△ADE，则∠ABE的度数是．

查看试题解析
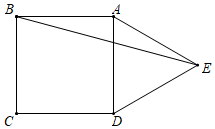15. 已知x＝ $2 - \sqrt{10}$ ，代数式x²﹣4x﹣6的值为．

查看试题解析
16. 如图，四边形ABCD中，∠A＝90°，AB＝2 $\sqrt{3}$ ，AD＝2，点M，N分别为线段BC，AB上的动点（含端点，但点M不与点B重合），点E，F分别为DM，MN的中点，则EF长度的最大值为．

查看试题解析

三、解答题（共72分）

17.

(1)、5 $\sqrt{3}$ ﹣ $\sqrt{8}$ ﹣ $\sqrt{27}$ ；

(2)、（4 $\sqrt{6}$ ﹣6 $\sqrt{2}$ ）+2 $\sqrt{2}$ ．

查看试题解析
18. （ $\sqrt{5}$ +2 $\sqrt{2}$ ）（ $\sqrt{5}$ ﹣2 $\sqrt{2}$ ）+（ $\sqrt{5}$ ﹣ $\sqrt{2}$ ）² ．

查看试题解析
19. 如图，在矩形ABCD中，E、F分别在AB、CD上，且AE＝CF．求证：四边形DEBF是平行四边形．

查看试题解析
20. 如图，将长为2.5米长的梯子AB斜靠在墙上，BE长0.7米．

(1)、求梯子上端到墙的底端E的距离（即AE的长）；

(2)、如果梯子的顶端A沿墙下滑0.4米（即AC＝0.4米），则梯脚B将外移（即BD长）多少米？

查看试题解析
21. 已知等腰三角形ABC的底边长BC＝20cm，D是AC上的一点，且BD＝16cm，CD＝12cm．

(1)、求证：BD⊥AC；

(2)、求△ABC的面积．

查看试题解析
22. 如图，在Rt△ABC中，∠BAC＝90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F．

(1)、求证：四边形ADCF是菱形；

(2)、若AC＝6，AB＝8，求菱形ADCF的面积．

查看试题解析
23. 阅读下面的问题：
$\frac{1}{\sqrt{2} + 1} = \frac{\sqrt{2} - 1}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} - 1$

$\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{\sqrt{3} - \sqrt{2}}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2}$ ；

$\frac{1}{2 + \sqrt{3}} = \frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})} = 2 - \sqrt{3}$

……

(1)、求 $\frac{1}{\sqrt{7} + \sqrt{6}}$ 与 $\frac{1}{\sqrt{7} - \sqrt{6}}$ 的值．

(2)、已知n是正整数，求 $\frac{1}{\sqrt{n + 1} + \sqrt{n}}$ 与 $\frac{1}{\sqrt{n + 1} - \sqrt{n}}$ 的值；

(3)、计算 $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + ...... + \frac{1}{\sqrt{99} + \sqrt{98}} + \frac{1}{\sqrt{100} + \sqrt{99}}$ ．

查看试题解析
24. 如图，在平面直角坐标系中，O为坐标原点，A点的坐标为（18，0），B点的坐标为（0，24）．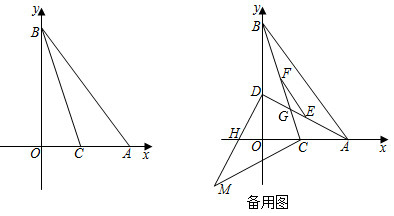

(1)、求AB的值；

(2)、点C在OA上，且BC平分∠OBA，求点C的坐标；

(3)、在（2）的条件下，点M在第三象限，点D为y轴上的一个点，连接DM交x轴于点H，连接CM，点F为BC的中点，点E为AD的中点，AD与BC交于点G，点H为DM的中点，当∠MCG﹣∠DGF＝∠OAB，且AD＝CM时，求线段EF的长．

查看试题解析
25. 如图，在平行四边形ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于F，以EC、CF为邻边作平行四边形ECFG，如图1所示．

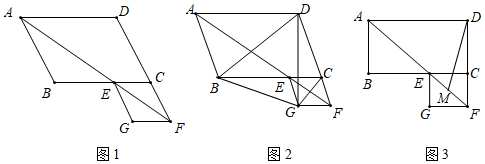(1)、证明平行四边形ECFG是菱形；

(2)、若∠ABC＝120°，连接BG、CG、DG，如图2所示，
①求证：△DGC≌△BGE；

②求∠BDG的度数；

(3)、若∠ABC＝90°，AB＝8，AD＝14，M是EF的中点，如图3所示，求DM的长．

查看试题解析