辽宁省沈阳市沈河区2020-2021学年七年级下学期数学期中试卷
试卷更新日期：2021-06-17 类型：期中考试
一、选择题（下列各题的备选答案中，只有一个答案是正确的，每小题2分，共20分）
-
1. 计算230的结果是（ ）A、23 B、1 C、0 D、322. 如图，下列说法正确的是（ ）
A、∠2与∠3是同旁内角 B、∠1与∠2是同位角 C、∠1与∠3是同位角 D、∠1与∠2是内错角3. 下列运算正确的是（ ）A、a5÷a2＝a3 B、a2•a3＝a6 C、3a2﹣2a＝a2 D、（a+b）2＝a2+b24. 下列各组线段能组成一个三角形的是（ ）A、2cm，3cm，6cm B、6cm，8cm，10cm C、5cm，5cm，10cm D、4cm，6cm，10cm5. 如图，某单位要在河岸l上建一个水泵房引水到C处，他们的做法是：过点C作CD⊥l于点D，将水泵房建在了D处．这样做最节省水管长度，其数学道理是（ ）
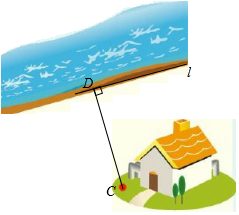A、两点之间，线段最短 B、在同一平面内，过一点有且只有一条直线与已知直线垂直 C、两点确定一条直线 D、直线外一点与直线上所有点的连线中，垂线段最短6. 华为麒麟990芯片采用了最新的0.000000007米的工艺制程，数0.000000007用科学记数法表示为（ ）A、7×10﹣9 B、7×10﹣8 C、0.7×10﹣9 D、0.7×10﹣87. 如果将一副三角板按如图方式叠放，那么∠1的度数是（ ）
A、90° B、100° C、105° D、135°8. 二十四节气是中国古代劳动人民长期经验积累的结晶，它与白昼时长密切相关，如图是一年中部分节气所对应的白昼时长示意图.则夏至与秋分白昼时长相差（ ）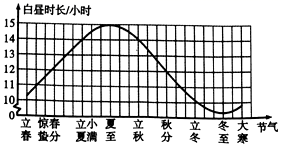
A、2小时 B、3小时 C、2.5小时 D、4小时9. 如图，在△ABC和△DEC中，已知AB＝DE，还需添加两个条件才能使△ABC≌△DEC，添加的一组条件错误的是（ ）
A、BC＝DC，∠A＝∠D B、BC＝EC，AC＝DC C、∠B＝∠E，∠BCE＝∠ACD D、BC＝EC，∠B＝∠E10. 研究表明，当每公顷钾肥和磷肥的施用量一定时，氮肥施用量与土豆的产量有如表所示的关系：氮肥施用量/千克
0
34
67
101
135
202
259
336
404
471
土豆产量/吨
15.18
21.36
25.72
32.29
34.05
39.45
43.15
43.46
40.83
30.75
下列说法错误的是（ ）
A、氮肥施用量是自变量，土豆产量是因变量 B、当氮肥的施用量是101千克/公顷时，土豆的产量是32.29吨/公顷 C、如果不施氮肥，土豆的产量是15.18吨/公顷 D、氮肥施用量404千克/公顷比氮肥施用量336千克/公顷时的土豆的产量更高二、填空题（每小题3分，共18分）
-
11. 已知am＝3，an＝2，则am+n＝.12. 如图，一张宽度相等的长方形纸条，如图所示折叠一下，那么∠1＝°．
13. 将长为23cm、宽为10cm的长方形白纸，按如图所示的方法粘合起来，粘合部分的宽为2cm，设x张白纸粘合后的总长度为ycm，y与x的函数关系式为 ．
14. 如图，在△ABC中，∠BAC＝100°，AD⊥BC于D点，AE平分∠BAC交BC于点E．若∠C＝26°，则∠DAE的度数为 ．
15. 如图的瓶子中盛满了水，则水的体积是 ． （用代数式表示）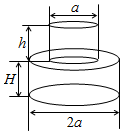
16. 如图，∠CAD和∠CBD的平分线相交于点P．请写出∠C、∠D、∠P的数量关系 ．
三、解答题（第17小题16分，18小题6分，19小题6分，20小题8分，共36分）
-
17. 计算：(1)、（﹣3）0﹣2×23﹣ ；(2)、（﹣2a）3﹣（﹣a）•（3a）2；(3)、（x+1）（2x﹣3）；(4)、199×201+1．（利用乘法公式）18. 先化简，再求值：[（2x+y）（2x﹣y）﹣（2x﹣y）2]÷2y，其中x＝﹣1，y＝2．19. 如图，在△ABC中，D是AB边上的一点．请用尺规作图法，在△ABC内，作出∠ADE，使∠ADE＝∠B，DE交AC于点E．（保留作图痕迹不写作法）
20. 完成推理填空如图，已知∠B＝∠D，∠BAE＝∠E．将证明∠AFC+∠DAE＝180°的过程填写完整．
证明：∵∠BAE＝∠E，
∴ ▲ ∥ ▲ （ ）．
∴∠B＝∠ ▲ （ ）．
又∵∠B＝∠D，
∴∠D＝∠ ▲ （等量代换）．
∴AD∥BC（ ）．
∴∠AFC+∠DAE＝180°（ ）．
四、（本题8分）
-
21. 如图，BE⊥AE，CF⊥AE，垂足分别为E、F，D是EF的中点，CF＝AF．
(1)、请说明CD＝BD；(2)、若BE＝6，DE＝3，请直接写出△ACD的面积．五、（本题8分）
-
22. 小明家距离学校8千米．一天早晨，小明骑车上学途中自行车出现故障，他于原地修车，车修好后，立即在确保安全的前提下以更快的速度匀速骑行到达学校．如图反映的是小明上学过程中骑行的路程（千米）与他所用的时间（分钟）之间的关系，请根据图象，解答下列问题：
(1)、小明骑行了千米时，自行车出现故障；修车用了分钟；(2)、自行车出现故障前小明骑行的平均速度为千米/分，修好车后骑行的平均速度为千米/分；(3)、若自行车不发生故障，小明一直按故障前的速度匀速骑行，与他实际所用时间相比，将早到或晚到学校多少分钟？六、（本题8分）
-
23. 劳动是财富的源泉，也是幸福的源泉．沈河区某中学对劳动教育进行积极探索和实践，创建学生劳动教育基地，让学生参与农耕劳作．如图，现计划利用校园围墙的一段MN（MN最长可用25m），用40m长的篱笆，围成一个长方形菜园ABCD．设AB的长为xm（7.2≤x＞20）．
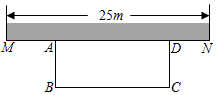(1)、BC的长度为 m（用含x的代数式表示），长方形菜园的面积S（m2）与AB的长x（m）的关系式为S＝ ；(2)、根据（1）中的关系式完成如表：AB的长x（m）
8
9
10
11
12
13
14
15
……
菜园的面积S（m2）
192
198
182
168
150
……
(3)、请根据表中数据分析，S如何随x的变化而变化？（写出一个结论即可）七、（本题10分）
-
24. 我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”（如图所示）就是一例．
这个三角形的构造法则为：两腰上的数都是1，其余每个数均为其上方（左右）两数之和．事实上，这个三角形给出了（a+b）n（n为正整数）的展开式（按a的次数由大到小的顺序排列）的系数规律．例如，在三角形中第三行的三个数1、2、1，恰好对应（a+b）2＝a2+2ab+b2展开式中各项的系数；第四行的四个数1、3、3、1，恰好对应着（a+b）3＝a3+3a2b+3ab2+b3展开式中各项的系数等等．
(1)、根据上面的规律，（a+b）4展开式的各项系数中最大的数为 ；(2)、求出25+5×24×（﹣3）+10×23×（﹣3）2+10×22×（﹣3）3+5×2×（﹣3）4+（﹣3）5的值；(3)、若（x﹣1）2020＝a1x2020+a2x2019+a3x2018+……+a2019x2+a2020x+a2021 ， 求出a1+a2+a3+……+a2019+a2020的值．八、（本题12分）
-
25. 已知直线MN∥PQ，点A在直线MN上，点B、C为平面内两点，AC⊥BC于点C．
(1)、如图1，当点B在直线MN上，点C在直线MN上方时，延长CB交直线PQ于点D，则∠CAB和∠CDP之间的数量关系是 ．(2)、如图2，当点C在直线MN上且在点A左侧，点B在直线MN与PQ之间时，过点B作BD⊥AB交直线PQ于点D．为探究∠ABC与∠BDP之间的数量关系，小明过点B作BF∥MN．请根据他的思路，写出∠ABC与∠BDP的关系，并说明理由；(3)、如图3，在（2）的条件下，作∠ABD的平分线交直线MN于点E，当∠AEB＝2∠ABC时，直接写出∠ABC的度数．(4)、如图4，当点C在直线MN上且在点A左侧，点B在直线PQ下方时，过点B作BD⊥AB交直线PQ于点D．作∠ABD的平分线交直线MN于点E，当∠BDP＝2∠BEN时，请补充图形并直接写出∠ABC的度数．
-
-
-
-