四川省自贡市2021年中考数学试卷
试卷更新日期:2021-06-17 类型:中考真卷
一、选择题(共12个小题,每小题4分,共48分)
-
1. 自贡恐龙博物馆是世界三大恐龙遗址博物馆之一.今年“五一黄金周”共接待游客8.87万人次,人数88700用科学记数法表示为( )A、0.887×105 B、8.87×103 C、8.87×104 D、88.7×1032. 如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“迎”字一面的相对面上的字是( )
 A、百 B、党 C、年 D、喜3. 下列运算正确的是( )A、5a2﹣4a2=1 B、(﹣a2b3)2=a4b6 C、a9÷a3=a3 D、(a﹣2b)2=a2﹣4b24. 下列图形中,是轴对称图形且对称轴条数最多的是( )A、
A、百 B、党 C、年 D、喜3. 下列运算正确的是( )A、5a2﹣4a2=1 B、(﹣a2b3)2=a4b6 C、a9÷a3=a3 D、(a﹣2b)2=a2﹣4b24. 下列图形中,是轴对称图形且对称轴条数最多的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,AC是正五边形ABCDE的对角线,∠ACD的度数是( )
5. 如图,AC是正五边形ABCDE的对角线,∠ACD的度数是( )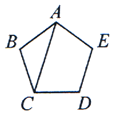 A、72° B、36° C、74° D、88°6. 学校为了解“阳光体育”活动开展情况,随机调查了50名学生一周参加体育锻炼时间,数据如下表所示:
A、72° B、36° C、74° D、88°6. 学校为了解“阳光体育”活动开展情况,随机调查了50名学生一周参加体育锻炼时间,数据如下表所示:人数(人)
9
16
14
11
时间(小时)
7
8
9
10
这些学生一周参加体育锻炼时间的众数、中位数分别是( )
A、16,15 B、11,15 C、8,8.5 D、8,97. 已知x2﹣3x﹣12=0,则代数式﹣3x2+9x+5的值是( )A、31 B、﹣31 C、41 D、﹣418. 如图,A(8,0),C(﹣2,0),以点A为圆心,AC长为半径画弧,交y轴正半轴于点B,则点B的坐标为( )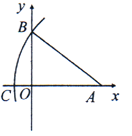 A、(0,5) B、(5,0) C、(6,0) D、(0,6)9. 已知蓄电池的电压为定值,使用蓄电池时,电流O(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
A、(0,5) B、(5,0) C、(6,0) D、(0,6)9. 已知蓄电池的电压为定值,使用蓄电池时,电流O(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.下列说法正确的是( )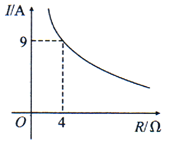 A、函数解析式为I= B、蓄电池的电压是18V C、当I≤10A时,R≥3.6Ω D、当R=6Ω时,I=4A10. 如图,AB为⊙O的直径,弦CD⊥AB于点F,OE⊥AC于点E,若OE=3,OB=5,则CD的长度是( )
A、函数解析式为I= B、蓄电池的电压是18V C、当I≤10A时,R≥3.6Ω D、当R=6Ω时,I=4A10. 如图,AB为⊙O的直径,弦CD⊥AB于点F,OE⊥AC于点E,若OE=3,OB=5,则CD的长度是( )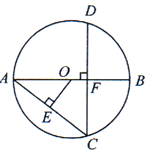 A、9.6 B、4 C、5 D、1011. 如图,在正方形ABCD中,AB=6,M是AD边上的一点,AM:MD=1:2.将△BMA沿BM对折至△BMN,连接DN,则DN的长是( )
A、9.6 B、4 C、5 D、1011. 如图,在正方形ABCD中,AB=6,M是AD边上的一点,AM:MD=1:2.将△BMA沿BM对折至△BMN,连接DN,则DN的长是( ) A、 B、 C、3 D、12. 如图,直线y=﹣2x+2与坐标轴交于A、B两点,点P是线段AB上的一个动点,过点P作y轴的平行线交直线y=﹣x+3于点Q,△OPQ绕点O顺时针旋转45°,边PQ扫过区域(阴影部分)面积的最大值是( )
A、 B、 C、3 D、12. 如图,直线y=﹣2x+2与坐标轴交于A、B两点,点P是线段AB上的一个动点,过点P作y轴的平行线交直线y=﹣x+3于点Q,△OPQ绕点O顺时针旋转45°,边PQ扫过区域(阴影部分)面积的最大值是( )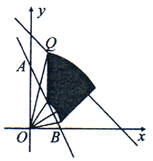 A、 π B、 π C、 π D、 π
A、 π B、 π C、 π D、 π二、填空题(共6个小题,每小题4分,共24分)
-
13. 请写出一个满足不等式x+ >7的整数解.14. 某中学规定学生的学期体育成绩满分为100,其中体育课外活动占30%,期末考试成绩占70%,小彤的这两项成绩依次是90,80.则小彤这学期的体育成绩是.15. 化简: ﹣ =.16. 如图,某学校“桃李餐厅”把WIFI密码做成了数学题.小红在餐厅就餐时,思索了一会儿,输入密码,顺利地连接到了“桃李餐厅”的网络.那么她输入的密码是.
 17. 当自变量﹣1≤x≤3时,函数y=|x﹣k|(k为常数)的最小值为k+3,则满足条件的k的值为.
17. 当自变量﹣1≤x≤3时,函数y=|x﹣k|(k为常数)的最小值为k+3,则满足条件的k的值为.三、解答题
-
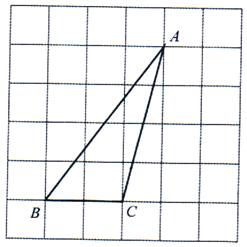
18. 如图,△ABC的顶点均在正方形网格格点上.只用不带刻度的直尺,作出△ABC的角平分线BD(不写作法,保留作图痕迹).
 19. 计算: ﹣|﹣7|+(2﹣ )0.20. 如图,在矩形ABCD中,E,F分别是AB,CD的中点.求证:DE=BF.
19. 计算: ﹣|﹣7|+(2﹣ )0.20. 如图,在矩形ABCD中,E,F分别是AB,CD的中点.求证:DE=BF.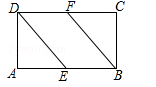 21. 在一次数学课外实践活动中,小明所在的学习小组从综合楼顶部B处测得办公楼底部D处的俯角是53°,从综合楼底部A处测得办公楼顶部C处的仰角恰好是30°,综合楼高24米.请你帮小明求出办公楼的高度.(结果精确到0.1,参考数据tan37°≈0.75,tan53°≈1.33, ≈1.73)
21. 在一次数学课外实践活动中,小明所在的学习小组从综合楼顶部B处测得办公楼底部D处的俯角是53°,从综合楼底部A处测得办公楼顶部C处的仰角恰好是30°,综合楼高24米.请你帮小明求出办公楼的高度.(结果精确到0.1,参考数据tan37°≈0.75,tan53°≈1.33, ≈1.73)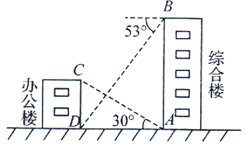 22. 随着我国科技事业的不断发展,国产无人机大量进入快递行业.现有A,B两种型号的无人机都被用来运送快件,A型机比B型机平均每小时多运送20件,A型机运送700件所用时间与B型机运送500件所用时间相等,两种无人机平均每小时分别运送多少快件?23. 为了弘扬爱国主义精神,某校组织了“共和国成就”知识竞赛,将成绩分为:A(优秀)、B(良好)、C(合格)、D(不合格)四个等级.小李随机调查了部分同学的竞赛成绩,绘制了如下统计图.
22. 随着我国科技事业的不断发展,国产无人机大量进入快递行业.现有A,B两种型号的无人机都被用来运送快件,A型机比B型机平均每小时多运送20件,A型机运送700件所用时间与B型机运送500件所用时间相等,两种无人机平均每小时分别运送多少快件?23. 为了弘扬爱国主义精神,某校组织了“共和国成就”知识竞赛,将成绩分为:A(优秀)、B(良好)、C(合格)、D(不合格)四个等级.小李随机调查了部分同学的竞赛成绩,绘制了如下统计图.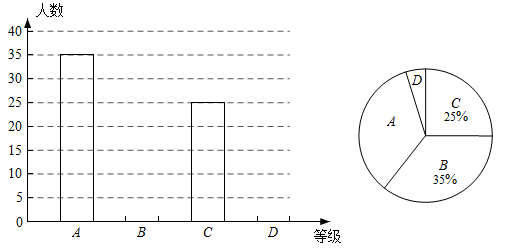 (1)、本次抽样调查的样本容量是 ▲ , 请补全条形统计图;(2)、已知调查对象中只有两位女生竞赛成绩不合格,小李准备随机回访两位竞赛成绩不合格的同学,请用树状图或列表法求出恰好回访到一男一女的概率;(3)、该校共有2000名学生,请你估计该校竞赛成绩“优秀”的学生人数.24. 函数图象是研究函数的重要工具.探究函数性质时,我们经历了列表、描点、连线画出函数图象,然后观察分析图象特征,概括函数性质的过程.请结合已有的学习经验,画出函数y=﹣ 的图象,并探究其性质.
(1)、本次抽样调查的样本容量是 ▲ , 请补全条形统计图;(2)、已知调查对象中只有两位女生竞赛成绩不合格,小李准备随机回访两位竞赛成绩不合格的同学,请用树状图或列表法求出恰好回访到一男一女的概率;(3)、该校共有2000名学生,请你估计该校竞赛成绩“优秀”的学生人数.24. 函数图象是研究函数的重要工具.探究函数性质时,我们经历了列表、描点、连线画出函数图象,然后观察分析图象特征,概括函数性质的过程.请结合已有的学习经验,画出函数y=﹣ 的图象,并探究其性质.列表如下:
x
…
﹣4
﹣3
﹣2
﹣1
0
1
2
3
4
…
y
…
a
0
b
﹣2
﹣
﹣
…
(1)、直接写出表中a、b的值,并在平面直角坐标系中画出该函数的图象;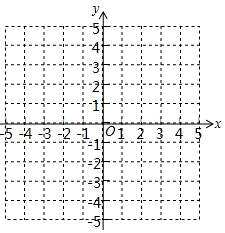 (2)、观察函数y=﹣ 的图象,判断下列关于该函数性质的命题:
(2)、观察函数y=﹣ 的图象,判断下列关于该函数性质的命题:①当﹣2≤x≤2时,函数图象关于直线y=x对称;
②x=2时,函数有最小值,最小值为﹣2;
③﹣1<x<1时,函数y的值随x的增大而减小.
其中正确的是.(请写出所有正确命题的番号)
(3)、结合图象,请直接写出不等式 >x的解集.25. 如图,点D在以AB为直径的⊙O上,过D作⊙O的切线交AB延长线于点C,AE⊥CD于点E,交⊙O于点F,连接AD,FD.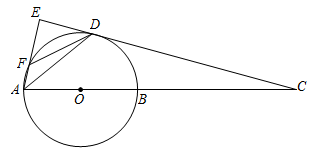 (1)、求证:∠DAE=∠DAC;(2)、求证:DF•AC=AD•DC;(3)、若sin∠C= ,AD=4 ,求EF的长.26. 如图,抛物线y=(x+1)(x﹣a)(其中a>1)与x轴交于A、B两点,交y轴于点C.
(1)、求证:∠DAE=∠DAC;(2)、求证:DF•AC=AD•DC;(3)、若sin∠C= ,AD=4 ,求EF的长.26. 如图,抛物线y=(x+1)(x﹣a)(其中a>1)与x轴交于A、B两点,交y轴于点C. (1)、直接写出∠OCA的度数和线段AB的长(用a表示);(2)、若点D为△ABC的外心,且△BCD与△ACO的周长之比为 :4,求此抛物线的解析式;(3)、在(2)的前提下,试探究抛物线y=(x+1)(x﹣a)上是否存在一点P,使得∠CAP=∠DBA?若存在,求出点P的坐标;若不存在,请说明理由.
(1)、直接写出∠OCA的度数和线段AB的长(用a表示);(2)、若点D为△ABC的外心,且△BCD与△ACO的周长之比为 :4,求此抛物线的解析式;(3)、在(2)的前提下,试探究抛物线y=(x+1)(x﹣a)上是否存在一点P,使得∠CAP=∠DBA?若存在,求出点P的坐标;若不存在,请说明理由.